Definition af en metrik – det abstrakte afstandsbegreb
Man har ikke frit valg til at bestemme, hvad man vil bruge som afstandsmål. Hvis det skal give mening, skal man have en metrik – det betyder, at afstanden skal opfylde nogle betingelser:
En metrik på en mængde \(M\) er en funktion \(d\) fra \(M\times M\) til \(\mathbb{R}\) – altså en funktion, som tager to elementer i \(M\) og giver et reelt tal.
Hvis en funktion \(d\) skal være en metrik, så vil vi kræve, at den opfylder følgende fire betingelser:
For alle \(p,q,r\) i \(M\) skal der gælde, at
\(d(p,q)\geq 0\). Med ord: Alle afstande er positive eller \(0\).
\(d(p,p)=0\) og \(d(p,q)=0\) hvis og kun hvis \(p=q\). Med ord: Afstanden fra et punkt til sig selv er \(0\), og ingen andre afstande er \(0\).
\(d(p,q)=d(q,p)\). Det vil sige, at afstanden er symmetrisk. Med ord: Der er lige så langt fra \(p\) til \(q\) som fra \(q\) til \(p\).
\(d(p,q)+d(q,r)\geq d(p,r)\). Det kaldes for trekantsuligheden. Med ord: Der er mindst lige så langt fra \(p\) til \(r\) via \(q\), som direkte fra \(p\) til \(r\).
Lad os tage et velkendt eksempel.
Eksempel 1 (Euklidisk afstand som metrik) Lad \(M\) være alle punkter i planen og lad metrikken være den euklidiske afstand, som vi kender. Funktionen \(d\) vil så tage to punkter \(P(x_1,y_1)\) og \(Q(x_2,y_2)\) i planen og give et reelt tal som output svarende til den euklidiske afstand mellem \(P\) og \(Q\). Det vil sige, at \[ d(P,Q) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\] Vi vil senere vise, at denne funktion opfylder betingelserne for en metrik, som defineret ovenfor.
Det er en meget kort definition. Og meget, meget generel. \(M\) er en mængde - der er en strengt logisk måde at gå til mængder på, men lad os her sige en samling af objekter, som vi også kalder elementer af mængden. Læg mærke til, at vi her bare graver problemet lidt længere ned i sandet – fejer det ind under gulvtæppet – for hvad er "objekter"? Det kommer vi ikke nærmere her.
Det er ret nemt at acceptere, at de tre krav er rimelige. Men er det nok? Og er det nu alligevel rimeligt? Hvad med symmetrien? Der er vel længere \(10\) km op ad bakke end \(10\) km ned ad bakke, hvis man tænker på arbejdsindsats. Så måske giver det ikke altid mening?1
1 Hvis funktionen \(d\) opfylder 1,2,4, er det en quasimetrik. Opfylder den 1,2,3, er det en semimetrik. Opfylder den 1, 3 og 4, og første del af 2 (\(d(p,p)=0\), men der kan være andre afstande, der er \(0\)) er det en pseudometrik. Der findes såmænd også præmetrikker, metametrikker, pseudoquasimetrikker og sikkert andre – "falske metrikker".
2 Ordet "rum" skal man ikke lægge for meget i. Der er ikke anden information i det end definitionen. Intuition skal man være varsom med.
Definitionen af metrik som her, er den, vi bruger i matematik. Den har vist sig nyttig. Der er en skov af artikler og bøger, hvor man kan se, hvad man ved, når man har en metrik. En mængde med en metrik kaldes et metrisk rum.2
Eksempel 2 (Den diskrete metrik) På en mængde \(M\) er funktionen \(d\) givet ved.
\(d(p,p)=0\)
Hvis \(p\neq q\) er \(d(p,q)=1\).
Det er en metrik – den opfylder definitionen ovenfor. Men det er ikke nogen specielt nyttig metrik. Alle elementer ligger lige tæt på alle andre, så der er ikke ny information – udover, om to elementer er ens eller ej.
Eksempel 3 (Euklidisk afstand som metrik, fortsat) Vi vil vise, at den euklidiske afstand mellem to punkter rent faktisk opfylder betingelserne for en metrik, som vi definerede dem ovenfor:
Den første betingelse er opfyldt, da \[d(P,Q)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \geq 0\]
I den anden betingelse er der to ting at vise. For det første ses det nemt, at \[d(P,P)=\sqrt{(x_1-x_1)^2+(y_1-y_1)^2} = \sqrt{0}=0\] For det andet – hvis \[d(P,Q)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=0\] så kan det kun lade sig gøre, hvis både \[(x_2-x_1)^2=0 \quad \textrm{og} \quad (y_2-y_1)^2=0\] Det kan igen kun lade sig gøre3, hvis \[x_1=x_2 \quad \textrm{og} \quad y_1=y_2\] Det vil sige, at \(P=Q\), og den anden betingelse er således også opfyldt.
Da \((a-b)^2=(b-a)^2\) får vi, at \[d(P,Q)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=d(Q,P)\] og den tredje betingelse er opfyldt.
Det kræver lidt mere at bevise trekantsuligheden, men intuitivt virker det fornuftigt nok. Hvis du i trekant \(PQR\), skal fra \(P\) til \(R\), så bliver turen dertil ikke kortere, hvis du først går om \(Q\).
3 Brug nulreglen.
Eksempel 4 (Ikke-metrik) En elev er træt af kvadratrødder og tænker, at man vel kan droppe den euklidiske afstand og i stedet definere en afstand mellem to punkter \(p(x_1,y_1)\) og \(q(x_2,y_2)\) i planen som følger:
\[D(p,q)=(x_2-x_1)^2+(y_2-y_1)^2 \tag{1}\]
Der er bare et lille problem: \(D\) er ikke en metrik! Den opfylder nemlig ikke trekantsuligheden. Men hvordan kan man se det? Husk på, at vi bare skal finde ét eksempel – det vil sige tre punkter \(p,q,r\), hvor trekantsuligheden ikke holder. Så har vi vist, at \(D\) ikke er en metrik.
Et konkret eksempel: \(p=(0,0)\), \(q=(2,0)\), \(r=(4,0)\). Se figur 1.
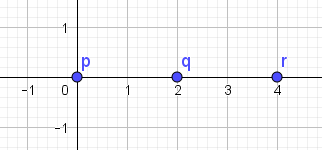
Afstanden fra \(p\) til \(r\) er \(D(p,r)=4^2+0^2=16\), mens afstanden fra \(p\) til \(q\) er \(D(p,q)=2^2+0^2=4\) og det samme gælder afstanden fra \(q\) til \(r\): \(D(q,r)=2^2+0^2=4\) så \[D(p,q)+D(q,r)=8\] mens \[D(p,r)=16\] Altså er \[ D(p,q)+D(q,r) \ngeq D(p,r) \]
Et andet eksempel, som ligner en rigtig trekant: \(p=(0,0)\) \(q=(2,1)\), \(r=(4,0)\). Se figur 2.
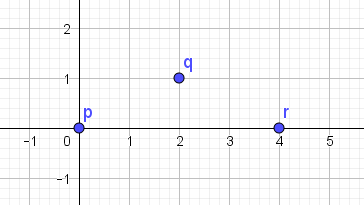
Her er \(D(p,q)=2^2+1^2=5\) og \(D(q,r)=(4-2)^2+1^2=5\) så \[D(p,q)+D(q,r)=10\] mens \[D(p,r)=4^2+0^2=16\] Igen er det med dette afstandsmål kortere at gå fra \(p\) til \(r\) via \(q\) end at gå direkte. Og det er altså derfor ikke en metrik.