Anbefalet til dig
Du kender det sikkert. Du har lige siddet og set en film på Netflix. Bagefter får du vist et forslag til en ny film, du kan se. Du har da egentlig også altid gerne villet se "Mission: Impossible", så du klikker på filmen. Efter den kommer der nye forslag. Før du får set dig om, har du siddet oppe hele natten og set film. Ikke så godt for dig, hvis du skal op og i skole næste dag, men godt for Netflix. Men hvordan ved Netflix egentlig, hvilke film der kan friste dig til at se videre? Jo, de har indsamlet data om, hvilke film du og andre brugere har set. Ved hjælp af en algoritme, et såkaldt anbefalingssystem, prøver den at forudsige, hvilken film du vil kunne lide.
Du kender anbefalingssystemer fra mange andre onlinetjenester, for eksempel YouTubes videoforslag og Spotifys personlige playlister. Sociale medier som Facebook bruger blandt andet algoritmerne til at foreslå venner og grupper. Og så kender du dem nok også fra onlinehandel. Når du har købt en vare på nettet, foreslår forretningen dig som regel en liste med andre varer, du kunne være interesseret i. Anbefalingerne er en service, der gør det nemmere at finde relevant indhold, men samtidig har de til formål at maksimere den tid, du bruger på en onlinetjeneste, eller de penge, du bruger hos en onlinebutik. Fælles for alle de bagvedliggende virksomheder er, at anbefalingssystemerne er afgørende for deres succes.
I denne note skal vi se på, hvordan anbefalingssystemer er lavet. Der er to overordnede typer af anbefalingssystemer:
- Samarbejdsbaseret:1 Her sammenligner man brugerens adfærd med andre brugere. Algoritmen vil så anbefale noget, som brugere med samme adfærd som dig kan lide. I Netflix-eksemplet kunne algoritmen for eksempel kigge på de brugere, der har set de samme film som dig. Hvis mange af dem også har set "Mission: Impossible", tyder det på, at brugere, der ligner dig, kan lide den, og du vil derfor blive anbefalet at se den.
1 Engelsk: Collaborative filtering.
- Indholdsbaseret:2 Her laver man en brugerprofil for hver bruger, der beskriver, hvilken type indhold, brugeren godt kan lide. Algoritmen kan så foreslå mere indhold af samme type. Hvis du har set mange actionfilm på Netflix, vil din brugerprofil fortælle, at du er glad for actionfilm, og algoritmen vil så foreslå actionfilmen "Mission: Impossible".
2 Engelsk: Content based filtering.
Vi skal se simple eksempler på begge typer algoritmer. Der vil undervejs være links til mere avancerede algoritmer, der kan bruges til at forbedre dem. Fordi anbefalingssystemerne er så vigtige for onlinevirksomhederne, bruger de mange ressourcer på at forfine og videreudvikle algoritmerne, og de præcise algoritmer, der bruges i dag, er typisk en forretningshemmelighed!
En samarbejdsbaseret algoritme
Vi ser først et eksempel på, hvordan man kan lave samarbejdsbaserede anbefalinger. Vi forestiller os derfor en filmstreamingtjeneste, der gerne vil lave anbefalinger af typen "Andre har også set…". De vil altså gerne foreslå dig film, som brugere, der ligner dig, godt kan lide.
Lad os sige, at tjenesten har et katalog bestående af \(p\) film. For hver bruger registrerer hjemmesiden, hvilke film brugeren har set. Hvis tjenesten har \(n\) kunder, så indsamler den et datasæt som illustreret i tabel 1. Hver række svarer til en bruger, og hver søjle svarer til en film. Et 1-tal betyder, at brugeren har set filmen, og et 0 angiver, at brugeren ikke har set filmen.
| Brugernummer | "Blinkende lygter" | "Olsen-banden" | "Hævnen" |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 |
Hyppige filmkombinationer
Som det første vil vi gerne finde ud af, hvilke film der typisk bliver set af den samme bruger. Lad os kalde filmene i tjenestens katalog for \(f_1,\ldots,f_p\). Vi kigger så på en delmængde \(J\subseteq \{f_1,\ldots,f_p \}\) af filmene. Lad \(F_J\) angive hændelsen, at en bruger har set alle filmene i \(J\). Sandsynligheden for, at brugeren har set alle film i \(J\), er givet ved: \[ P(F_J)= P(\text{ En bruger har set alle film i } J) \]
Vi kan estimere \(P(F_J)\) ved frekvensen \(\hat{P}(F_{J})\), som er andelen af brugerne, der har set alle film i \(J\). \[ \begin{aligned} \hat{P}(F_J) &= \frac{\text{Antal brugere der så alle film i } J}{\text{Samlet antal brugere}}\\ &= \frac{\text{Antal brugere der så alle film i } J}{n} \end{aligned} \tag{1}\] Populære filmkombinationer vil have høj frekvens.
Eksempel 1 En streamingtjeneste viser filmene "Titanic" og "Mission: Impossible". Hvis tjenesten har 1000 brugere, hvoraf 411 har set "Titanic", 358 har set "Mission: Impossible" og 198 har set både "Titanic" og "Mission: Impossible", så er \[ \begin{aligned} &\hat{P}(F_{\{\text{Titanic}\}}) = \frac{411}{1000}=0.411\\ &\hat{P}(F_{\{\text{Mission: Impossible}\}}) = \frac{358}{1000}=0.358\\ &\hat{P}(F_{\{\text{Titanic, Mission: Impossible}\}}) = \frac{198}{1000}=0.198 \end{aligned} \] "Titanic" var altså den mest populære af de to film, idet \(41.1\%\) af brugerne havde set den, mens kun \(35.5\%\) havde set "Mission: Impossible".
Andre har også set…
Streamingtjenesten har registreret, at du har set alle filmene i mængden \(I\). De vil nu gerne kunne udtale sig om, hvor sandsynligt det er, at du også vil se filmene i mængden \(J\). Vi antager, at mængderne \({I}\) og \({J}\) er disjunkte, altså at de ikke har nogen film tilfælles. Sandsynligheden for at se alle filmene i \(J\), givet at man har set alle filmene i \(I\), kan beskrives ved en betinget sandsynlighed.3 \[ P(F_{J}\mid F_{I}) = \frac{P(F_{I}\cap F_{J})}{P(F_{I})} \] Fælleshændelsen \(F_I \cap F_J\) er hændelsen, at man har set alle filmene i \(I\) og alle filmene i \(J\). Det vil sige, at man har set alle filmene i \(I\cup J\). Derfor er \(F_{I}\cap F_{J} = F_{I\cup J}\) og dermed \[ \frac{P(F_{J}\cap F_{I})}{P(F_{I})}=\frac{P(F_{I\cup J} )}{P(F_{I})} \tag{2}\]
3 Hvis du har brug for at genopfriske betingede sandsynligheder, kan du læse mere i boksen nedenfor.
Vi kan altså estimere sandsynligheden for, at en bruger, der har set alle film i \(I\), også har set alle film i \(J\), ved andelen af de brugere, der har set alle filmene i \(I\), der har set alle filmene i både \(I\) og \(J\).
Streamingtjenesten kan bruge disse betingede sandsynligheder til at foreslå nye film. Hvis de har registreret, at du har set alle film i \(I\), vil de foreslå en ny liste af film \(J\), hvor \(\hat{P}(F_J \mid F_I)\) er høj.
Man kan estimere sandsynligheden (2) ved at indsætte estimaterne for tæller og nævner fra (1). Det giver \[ \hat{P}(F_J\mid F_I) = \frac{\hat{P}(F_{{I} \cup {J}})}{\hat{P}(F_{I})}. \tag{3}\] I beregninger er det nyttigt at vide at \[ \begin{aligned} \hat{P}(F_J \mid F_I) &= \frac{\hat{P}(F_{I\cup J})}{\hat{P}(F_{I})}\\ &=\frac{\frac{\text{Antal der har set alle film i } I\cup J}{n}}{\frac{\text{Antal der har set alle film i } I }{n}}\\ &=\frac{\text{Antal der har set alle film i } I \cup J}{\text{Antal der har set alle film i } I} \end{aligned} \]
Eksempel 2 Vi ser igen på filmtjenesten fra eksempel 1. En bruger har lige set "Titanic", og filmtjenesten vil nu gerne anbefale en ny film. Vi ser derfor på sandsynligheden for, at en bruger, der har set "Titanic", også har set "Mission: Impossible". Vi finder \[\hat{P}(F_{\text{Mission: Impossible}} \mid F_{\text{ Titanic }} ) = \frac{198}{411} \approx 0.482\] Det er altså cirka 48,2% af de brugere, der har set "Titanic", der også har set "Mission: Impossible". Hvis der er 145 brugere, der både har set "Titanic" og "Jurassic Park", så er \[\hat{P}(F_{\text{ Jurassic Park}} \mid F_{\text{ Titanic }}) = \frac{145}{411} \approx 0.353 \] Folk, der har set "Titanic", er således mere tilbøjelige til at se "Mission: Impossible" end "Jurassic Park". "Mission: Impossible" vil derfor være den bedste anbefaling.
Begrænsninger ved algoritmen
Vi har beskrevet en simpel og klassisk måde at lave anbefalinger på, og er særligt relevant for onlineforretninger, som vil lave forslag af typen "Andre har også købt". Selv for en lille virksomhed er det nemt at indsamle det relevante data og bruge algoritmen til at lave nye forslag.
Der er dog også forskellige begrænsninger ved tilgangen ovenfor. Måske er der ingen brugere, der har set præcis de samme film som dig. I så fald har vi ikke nogen at sammenligne med. At man har set en film betyder jo heller ikke nødvendigvis, at man kunne lide den.
Moderne internetvirksomheder har mulighed for at indsamle meget mere data, som kan bruges til at forbedre anbefalingerne. Netflix indsamler for eksempel data om:
Filmene: For eksempel genre, sprog, instruktør, skuespillere, antal Oscars.
Brugeren: Ofte angiver man enkelte peronoplysninger, så som emailadresse og sprog, når man opretter en profil, men mange har ikke lyst til direkte at afgive for mange oplysninger om sig selv. I stedet prøver tjenesten at opnå disse oplysninger indirekte, ved at indsamle data om brugerens adfærd på deres hjemmeside.
Brugerens adfærd: Hvilke film har brugeren set, blev filmen set til ende, hvilken rating fik den efterfølgende, på hvilken tid af dagen blev filmen set og fra hvilket device, og hvilke film har brugeren ellers søgt på.
For at tage alle disse oplysninger i betragtning, får man brug for meget mere komplicerede algoritmer.
En indholdsbaseret algoritme
En af de ting, Netflix gør for at få flere oplysninger om din filmsmag, er, at de beder dig rate de film, du har set. I dag sker det med likes, men tidligere brugte de ratings fra 1 til 5. I det følgende antager vi, at alle ratings er på en skala fra 1 til 5, hvor 5 er bedst. Netflix bruger dine ratings til at prøve at gætte, hvordan du ville rate deres øvrige film. De kan så foreslå en film, som de tror, du vil rate højt.
I dette afsnit skal vi se på en indholdsbaseret tilgang til at forudsige, eller prædiktere, ratings. Idéen er, at dine ratings formodes at afhænge dels af egenskaber ved filmen, kaldet features, og dels af dine egne præferencer, det vil sige, hvor positivt eller negativt du vurderer forskellige features.
Multipel lineær regression
Som eksempel kan vi kigge på to features. Den første er, hvor mange procent af filmen, der udgøres af kærlighedsscener. Den kalder vi \(x_1\). Den anden er, hvor mange procent af filmen, der udgøres af actionscener. Den kalder vi \(x_2\). Begge features måles på en skala fra 0 til 100 procent. Vi prædikterer så en given brugers ratings ved modellen \[ \hat{r}=b + p_1x_1 + p_2x_2, \tag{4}\] Her er \(\hat{r}\) den prædikterede rating.4 Der indgår tre konstanter \(b\), \(p_1\) og \(p_2\) kaldet vægte5, som afhænger af den specifikke bruger.
4 Hatten over \(r\)’et angiver, at det er en prædikteret værdi, mens et \(r\) uden hat betegner brugerens faktiske rating.
5 Nogle gange kaldes de også for parametre.
Eksempel 3 En bruger har vægtene \(b=2\), \(p_1=-0.02\) og \(p_2=0.05\). Brugerens ratings prædikteres derfor ved \[\hat{r}= 2 - 0.02x_1 + 0.05x_2\] En romantisk film har måske \(x_1=50\) og \(x_2=0\). Vi forventer så, at brugeren ville give filmen ratingen \[\hat{r}=2-0.02\cdot 50+0.05\cdot 0=1\] En actionfilm ville måske have \(x_1=5\) og \(x_2=40\). Det ville give ratingen \[\hat{r}=2-0.02\cdot 5 + 0.05\cdot 40 = 3.9 \] Vi ser, at de prædikterede ratings ikke nødvendigvis giver et af tallene fra 1 til 5. Vi kan sågar risikere at ryge helt uden for intervallet fra 1 til 5, hvis filmen har meget ekstreme features. En film med \(100\%\) action og \(0\%\) romantik ville få ratingen \[\hat{r}=2-0.02\cdot 0 + 0.05\cdot 100 = 7 \] Det gør dog ikke noget. Vi vil aldrig kunne forudsige brugerens ratings præcist, men vi vil gerne have, at modellen kommer tæt på.
Vi ser nu på fortolkningen af vægtene i modellen (4). Hvis der hverken er kærlighed eller action i filmen, det vil sige hvis \(x_1=x_2=0\), så er \[\hat{r}= b + p_1\cdot 0 + p_2\cdot 0 = b\] Vi kan altså fortolke \(b\) som brugerens forventede rating af en film, der hverken indeholder kærlighed eller action. Dette minder om skæringen i en lineær regressionsmodel, og vi vil derfor omtale \(b\) som skæringen.
Vi ser også, at hvis andelen af kærlighedsscener \(x_1\) stiger med 1 procentpoint til \(x_1+1\), og \(x_2\) fastholdes, så stiger den prædikterede rating fra \[\hat{r}= b+p_1x_1 + p_2x_2\] til \[\hat{r}=b+p_1(x_1+1) + p_2x_2 = b+p_1x_1 + p_2x_2 +p_1\] Vi ser, at når \(x_1\) vokser med 1 enhed, så vokser ratingen med \(p_1\) (hvis altså \(x_2\) samtidig fastholdes). Dette minder om fortolkningen af hældningskoefficienten i en lineær regressionsmodel. Man kan derfor tænke på \(p_1\) som hældningen for \(x_1\). På samme vis kan man argumentere for, at hvis \(x_1\) fastholdes, mens \(x_2\) vokser med 1 enhed, så stiger ratingen med \(p_2\). Vi kan altså opfatte \(p_2\) som en hældningskoefficient for \(x_2\).
Fortegnet for \(p_2\) afslører, om brugeren vurderer action positivt eller negativt. Hvis \(p_2\) er positiv, stiger ratingen, jo mere action der er i filmen. Jo større \(p_2\) er, desto mere begejsret er brugeren for action. Hvis \(p_2\) er negativ, falder ratingen, jo mere action der er i filmen. Tilsvarende fortæller \(p_1\) noget om, hvor glad brugeren er for kærlighedsfilm. Vi kan derfor fortolke \(p_1\) og \(p_2\) som mål for brugerens præferencer. I eksempel 3 var \(p_1\) negativ, mens \(p_2\) var positiv, svarende til at brugeren godt kan lide action, men ikke kan lide romantik. Vi så da også, at actionfilmen fik højere rating end den romantiske film.
Modellen i (4) har mange ligheder med den lineære regressionsmodel, blot er der to variable \(x_1\) og \(x_2\) i stedet for en enkelt \(x\)-variabel. Den kaldes derfor for den multiple lineære regressionsmodel. Der indgår tre vægte, nemlig \(b\), \(p_1\) og \(p_2\). Disse vægte afhænger af brugerens præferencer og er derfor specifikke for den enkelte bruger. Der skal således laves en multipel lineær regressionsmodel for hver enkelt bruger.
Når vi har lavet en multipel lineær regressionsmodel for en bruger, kan vi bruge den til at prædiktere ratings. For hver film kan vi indsætte dens features i modellen og beregne brugerens forventede rating af filmen. Algoritmen kan så anbefale den film, som brugeren forventes at rate bedst.
Flere variable
Mere generelt kunne man vælge at betragte \(M\) features. Vi ville så have \(M\) variable \(x_1,\ldots, x_M\). For hver bruger ville vi have så have \(M\) vægte \(p_1,\ldots,p_M\), der beskriver brugerens præferencer, og en skæring \(b\). Vi prædiktere brugerens rating af en film som \[\hat{r} = b+ p_{1}x_{1} + p_{2}x_{2} + \dotsm + p_{M}x_{M} \tag{5}\] Dette kaldes en multipel lineær regressionsmodel med \(M\) variable.
Estimation af vægte
Vi vil altså gerne have lavet en multipel lineær regressionsmodel for en bruger. I det følgende ser vi bare på en model med to features som i (4). Men hvor får vi brugerens præferencevægte \(b,p_{1},p_{2}\) fra? Svaret er, at det vil vi få en computer til at lære ud fra data, som streamingtjenesten har indsamlet om brugerens tildligere ratings af film.6 Et eksempel på sådan et datasæt kan ses i tabel 3. Bemærk, at datasættet kun indeholder de film, som brugeren faktisk har set og tildelt en rating.
6 At lære en computer at lave prædiktioner ud fra et datasæt kaldes maskinlæring, eller på engelsk machine learning, og er et centralt element i de fleste former for kunstig intelligens.
| \(x_1\) | \(x_2\) | Rating | |
|---|---|---|---|
| Film 1 | 0 | 40 | 4 |
| Film 2 | 10 | 50 | 5 |
| Film 3 | 10 | 10 | 1 |
| Film 4 | 30 | 0 | 1 |
Vi betegner ratingen af \(j\)te film med \(r_j\) og dens to features med \(x_{1j}\) og \(x_{2j}\). Vores model prædikterer så brugerens rating af den \(j\)te film ved
\[ \hat{r}_{j} = b+p_{1}x_{1j} + p_{2}x_{2j} \tag{7}\]
Hvis modellen er god, skulle den prædikterede rating \(\hat{r}_j\) gerne ligge tæt på den faktiske rating \(r_j\). Vi vil derfor gerne have, at prædiktionsfejlen \(r_{j}-\hat{r}_{j}\) er tæt på 0. Da både positive og negative værdier langt fra \(0\) er problematiske, vælger vi at kvadrere, så vi slipper af med fortegnene. Vi vil så gerne have, at den kvadrerede prædiktionsfejl \((r_{j}-\hat{r}_{j})^2\) er så lav som muligt. Det skal gælde for hver eneste film i vores datasæt. Vi kræver derfor, at summen af alle de kvadrerede prædiktionsfejl for alle filmene skal være lav. Denne sum er givet ved \[E= (r_{1}-\hat{r}_{1})^2 + (r_{2}-\hat{r}_{2})^2 + \dotsm + (r_N-\hat{r}_N)^2 \] Her er \(N\) antallet af film, som brugeren har ratet.
Størrelsen \(E\) kaldes en tabsfunktion. Hvis modellen er god, skal tabsfunktionen altså være så lille som muligt. Tabsfunktionen afhænger af, hvordan vi har valgt vægtene \(b\), \(p_1\) og \(p_2\). Man kan altså betragte \(E\) som en funktion af vægtene. Vi ønsker at finde de vægte, der minimerer tabsfunktionen, svarende til at vores prædikterede ratings kommer så tæt på de faktiske ratings som muligt.7
7 Hvis du har hørt om mindste kvadraters metode i forbindelse med lineær regression, så er det samme princip, der bruges her.
8 Hvis du ikke kender til partielle afledede, eller du har brug for en genopfriskning, kan du læse om det i noten om Funktioner af flere variable.
Hvordan finder man minimum for en funktion, der afhænger af flere variable? Hvis der kun er én variabel, ved du, at man kan differentiere funktionen og lede efter minimum i de punkter, hvor den afledede funktion er nul. Noget tilsvarende gør sig gældende, når der er flere variable. Her er det bare de partielle afledede8, der alle skal være nul i et minimumspunkt. I vores tilfælde søger vi altså værdier af \(b\), \(p_1\) og \(p_2\), så \[ \begin{aligned} \frac{\partial E}{\partial p_1} = 0\\ \\ \frac{\partial E}{\partial p_2} = 0\\ \\ \frac{\partial E}{\partial b} = 0 \end{aligned} \] I opgaven nedenfor bliver du bedt om at beregne de partielle afledede af \(E\). Det fører til \[ \begin{aligned} &\frac{\partial E}{\partial p_1} = -2x_{11}(r_1-\hat{r}_1)- \dotsm -2x_{1N}(r_N-\hat{r}_N)\\ \\ &\frac{\partial E}{\partial p_2} = -2x_{21}(r_1-\hat{r}_1) - \dotsm -2x_{2N}(r_N-\hat{r}_N) \\ \\ &\frac{\partial E}{\partial b} = - 2(r_1-\hat{r}_1) - \dotsm - 2(r_N-\hat{r}_N) \end{aligned} \tag{8}\] For at finde minimumspunktet, skal vi altså løse ligningerne \[ \begin{aligned} &\frac{\partial E}{\partial p_1} = -2x_{11}(r_1-\hat{r}_1)- \dotsm -2x_{1N}(r_N-\hat{r}_N)=0\\ &\frac{\partial E}{\partial p_2} = -2x_{21}(r_1-\hat{r}_1) - \dotsm -2x_{2N}(r_N-\hat{r}_N)=0 \\ &\frac{\partial E}{\partial b} = - 2(r_1-\hat{r}_1) - \dotsm - 2(r_N-\hat{r}_N)=0 \end{aligned} \] Det viser sig, at disse ligninger kan løses eksplicit og give en formel for estimaterne for \(b\), \(p_1\) og \(p_2\). Det vil vi dog ikke gøre her.
Mere fleksible modeller
Multiple lineære regressionsmodeller er meget populære. En af grundene er, at de er simple og nemme at fortolke. Det kan være godt for Netflix med en model, der er nem at fortolke, hvis de for eksempel gerne vil lave markedsanalyser for at finde ud af, hvilke film, der hitter blandt brugerne. Men for at lave anbefalinger af film, har vi egentlig ikke brug for at forstå, hvor anbefalingen kommer fra, bare den virker. Der er altså ikke noget i vejen for at bruge en mere kompliceret model.
I mange sammenhænge tilpasser multiple lineære regressionsmodeller virkeligheden godt, men nogle gange er virkeligheden ikke lineær. For eksempel er der sikkert mange, der vil mene, at lidt action gør filmen mere spændende, men at der også skal være anden handling, for at filmen er interessant. De vil således give bedst ratings til film med et moderat indhold af action. En funktion med en \(\cap\)-formet graf ville give en bedre model. Dette er illustreret i figur 1.
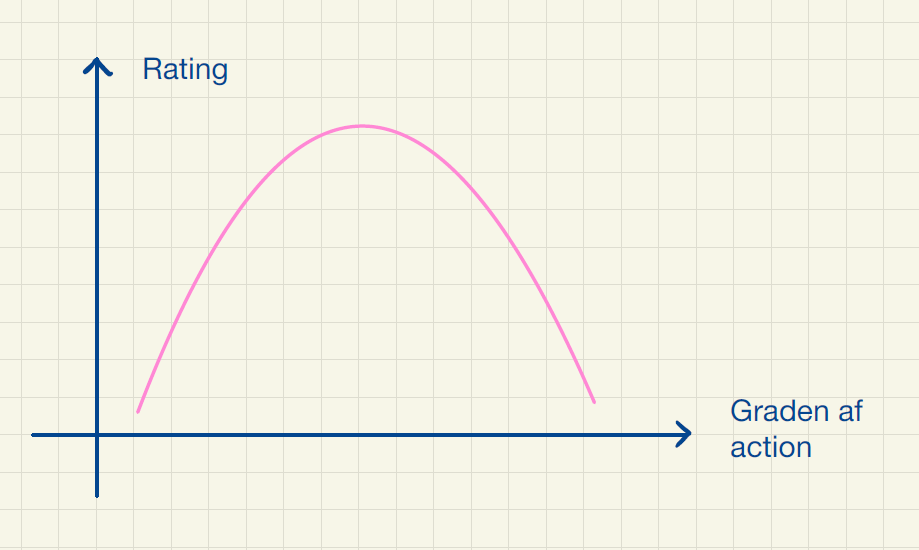
En mulighed kunne være at bruge et andengradspolynomium. Du kan læse mere om polynomiel regression i noten om Krydsvalidering.
Et andet problem opstår, hvis en film har meget ekstreme features. Så ryger dens prædikterede ratings nemt uden for intervallet 1 til 5. En funktion, hvis graf flader ud for meget store eller små featureværdier, ville være mere passende i dette tilfælde. Dette er illustreret i figur 2.
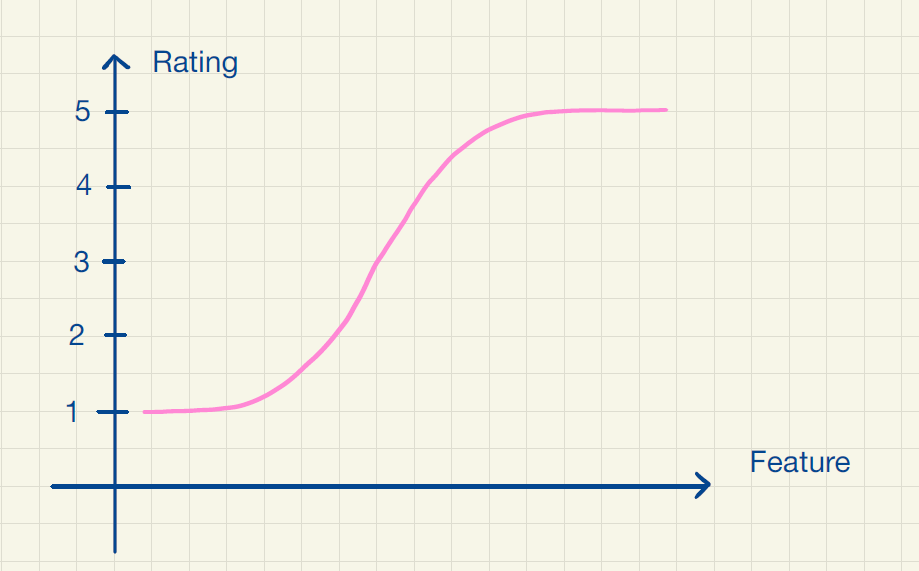
En af de vigtigste algoritmer inden for kunstig intelligens er de såkaldte neurale netværk. Neurale netværk giver mulighed for at prædiktere ratings som en ikke-lineær funktion af filmens features. De kan modellere en stor klasse af forskellige funktioner. Prisen for det er dog, at vi ikke får et pænt funktionsudtryk, som er nemt at fortolke. Men som nævnt er det heller ikke nødvendigt for at lave gode anbefalinger. En større udfordring ved neurale netværk er, at de kræver store mængder data. Det vil sige, at brugeren er nødt til at rate mange film, for at de kan benyttes. Du kan læse meget mere i vores forskellige noter om neurale netværk.
Endelig er der problemet med valg af features. Der er i princippet mange forskellige features, der kunne have betydning for brugernes ratings. Hvordan vælger man, hvilke der er mest relevante? Man kan selvfølgelig prøve sig frem, men så ryger man hurtigt ud i problemer med overfitting. Det kan du læse mere om i noten om Overfitting, modeludvælgelse og krydsvalidering. I næste afsnit skal vi se et eksempel på, hvordan man kan lade algoritmen vælge features selv.
Samarbejdsbaserede modeller for ratings
Da vi lavede den multiple lineære regressionsmodel, kiggede vi udelukkende på data for en enkelt bruger. Det viser sig dog, at man kan få meget mere information ud af også at lære af, hvordan andre brugere har ratet filmene. Derfor tager vi nu en samarbejdsbaseret tilgang, hvor vi tager udgangspunkt i et datasæt over alle brugeres ratings. Det kunne se ud som vist i tabel 4. NA står for "not available" og betyder, at brugeren ikke har set filmen.
| Film 1 | Film 2 | Film 3 | |
|---|---|---|---|
| Bruger 1 | 1 | NA | 4 |
| Bruger 2 | 2 | NA | 5 |
| Bruger 3 | 3 | 3 | 1 |
| Bruger 4 | NA | NA | 1 |
Matrixfaktorisering
Den algoritme, vi vil se på, kaldes matrixfaktorisering9. Algoritmen blev forslået i 2006 i forbindelse med konkurrencen "The Netflix Prize", hvor Netflix udlovede en præmie til den, der kunne forbedre firmaets egen algoritme til prædiktion af ratings med 10%. Matrixfaktorisering blev hurtigt et populært værktøj i konkurrencen og er stadig et vigtigt element i mange anbefalingssystemer.
9 Hvorfor den hedder det, bliver forklaret i en boks længere nede på siden, men det er ikke nødvendigt at kende til matricer, for at forstå hvordan algoritmen virker.
I den multiple lineære regressionsmodel valgte vi selv nogle features ved filmene. Det er dog ikke oplagt, hvilke features der er mest relevante. Man kan selvfølgelig prøve sig frem, men der kan hurtigt blive mange muligheder. Det kan også være svært at definere relevante features manuelt. Hvordan måler man for eksempel hvor sjov/alvorlig en film er? Det vi vil gøre her, er, at lade algoritmen selv vælge de \(M\) features. Vi betragter altså \(x_1,\ldots,x_M\) som ukendte underliggende variable, også kaldet latente variable, som har indflydelse på, hvordan man vurderer filmen. Man kunne forestille sig, at de måler diffust definerede egenskaber ved filmen, så som "hvor sjov filmen er" eller "hvor gode skuespillerne er". Men vi det ikke, og vi behøver heller ikke at vide det, bare der kommer gode anbefalinger ud af det!
Vi kalder \(i\)te brugers rating af \(j\)te film for \(r_{ij}\). Vi vil nu gerne lave en algoritme, der kan prædiktere \(i\)te brugers rating af \(j\)te film. Det er altså den værdi, der står i \(i\)te række og \(j\)te søjle i tabel 4. Hver film har sine egne værdier af de \(M\) features. For \(j\)te film betegner vi dem \(x_{1j},\ldots,x_{Mj}\). Disse værdier kalder vi featurevægtene. Den \(i\)te brugers præferencer for de \(M\) features beskrives ved præferencevægtene \(p_{i1},\ldots,p_{iM}\). Vi modellerer så \(i\)te brugers rating af \(j\)te film ved \[\hat{r}_{ij} = p_{i1}x_{1j} + p_{i2}x_{2j} + \dotsm + p_{iM}x_{Mj} \tag{9}\] Det minder om den multiple lineære regressionsmodel (5). Forskellen er, at featurevægtene ikke er givet på forhånd, men er nogle, vi skal estimere ud fra data. Hvis datasættet indeholder \(p\) film, og hver af dem har \(M\) featurevægte, så vil der være \(M\cdot p\) featurevægte i alt. Hvis der er \(n\) brugere, og hver af dem har \(M\) præferencevægte, vil der samlet være \(n\cdot M\) præferencevægte. Det giver i alt \(M\cdot p + n\cdot M\) vægte, som skal bestemmes. I et typisk datasæt vil både \(n\) og \(p\) være store, så der vil være et stort samlet antal vægte. Hvis \(M\) vælges relativt lille, vil det samlede antal vægte dog være lille i forhold til det samlede antal kombinationer af film og bruger, som vil være \(n\cdot p\). I stedet for at skulle estimere samtlige \(n\cdot p\) værdier af \(r_{ij}\), skal vi kun estimere \(M\cdot p + n\cdot M\) vægte.
Skæring i modellen
Da vi lavede multipel lineær regression, var der også en skæring i modellen, som svarede til ratingen, når alle features var nul. Tilsvarende er det oplagt at tilføje en skæring i
(9). Det gøres ofte med modellen \[\hat{r}_{ij} = b + c_i + d_j+ p_{i1}x_{1j} +p_{i2}x_{2j} + \dotsm + p_{iM}x_{Mj} \] Her angiver \(b\) den gennemsnitlige rating for alle film, når alle featurevægte er nul. Hver bruger har desuden et personligt led \(c_i\), der tager højde for, at nogle brugere er mere tilbøjelige til at give høje ratings end andre. Hvis \(c_i\) er positiv, giver brugeren højere ratings end gennemsnittet, mens hvis \(c_i\) er negativ, giver brugeren lavere ratings end gennemsnittet. På samme måde har hver film et led \(d_j\), der korrigerer for, at nogle film generelt får højere ratings end andre. Hvis \(d_j\) er positiv, får filmen højere ratings end gennemsnittet, mens hvis \(d_j\) er negativ, får filmen dårligere ratings end gennemsnittet. For nemheds skyld arbejder vi videre med modellen (9) i det følgende.
Estimation af vægte
For at kunne bruge modellen i (10) skal vi have estimeret alle featurevægtene \(x_{1j},x_{2j},\ldots,x_{Mj}\) og alle præferencevægtene \(p_{i1},p_{i2},\ldots, p_{iM}\). Til det formål tager vi udgangspunkt i et datasæt på formen i tabel 4, som streamingtjenesten har indsamlet.
Vi ønsker at prædiktere \(i\)te brugers rating af \(j\)te film ved \[\hat{r}_{ij} = p_{i1}x_{1j} + p_{i2}x_{2j} + \dotsm + p_{iM}x_{Mj} \tag{10}\] Som i den multiple lineære regressionsmodel, sammenligner vi prædiktionen \(\hat{r}_{ij}\) med de faktiske ratings \(r_{ij}\). Hvis modellen er god, vil vi gerne have, at prædiktionsfejlen \(r_{ij}-\hat{r}_{ij}\) er tæt på 0 svarende til, at den kvadrerede prædiktionsfejl \((r_{ij}-\hat{r}_{ij})^2\) er lille. Vi definerer en tabsfunktion \[E=\sum_{r_{ij} \neq NA} (r_{ij}-\hat{r}_{ij})^2 \] Her betyder \(r_{ij}\neq NA\) under sumtegnet, at vi kun skal tage summen af de led, hvor vi kender den faktiske rating (\(r_{ij}=NA\) betød jo, at brugeren ikke havde ratet filmen, så i det tilfælde kan vi ikke udregne en prædiktionsfejl).
Igen ønsker vi at finde de vægte, der minimerer tabsfunktionen. I modsætning til multipel lineær regression, kan de ligninger, man får ud af at udregne de partielle afledede og sætte dem lig nul, ikke løses eksplicit. I stedet kan man finde minimum ved hjælp af en populær algoritme inden for kunstig intelligens, der hedder gradientnedstigning. For at kunne bruge den, skal man kende de partielle afledede af \(E\) med hensyn til vægtene. For at finde dem, kan vi først bemærke, at \(E\) er en sum, og en sum differentieres som bekendt ledvist. I en opgave nedenfor viser I, at de partielle afledede af et enkelt led i \(E\) er givet ved
\[ \begin{aligned} \frac{\partial }{\partial p_{im}} (r_{ij}-\hat{r}_{ij})^2 = -2 (r_{ij}-\hat{r}_{ij})x_{mj}\\ \frac{\partial }{\partial x_{mj}} (r_{ij}-\hat{r}_{ij})^2 = -2 (r_{ij}-\hat{r}_{ij})p_{im} \end{aligned} \tag{11}\] Desuden gælder der for \(l\neq i\), at \[ \frac{\partial }{\partial p_{lm}} (r_{ij}-\hat{r}_{ij})^2 = 0 \tag{12}\] og for \(k \neq j\) \[ \frac{\partial }{\partial x_{mk}} (r_{ij}-\hat{r}_{ij})^2 = 0 \tag{13}\]
Disse formler gør, at en computer nemt kan lave gradientnedstigning.
Moderne anbefalingssystemer
Vi har skelnet mellem indholdsbaserede og samarbejdsbaserede anbefalingssystemer. De algoritmer der bruges i praksis indeholder dog elementer fra begge dele. Du vil også se, at tjenesterne laver forskellige slags anbefalinger, for eksempel af typen "specielt til dig", "andre har også set" eller "fordi du så".
Nogle af de datatyper, tjenesterne indsamler, er særligt komplicerede. Det kunne for eksempel være rækkefølgen, du ser filmene i. De senest sete film er typisk mest relevante for dit næste valg. Hvis du lige har set fem kattevideoer på YouTube, er det sandsynligt, at du er i humør til endnu en kattevideo. Her benyttes faktisk nogle af de samme algoritmer, som bruges af de store sprogmodeller, der indgår i blandt andet ChatGPT og Google Translate (du kan læse mere i vores noter om sprogmodeller). Ligesom filmenes rækkefølge er vigtig, er det nemlig også vigtigt for sprogmodellerne at kunne tage højde for ordenes rækkefølge i en tekst. Modellerne har derfor meget tilfælles.
Som nævnt er det afgørende i konkurrencen mellem streamingtjenester, at de er i stand til at levere gode anbefalinger til brugerne. Derfor arbejdes der også til stadighed på at gøre algoritmerne bedre.