Argument for at de retningsafledede kan udregnes med et prikprodukt ved hjælp af middelværdisætningen

Vi vil her argumentere for formlen for, at de retningsafledede kan udregnes som et prikprodukt:

$$D_{\overrightarrow{u}}f(x_0,y_0)=\mathrm{\nabla }f(x_0,y_0)\cdot \overrightarrow{u}$$

ved at bruge middelværdisætningen for funktioner af én variabel:

Sætning 1 (Middelværdisætningen) Hvis $f$ er kontinuert på $[a;b]$ og differentiabel i $]a;b[$, så findes der et tal $c$ mellem $a$ og $b$, så tangenthældningen i $c$ er lig med middelværdien af hældningen på hele intervallet $[a;b]$. Det vil sige, at $$f^{{}^{\prime }}\left(c\right)=\frac{f\left(b\right)-f(a)}{b-a}$$

Resultatet i middelværdisætningen kan omskrives til

$$\begin{array}{}\text{(1)}& f\left(b\right)-f\left(a\right)=f^{{}^{\prime }}\left(c\right)\cdot (b-a)\end{array}$$

som er det, vi får brug for. Middelværdisætningen virker indlysende korrekt, hvis man prøver at tegne situationen, og beviset for middelværdisætningen kan findes i flere gymnasiebøger.

Inden vi går til argumentet for formlen for de retningsafledede, vil vi se på et enkelt eksempel med middelværdisætningen.

Eksempel 1 Funktionen $f\left(x\right)=\sqrt{x}$ er kontinuert på $[0;4]$ og differentiabel i $]0;4[$, så betingelserne for at bruge middelværdisætningen er opfyldt.

Der findes så et tal $c$ mellem 0 og 4, så $f^{{}^{\prime }}\left(c\right)=\frac{f\left(4\right)-f(0)}{4-0}$.

Vi ved, at $f^{{}^{\prime }}\left(x\right)=\frac{1}{2\sqrt{x}}$ så ligningen ovenfor bliver $$\frac{1}{2\sqrt{c}}=\frac{\sqrt{4}-\sqrt{0}}{4-0}$$ Det vil sige, at $$\frac{1}{2\sqrt{c}}=\frac{1}{2}$$ hvilket giver $c=1$.

Tangenthældningen af grafen for $f\left(x\right)=\sqrt{x}$ i $c=1$ er altså det samme som middelværdien af hældningen af grafen på hele intervallet $[a;b]=[0;4]$, det vil sige hældningen af den sekant, der forbinder startpunktet $(0,f\left(0\right))$ og slutpunktet $(4,f\left(4\right))$.

På figur 1 illustreres dette princip.

Figur 1: Illustration af middelværdisætningen. Her har tangenten i $(1,f(1))$ (den grønne linje) samme hældning som sekanten gennem $(0,f(0))$ og $(4,f(4))$ (den blå linje).

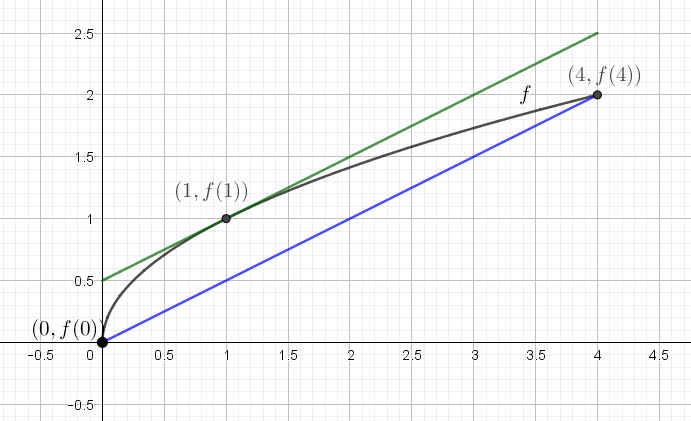
Middelværdisætningen siger altså bare, at hvis man forbinder start og slutpunktet – den blå linje – og udregner dens hældning, så kan man altid finde mindst et punkt i det indre af intervallet, hvor tangenten i punktet – den grønne linje – har samme hældning. I eksemplet fandt vi et bestemt $c$, som vi ifølge middelværdisætningen vidste, at vi kunne. Når vi i det følgende skal tænke endnu mere generelt, så bliver middelværdisætningen nyttig.

Vi vender nu tilbage til definitionen af de retningsafledede. Vi får i det følgende brug for at antage, at både $f_x(x,y)$ og $f_y(x,y)$ eksisterer, så vi kan bruge middelværdisætningen. Desuden får vi også brug for at antage, at $f_x(x,y)$ og $f_y(x,y)$ er kontinuerte på en omegn af $(x_0,y_0)$.

Vi husker på, at de retningsafledede var defineret ved

$$\begin{array}{}\text{(2)}& D_{\overrightarrow{u}}f(x_0,y_0)=\underset{h\to 0}{lim}\frac{f(x_0+h{u}_1,y_0+h{u}_2)-f(x_0,y_0)}{h}\end{array}$$

Vi omskriver nu tælleren i (2) for at kunne bringe middelværdisætningen i spil $$\begin{array}{rl}f(x_0+h\cdot u_1,y_0+h& \cdot u_2)-f(x_0,y_0)=\\ & f(x_0+h\cdot u_1,y_0+h\cdot u_2)\\ & -f(x_0,y_0+h\cdot u_2)+f(x_0,y_0+h\cdot u_2)\\ & -f(x_0,y_0)\end{array}$$ Bemærk, at vi har lagt et led til og trukket det samme led fra (markeret med rødt). Det svarer til, at vi har indskudt et punkt i $xy$-planen, som illustreret i figur 2.

Figur 2: Et rødt punkt er indskud i $xy$-planen.

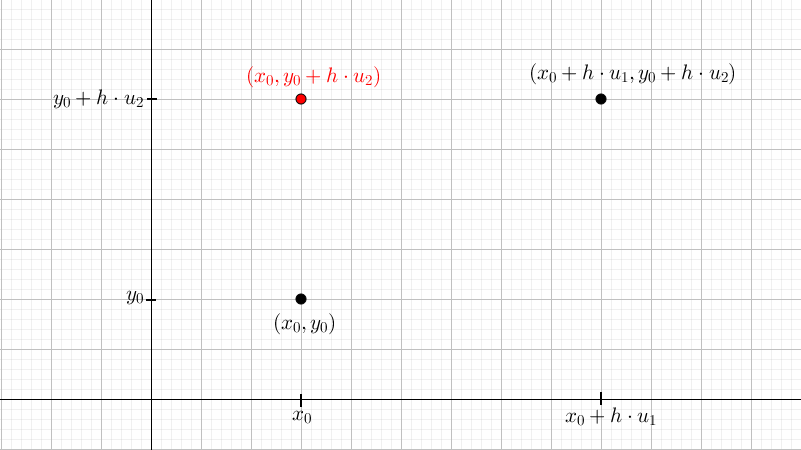
Vi ser nu, at de to første led kun afviger på $x$-koordinaten (markeret med blåt nedenfor), og de to sidste led afviger kun på $y$-koordinaten (markeret med grønt): $$\begin{array}{}\text{(3)}& \begin{array}{rl}f(x_0+h\cdot u_1,y_0+h\cdot u_2)-f(x_0,y_0)& =\\ f(x_0+h\cdot u_1,y_0+h\cdot u_2)-& f(x_0,y_0+h\cdot u_2)+\\ f(x_0,y_0+h\cdot u_2)-& f(x_0,y_0)\end{array}\end{array}$$

Afvigelsen på henholdsvis $x$- og $y$-koordinaten er vist i figur 3.

Figur 3: Afvigelsen på $x$-koordinaten er markeret med blåt, mens afvigelsen på $y$-koordinaten er markeret med grønt.

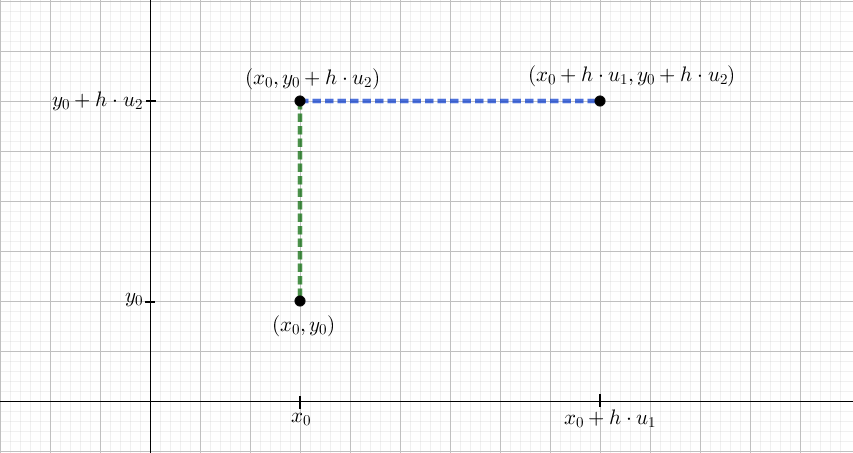
Ved at bruge den omskrevne middelværdisætning i (1) på de to snitfunktioner $f(x,y_0+h\cdot u_2)$ som en funktion af $x$ og $f(x_0,y)$ som en funktion af $y$, får vi nu følgende:

$$\begin{array}{r}f(x_0+h\cdot u_1,y_0+h\cdot u_2)-f(x_0,y_0+h\cdot u_2)=f_x(c_1,y_0+h\cdot u_2)\cdot h\cdot u_1\end{array}$$ og $$f(x_0,y_0+h\cdot u_2)-f(x_0,y_0)=f_y(x_0,c_2)\cdot h\cdot u_2$$

Her har vi brugt, at den afledede af en snitfunktion, hvor vi kun varierer $x$ er $f_x$, og den afledede af en snitfunktion, hvor vi kun varierer $y$ er $f_y$. Tallet $c_1$ ligger mellem $x_0$ og $x_0+h\cdot u_1$, og tallet $c_2$ ligger mellem $y_0$ og $y_0+h\cdot u_2$. Dette er vist i figur 4.

Figur 4: Tallet $c_1$ ligger mellem $x_0$ og $x_0+h\cdot u_1$, og tallet $c_2$ ligger mellem $y_0$ og $y_0+h\cdot u_2$.

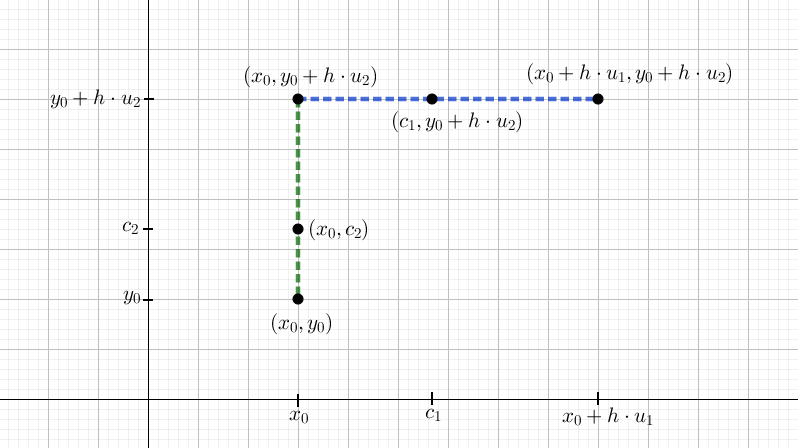
Indsætter vi de to udtryk ovenfor på højreside i (3) får vi $$\begin{array}{c}f(x_0+h\cdot u_1,y_0+h\cdot u_2)-f(x_0,y_0)=f_x(c_1,y_0+h\cdot u_2)\cdot h\cdot u_1+\hfill \\ \hfill f_y(x_0,c_2)\cdot h\cdot u_2\end{array}$$

Og bruges dette i definitionen for den retningsafledede i (2) ender vi med $$\begin{array}{rl}{D}_{\overrightarrow{u}}f(x_0,y_0)& =\underset{h\to 0}{lim}\frac{f(x_0+h\cdot u_1,y_0+h\cdot u_2)-f(x_0,y_0)}{h}\\ & =\underset{h\to 0}{lim}\frac{f_x(c_1,y_0+h\cdot u_2)\cdot h\cdot u_1+f_y(x_0,c_2)\cdot h\cdot u_2}{h}\end{array}$$ Vi kan nu dividere $h$ op i hvert led og får $$\begin{array}{}\text{(4)}& \begin{array}{rl}{D}_{\overrightarrow{u}}f(x_0,y_0)& =\underset{h\to 0}{\text{lim}}{f}_x(c_1,y_0+h\cdot u_2)\cdot u_1+f_y(x_0,c_2)\cdot u_2\\ & =\underset{h\to 0}{lim}\left(\begin{array}{c}{f}_x(c_1,y_0+h\cdot u_2)\\ f_y(x_0,c_2)\end{array}\right)\cdot \left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)\end{array}\end{array}$$ hvis grænsen eksisterer.

Husk på, at $c_1$ ligger i intervallet $(x_0,x_0+h\cdot u_1)$ og $c_2$ ligger i intervallet $(y_0,y_0+h\cdot u_2)$. Derfor vil

$$\underset{h\to 0}{lim}(c_1,y_0+h\cdot u_2)=(x_0,y_0)$$ og $$\underset{h\to 0}{lim}(x_0,c_2)=(x_0,y_0)$$

Vi startede med at antage, at de partielle afledede er kontinuerte. Det får vi brug for nu. Det betyder nemlig, at grænseværdien i (4) eksisterer, og vi får det ønskede resultat

$$D_{\overrightarrow{u}}f(x_0,y_0)=\left(\begin{array}{c}{f}_x(x_0,y_0)\\ f_y(x_0,y_0)\end{array}\right)\cdot \left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)=\mathrm{\nabla }f(x_0,y_0)\cdot \overrightarrow{u}$$ Det var netop, hvad vi ønskede at vise¹.

¹ Vi startede med at antage, at de partielle afledede eksisterer og er kontinuerte på en omegn. Bemærk, at vi ud fra den antagelse nu har vist, at alle de retningsafledede også vil eksistere.