Clustering med K-means
K-means
Når \(K\)-means metoden bruges, er målet at inddele nogle observationer i grupper, så observationerne i hver gruppe minder meget om hinanden.
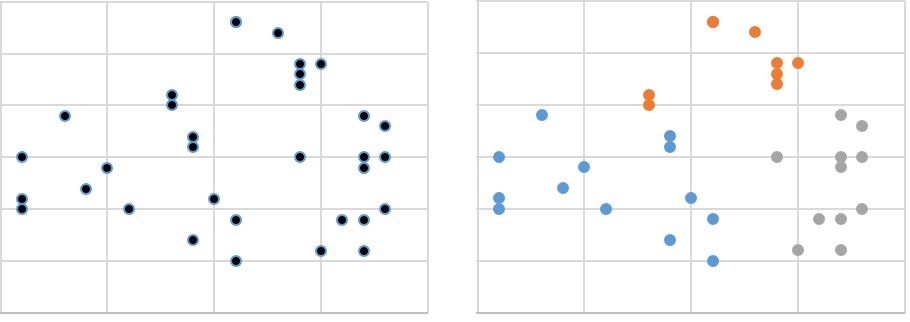
På figur 1 til venstre ses en række punkter, hvor vi ønsker at inddele punkterne i 3 grupper. Man kan nok godt få en idé om, hvordan grupperne kan laves alene ved at se på billedet til venstre. På figur 1 til højre ses et bud på en løsning, som ser fornuftig ud, men ved nogle punkter tænker man nok alligevel lidt, om de nu skulle have været i den orange eller blå gruppe. Når vi arbejder med \(K\)-means, så er idéen, at vi ikke på forhånd har nogle observationer, hvor vi ved hvilken gruppe, de tilhører. Med andre ord har vi altså ikke et træningsdatasæt at gå ud fra her. Derfor taler man også om unsupervised learning. Det eneste, vi ved om vores punkter i figur 1, er deres \(x\)- og \(y\)-koordinat og ud fra det, skal vi så prøve at danne nogle grupper. Antallet af grupper ved man faktisk heller ikke nødvendigvis noget om – så her er det et valg, at vi har besluttet at prøve at inddele data i 3 grupper. Det kunne i princippet lige så godt have været 2 eller 4 grupper eller noget helt andet!
Observationerne vil vi her kalde for \(\vec{x_1}, \vec{x_2},....,\vec{x_n}\), så der i alt er \(n\) observationer. Hver observation er et punkt med \(d\) koordinater (som dog behandles, som var det vektorer/stedvektorer), og som udgangspunkt benyttes euklidisk afstand til at bestemme afstand mellem punkter. I eksemplet i figur 1 er \(d=2\), fordi alle punkter i planen har 2 koordinater.
Givet et heltal \(k\), så ønsker vi at opdele de \(n\) observationer \(\vec{x_1}, \vec{x_2},....,\vec{x_n}\) i \(k\) grupper, som vi kalder for \(S_1,S_2,....,S_k\). Antallet af observationer i gruppen1 \(S_i\) betegnes med \(|S_i|\).
1 En gruppe \(S_i\) er egentlig en mængde, og \(|S_i|\) er kardinaliteten af denne mængde – altså antallet af elementer i mængden.
Hele idéen i \(K\)-means metoden er, at det skal være sådan, at observationerne i samme gruppe ligger tæt på hinanden. Det er også sådan, at vi har farvet punkterne til højre i figur 1.
Hvis man skal oversætte det til matematik, så betyder det, at vi ønsker at minimere følgende sum (som vi kalder for \(SUMPAR\))
\[SUMPAR=\sum_{i=1}^{k}\frac{1}{|S_i|}\sum_{\vec p\in S_i}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2\] Det ser måske lidt voldsomt ud, men lad os prøve at nedbryde ovenstående lidt. Vi forestiller os, at vi har de \(k\) grupper \(S_1, S_2, \dots , S_k\). Vi ser først på et punkt \(\vec p \in S_i\). Den kvadrerede afstand til et andet punkt \(\vec q\) i samme gruppe er givet ved udtrykket
\[ \|\vec p- \vec q\|^2 \]
Det vil sige, den euklidiske afstand mellem \(\vec p\) og \(\vec q\) opløftet i anden. Den gennemsnitlige kvadrerede afstand til alle punkter i samme gruppe \(S_i\) vil derfor være
\[\frac{1}{|S_i|} \sum_{\vec q \in S_i} \|\vec p- \vec q\|^2 \]
Det er altså den gennemsnitlige kvadrerede afstand fra ét punkt \(\vec p\) til alle andre punkter i samme gruppe – inklusiv punktet selv. Vi vil nu lægge alle disse gennemsnitlige kvadrerede afstande sammen for alle punkter i \(S_i\). Gør vi det, får vi:
\[ \sum_{\vec p\in S_i}\frac{1}{|S_i|}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2 \]
Da størrelsen \(\frac{1}{|S_i|}\) indgår i alle led i den yderste sum, kan vi sætte \(\frac{1}{|S_i|}\) uden for det yderste sumtegn2. Derfor kan vi omskrive ovenstående til
2 Det svarer bare til at sætte uden for en parentes.
\[ \frac{1}{|S_i|}\sum_{\vec p\in S_i}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2 \]
Det her vil vi gerne gøre for alle grupper, og derfor ender vi samlet set med
\[ SUMPAR=\sum_{i=1}^{k}\frac{1}{|S_i|}\sum_{\vec p\in S_i}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2 \tag{1}\]
Alt i alt får vi altså, at \(SUMPAR\) giver summen af hvert punkts gennemsnitlige kvadrerede afstand til alle punkter i samme gruppe som sig selv (inklusiv sig selv).
Idéen er så nu, at vi vil prøve at bestemme grupperne \(S_1, S_2, \dots, S_k\) sådan, at denne sum bliver så lille som muligt. Det vil nemlig svare til, at de punkter, der ligger tæt på hinanden, kommer i samme gruppe, og punkter, som ligger langt væk fra hinanden, kommer i forskellige grupper.
Det er desværre ikke lige til at finde den optimale løsning på dette problem, men her angives en metode/algoritme, som forhåbentlig finder en god løsning.
Algoritme
Vi vil nu se på en metode til at finde en god løsning til \(K\)-means problemet. Vi får her brug for "midterpunktet" for hver gruppe, som vi vil kalde for \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\). Ved midterpunktet vil vi simpelthen bare forstå gennemsnittet af alle punkter i den pågældende gruppe.
I algoritmen vil vi prøve at minimere følgende sum
\[ SUMMIDT=\sum_{i=1}^{k}\sum_{\vec p\in S_i}\|\vec p-\vec{\mu_i}\|^2 \tag{2}\]
Her summeres altså den kvadrerede afstand fra hvert punkt til midterpunktet for gruppen, som punktet er i. Og det gør man så for alle grupper og lægger alle de kvadredede afstande sammen. Senere vil vi se på sammenhængen mellem summen \(SUMPAR\) og summen \(SUMMIDT\).
Spørgsmålet er nu, hvordan man kommer igang med at fastlægge grupper og midterpunkter, for vi kender ikke mængderne \(S_1,S_2,....,S_k\) og dermed heller ikke midterpunkterne \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\).
For at løse det problem vil vi bruge følgende fremgangsmåde/algoritme:
Start med at tage hver eneste observation og tilføj den til en tilfældig gruppe (der skal mindst være én observation i hver gruppe).
Midterpunkterne bestemmes ved at lade
\[ \vec{\mu_i}=\frac{1}{|S_i|}\sum_{\vec p\in S_i}\vec p \]
For hver af de \(n\) observationer findes det midterpunkt, der har den mindste afstand til punktet. Hvis det for en observation \(\vec{x_i}\) er midterpunktet \(\vec{\mu_a}\), der er nærmest, skal \(\vec{x_i}\) være i mængden \(S_a\).
Gentag trin 2 og 3 indtil vi kommer til et tidspunkt, hvor ingen punkter kommer til at skifte til en anden gruppe.
Det virker jo meget rimeligt. Så er spørgsmålet bare, om denne fremgangsmåde virkelig fungerer! Det vil vi se nærmere på i afsnittet om sammenhængen mellem SUMPAR og SUMMIDT. Men lad os starte med at se på et par eksempler.
Eksempel på beregning af midterpunkter
Først kunne det måske være rart at få en fornemmelse af, hvorfor \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\) betegnes som midterpunkter.
Eksempel 1 Vi forestiller os, at vi har to grupper med følgende punkter:
Gruppe 1 med punkterne \((3,9)\) og \((7,11)\).
Gruppe 2 med punkterne \((10,30)\), \((17,34)\), \((12,27)\) og \((11,32)\).
Som nævnt tidligere kan vi tænke på hvert punkt som stedvektoren til punktet.3 Vi kan nu finde midterpunktet for den første gruppe:
3 Husk at et punkt og stedvektoren til punktet har samme koordinater.
\[\vec{\mu_1}=\frac{1}{|S_1|}\sum_{\vec p\in S_1}\vec p = \frac{\begin{pmatrix} 3 \\ 9\end{pmatrix} + \begin{pmatrix} 7 \\ 11\end{pmatrix}}{2}= \frac{\begin{pmatrix} 10 \\ 20\end{pmatrix} }{2} = \begin{pmatrix} 5 \\ 10\end{pmatrix}\]
Midterpunktet for den første gruppe har altså koordinatsæt \((5,10)\).
Midterpunktet for den anden gruppe bliver tilsvarende
\[\vec{\mu_2}=\frac{1}{|S_2|}\sum_{\vec p\in S_2}\vec p = \frac{\begin{pmatrix} 10 \\ 30\end{pmatrix} + \begin{pmatrix} 17 \\ 34\end{pmatrix} + \begin{pmatrix} 12 \\ 27\end{pmatrix} + \begin{pmatrix} 11 \\ 32\end{pmatrix}}{4}= \frac{\begin{pmatrix} 50 \\ 123 \end{pmatrix} }{4} = \begin{pmatrix} 12.5 \\ 30.75 \end{pmatrix}\]
Midterpunktet for den anden gruppe har så koordinatsæt \((12.5, 30.75)\).
Dette er illustreret i figur 2.
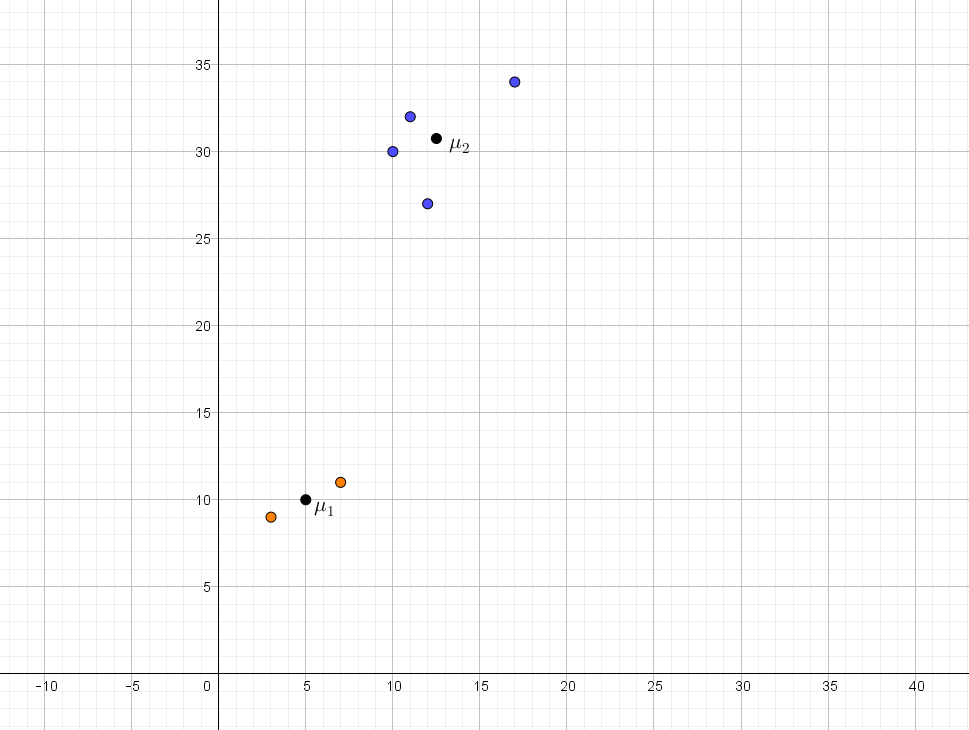
På figur 2 bliver det tydeligt, hvorfor det er fornuftigt at vælge midterpunkterne, som det sker i trin 2 i algoritmen – midterpunkterne ligger simpelthen i "midten" af hver gruppe.
Eksempel på algoritmen
Lad os nu prøve at bruge algoritmen på punkterne fra eksempel 1. I figur 3 ses punkterne indtegnet, men uden angivelse af hvilken gruppe hvert enkelt punkt tilhører.
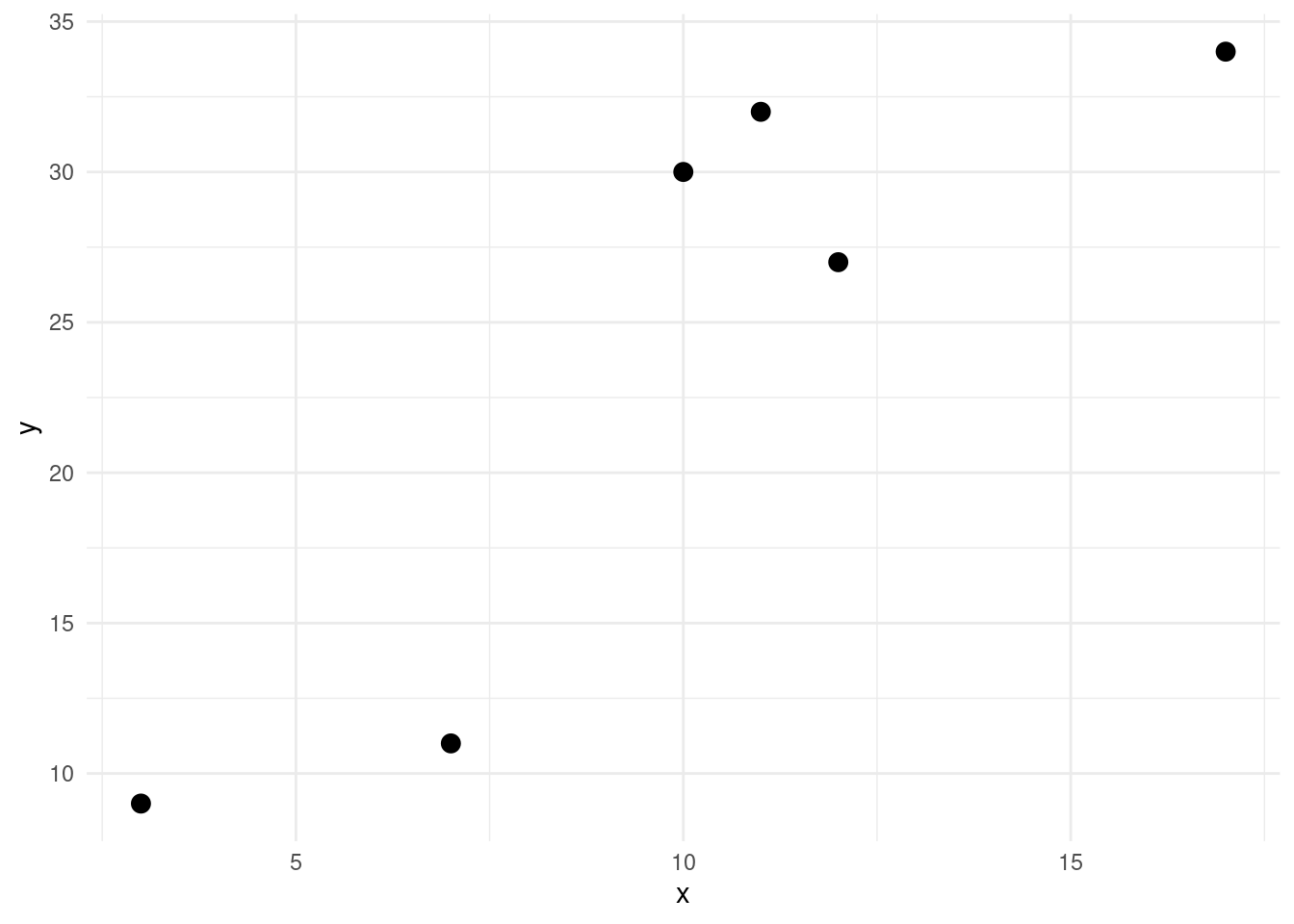
I trin 1 skal vi tilføje hver observation i en tilfældig gruppe. Et sådant valg ses i figur 4.
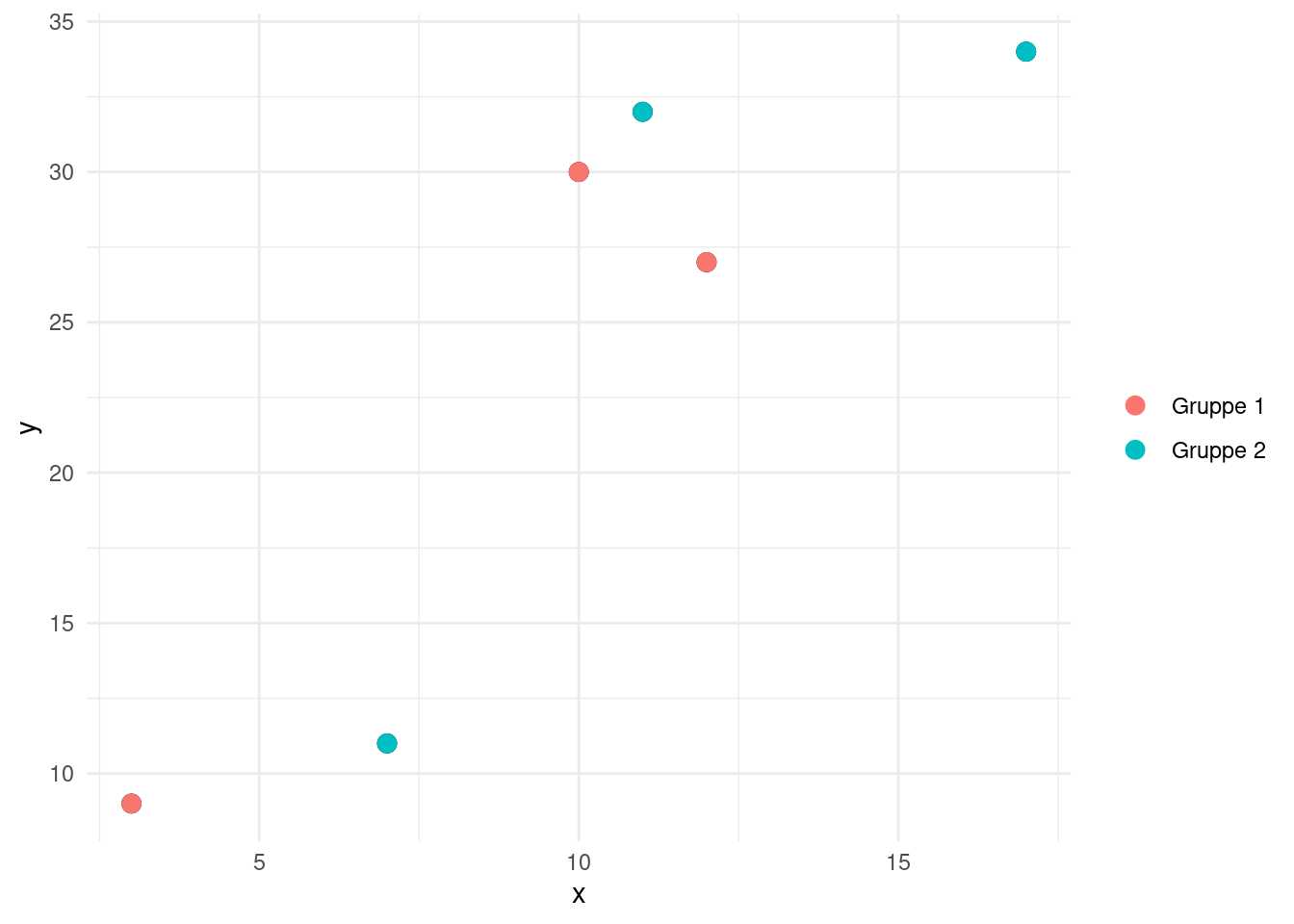
Vi skal nu have beregnet midtpunkterne i hver af de to grupper. Gør man det fås:
\[ \vec{\mu_1} = \begin{pmatrix} 8.33 \\ 22.0 \end{pmatrix} \quad \textrm{og} \quad \vec{\mu_2} = \begin{pmatrix} 11.7 \\ 25.7 \end{pmatrix} \] Disse to midtpunkter er indtegnet i figur 5 og markeret med et plus.
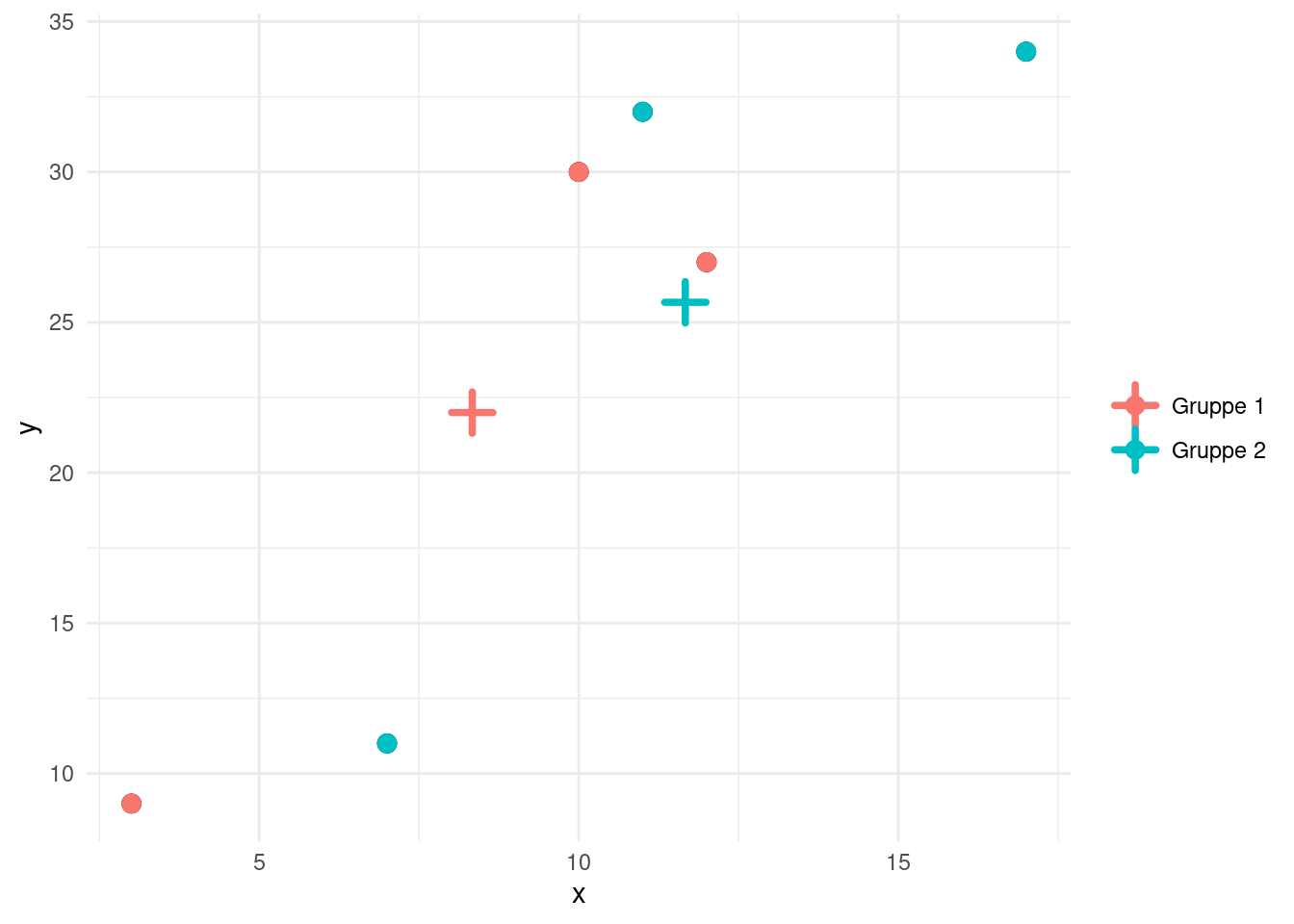
I trin 3 skal vi have beregnet afstand fra hver af de 6 punkter til hver af de to midtpunkter. For eksempel bliver afstanden \(d\) fra punktet \((3,9)\) til punktet med stedvektor \(\vec{\mu_1}\) være:
\[ d=\sqrt{(3-8.33)^2+(9-22.0)^2}=14.05 \] Resultatet af at beregne alle afstande på denne måde ses i tabel 1.
| Afstand til \(\vec{\mu_1}\) | Afstand til \(\vec{\mu_2}\) |
|---|---|
| 14.05 | 18.79 |
| 11.08 | 15.39 |
| 8.172 | 4.643 |
| 14.8 | 9.894 |
| 6.2 | 1.374 |
| 10.35 | 6.368 |
Vi skal nu afgøre hvilken gruppe, de enkelte punkter skal tilhøre, ved at se på hvilket midtpunkt som hvert enkelt punkt ligger tættest på. For eksempel kan vi i tabel 1 se, at det første punkt \((3,9)\) ligger tættest på \(\vec{\mu_1}\), og det punkt skal derfor (fortsat) hører til gruppe 1.
I tabel 2 ses den oprindelige gruppe samt den nye gruppe for hvert punkt.
| Afstand til \(\vec{\mu_1}\) | Afstand til \(\vec{\mu_2}\) | Opr. gruppe | Ny gruppe |
|---|---|---|---|
| 14.05 | 18.79 | 1 | 1 |
| 11.08 | 15.39 | 2 | 1 |
| 8.172 | 4.643 | 1 | 2 |
| 14.8 | 9.894 | 2 | 2 |
| 6.2 | 1.374 | 1 | 2 |
| 10.35 | 6.368 | 2 | 2 |
I figur 6 ses punkterne indtegnet med en angivelse af den nye inddeling (men stadig med de først beregnede midterpunkter).
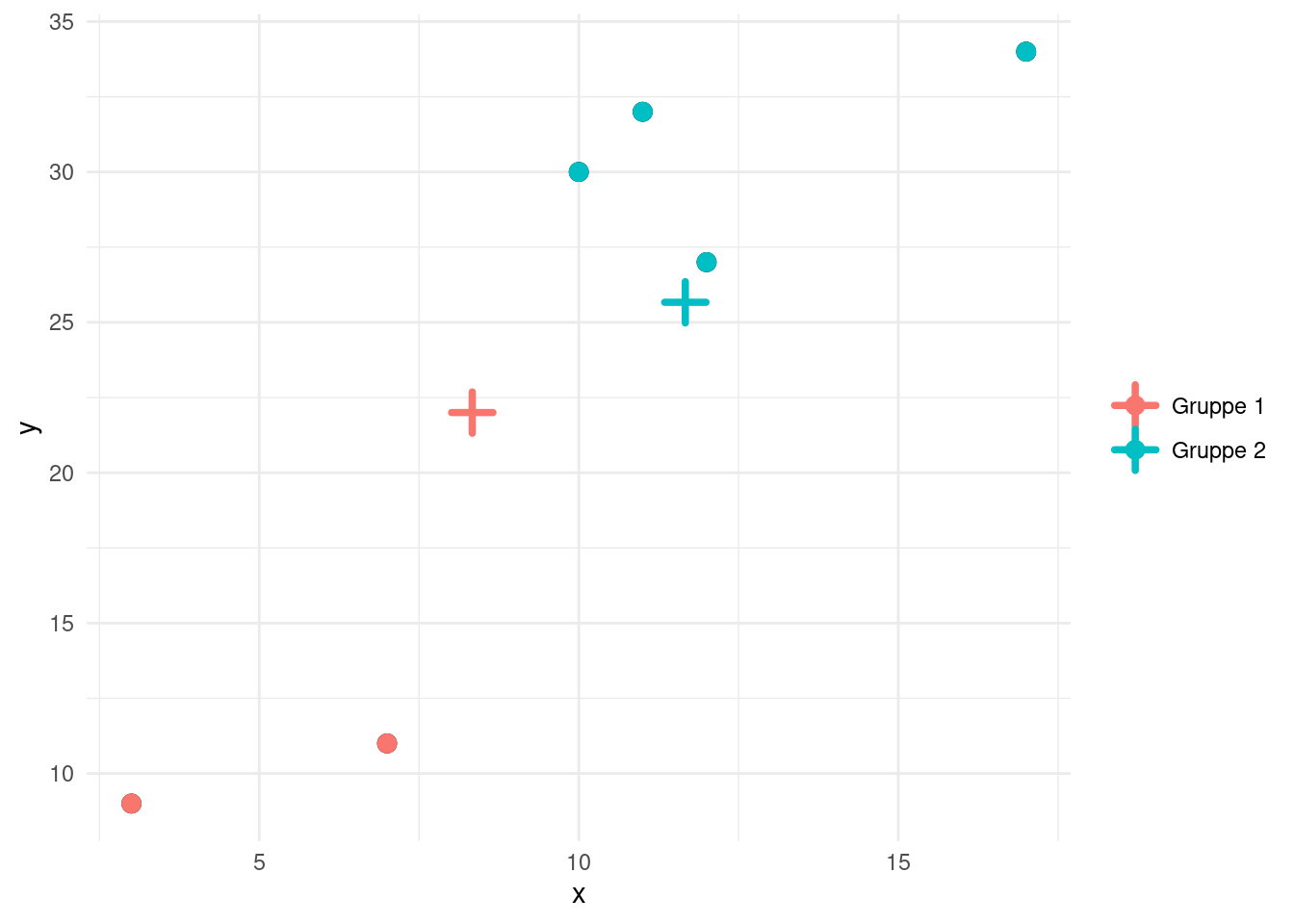
Vi skal nu i gang med det næste gennemløb af algoritmen, og vi bestemmer derfor først de nye midtpunkter. Gør man det fås:
\[ \vec{\mu_1} = \begin{pmatrix} 5.00 \\ 10.0 \end{pmatrix} \quad \textrm{og} \quad \vec{\mu_2} = \begin{pmatrix} 12.5 \\ 30.8 \end{pmatrix} \]
De to nye midtpunkter ses indtegnet i figur 7 – igen markeret med et plus.
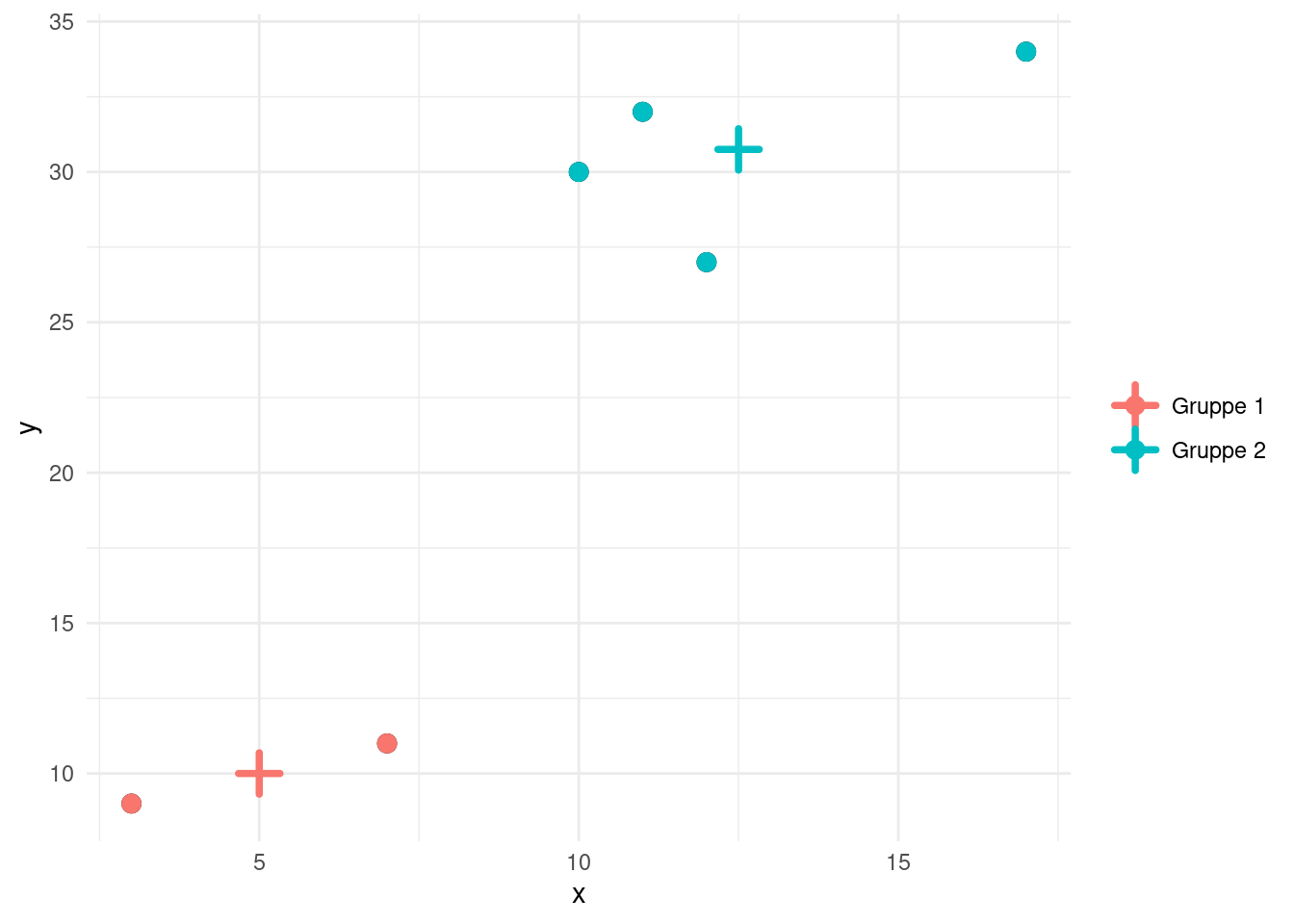
Vi kan nu igen udregne afstande fra alle punkter til de to nye midtpunkter og finde ud af om nogle af punkterne eventuelt skal skifte gruppe. Resultatet ses i tabel 3
| Afstand til \(\vec{\mu_1}\) | Afstand til \(\vec{\mu_2}\) | Opr. gruppe | Ny gruppe |
|---|---|---|---|
| 2.236 | 23.73 | 1 | 1 |
| 2.236 | 20.5 | 1 | 1 |
| 20.62 | 2.61 | 2 | 2 |
| 26.83 | 5.551 | 2 | 2 |
| 18.38 | 3.783 | 2 | 2 |
| 22.8 | 1.953 | 2 | 2 |
Vi kan nu se, at ingen af punkterne har skiftet gruppe, og algoritmen stopper derfor. Den endelige inddeling i grupper bliver derfor som vist i figur 7, hvilket nok også er den inddelingen, som vi ville have valgt bare ved at kigge på punkterne med det blotte øje.
Fornuftigt valg af midterpunkter og grupper
Vi vil nu argumentere for, hvorfor algoritmen virker. Vi starter med at se på, hvorfor det er fornuftigt at vælge midterpunkterne, som vi gør i trin 2 i algoritmen.
Da vi med algoritmen ønsker, at summen i (2) kaldet \(SUMMIDT\) skal minimeres, vil vi se, at valget af \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\) netop minimerer denne sum, når vi tænker, at grupperne er fastlagt.
Ved summen \(SUMMIDT\) har \(\vec{\mu_i}\) kun en effekt på delen hørende til gruppen \(S_i\), altså \[\sum_{\vec p\in S_i}\|\vec p-\vec{\mu_i}\|^2\]
For en vektor \(\vec v\), har vi følgende sammenhæng mellem længde og skalarprodukt/prikprodukt:
\[\|\vec v\|^2=\vec v\cdot \vec v \tag{3}\]
Dette gør, at vi kan omskrive vores sum for gruppen \(S_i\) til
\[\sum_{\vec p\in S_i}{(\vec p-\vec{\mu_i})\cdot (\vec p-\vec{\mu_i})}\] Skalarproduktet udregnes ved at tage summen af produktet af tilsvarende koordinater for vektorerne. Hvis vi lader \(p_m\) og \(\mu_{i,m}\) betegne det \(m\)’te koordinat af henholdsvis \(\vec p\) og \(\vec{\mu_i}\), så kan ovenstående sum skrives som
\[\sum_{\vec p\in S_{i}}\sum_{m=1}^{d}{(p_m-\mu_{i,m})\cdot (p_m-\mu_{i,m})} = \sum_{m=1}^{d} \sum_{\vec p\in S_{i}} {(p_m-\mu_{i,m})\cdot (p_m-\mu_{i,m})}\] Her vil valget af \(\mu_{i,m}\) kun have effekt på \[\sum_{\vec p\in S_{i}}{(p_m-\mu_{i,m})\cdot (p_m-\mu_{i,m})}\] I denne sum har vi ikke længere vektorer, og vi kan derfor benytte anden kvadratsætning til at få
\[\sum_{\vec p\in S_i}{(p_m^2-2\cdot p_m\cdot \mu_{i,m}+\mu_{i,m}^2)}\] For at finde ud af hvordan \(\mu_{i,m}\) skal vælges for at lave summen mindst mulig, differentieres ovenstående udtryk med hensyn til \(\mu_{i,m}\) og udtrykket sættes lig med \(0\):
\[\begin{align} \frac{\partial}{\partial \mu_{i,m}} \sum_{\vec p\in S_i}{(p_m^2-2\cdot p_m\cdot \mu_{i,m}+\mu_{i,m}^2)} &= \sum_{\vec p\in S_i} \frac{\partial}{\partial \mu_{i,m}} {(p_m^2-2\cdot p_m\cdot \mu_{i,m}+\mu_{i,m}^2)}\\ &= \sum_{\vec p\in S_i}{(-2\cdot p_m+2\cdot \mu_{i,m})}=0 \end{align}\]
Den sidste ligning kan omskrives til \[ \sum_{\vec p\in S_i}{2\cdot \mu_{i,m}} = \sum_{\vec p\in S_i}{2\cdot p_m}\] Ved division med \(2\) fås \[ \sum_{\vec p\in S_i}{\mu_{i,m}} = \sum_{\vec p\in S_i}{p_m}\]
Vi kan nu udnytte at hvert led i den første sum slet ikke afhænger af \(\vec p\), og da summen består af\(|S_i|\) led fås \[|S_i| \cdot \mu_{i,m}= \sum_{\vec p\in S_i}{p_m}\]
Altså er \[\mu_{i,m}=\frac{1}{|S_i|} \sum_{\vec p\in S_i}p_m\] Hvis dette valg tages for alle koordinater for \(\vec{\mu_i}\) svarer det til \[\vec{\mu_{i}}=\frac{1}{|S_i|} \sum_{\vec p\in S_i} \vec p\] som netop er den måde \(\vec{\mu_i}\) vælges på ved trin \(2\) i algoritmen.
Her glemte vi at argumentere for, at valget af \(\mu_{i,m}\) rent faktisk gav et lokalt minimum, men lidt løst kan man sige, at hvis \(\mu_{i,m}\) enten vælges alt for lille eller stor, vil afstanden og dermed også den kvadrerede afstand til punkterne i gruppen \(S_i\) blive store. Det kan selvfølgelig også bevises helt formelt.
Lad os nu se på valget af grupper ved trin \(3\) i algoritmen. For en punkt \(\vec p\) vælges den gruppe \(S_i\), hvor midtpunktet \(\vec{\mu_i}\) er tættest på \(\vec p\). Derved er det oplagt, at denne proces minimerer summen \(SUMMIDT\) i (2), når vi har fastholdt midterpunkterne \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\).
Når et punkt skifter gruppe vil \(SUMMIDT\) ikke længere være optimal i forhold til \(\vec{\mu_1},\vec{\mu_2},...,\vec{\mu_k}\) før de bliver opdateret igen. I algoritmen bliver disse to trin netop gentaget, indtil ingen punkter skifter gruppe, hvorved \(SUMMIDT\) har ramt et lokalt minimum i forhold til valg af gruppe for det enkelt punkt og valg af midterpunkt for hver gruppe.
Sammenhængen mellem SUMPAR og SUMMIDT
Nu vil vi endelig se på sammenhængen mellem de to summer \(SUMMIDT\) i (2) og \(SUMPAR\) i (1). Vi vil vise, at \[SUMPAR=2\cdot SUMMIDT\] når midterpunkterne er valgt på denne måde
\[ \vec{\mu_{i}}=\frac{1}{|S_i|} \sum_{\vec p\in S_i}\vec p \quad \quad \textrm{og derved} \quad \quad |S_i|\cdot \vec{\mu_{i}}=\sum_{\vec p\in S_i} \vec p \tag{4}\]
Det betyder, at hvis vi minimerer summen \(SUMMIDT\), så har vi også minimeret summen \(SUMPAR\), som var det vi oprindeligt ønskede.
Vi starter med at se på summen \(SUMPAR\) i (1) dog kun for en af grupperne \(S_a\) og uden faktoren \(\frac{1}{|S_i|}\). Altså ser vi på summen \[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p-\vec q\|^2 \tag{5}\]
Ved at bruge sammenhængen mellem længde af vektor og skalarprodukt får vi
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}(\vec p-\vec q)\cdot(\vec p-\vec q) \]
Her bruger vi nu, hvad der svarer til anden kvadratsætning for vektorer og vi omskriver tilbage til længder ved at bruge (3)
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}(\|\vec p\|^2+\|\vec q\|^2-2\cdot \vec p\cdot \vec q) \]
Denne dobbeltsum opdeles nu i tre dobbeltsummer og \(-2\) kan trækkes ud af den ene
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2+\sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec q\|^2-2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a} \vec p\cdot \vec q \]
De to første dobbeltsummer er faktisk ens og derfor får vi
\[ 2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2-2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q \tag{6}\]
For at komme videre med ovenstående vælger vi at se på dobbeltsummen
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q \] Den inderste sum afhænger ikke af \(\vec p\) og derfor kan \(\vec p\) sættes uden for sumtegnet4:
4 Husk på at den distributive regel også gælder for vektorer: \(\vec a \cdot \vec b + \vec a \cdot \vec c = \vec a \cdot \left (\vec b + \vec c \right)\)
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q = \sum_{\vec p\in S_a}\vec p\cdot \left (\sum_{\vec q\in S_a} \vec q \right ) \]
Fra valget af \(\vec{\mu_a}\) ved vi fra (4), at \(|S_a|\cdot \vec{\mu_{a}}=\sum_{\vec q \in S_a} \vec q\). Bruger vi det får vi
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q = \sum_{\vec p\in S_a}\vec p\cdot |S_a|\cdot \vec{\mu_{a}} \] Sætter vi \(|S_a|\cdot \vec{\mu_{a}}\) uden for summmen5 og udnytter ovenstående én gang til, får vi:
5 Bemærk, at vi igen her benytter den distributive regel for vektorer.
\[\begin{align} \sum_{\vec p\in S_a}\sum_{\vec q\in S_a} \vec p\cdot \vec q &= |S_a|\cdot \vec{\mu_{a}} \cdot \left ( \sum_{\vec p\in S_a}\vec p \right ) \\ &= \left ( |S_a|\cdot \vec{\mu_{a}} \right ) \cdot \left ( |S_a|\cdot \vec{\mu_{a}} \right ) \end{align}\]
Vi har nu et prikprodukt mellem to vektorer, som hver især er ganget med en skalar (her \(|S_a|\)). Bruger vi den kommutative lov6 for at gange med en skalar, får vi
6 Den kommutative lov siger, at \(k \cdot (\vec a \cdot \vec b) = (k \cdot\vec a) \cdot (\vec b) = (\vec a ) \cdot (k \cdot\vec b)\)
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a} \vec p\cdot \vec q = |S_a|^2 \cdot \| \vec{\mu_{a}} \|^2 \]
Det må derfor betyde, at \[ |S_a|^2\cdot \|\vec{\mu_a}\|^2-\sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q=0 \quad \Leftrightarrow \quad 2 \cdot |S_a|^2\cdot \|\vec{\mu_a}\|^2-2\cdot\sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q=0 \]
Da dette giver \(0\), kan det tilføjes til udtrykket i (6):
\[\begin{align} 2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2&-2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q = \\ 2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2-2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q &+ 2 \cdot |S_a|^2\cdot \|\vec{\mu_a}\|^2-2\cdot\sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q = \\ 2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2 + 2 \cdot |S_a|^2 &\cdot \|\vec{\mu_a}\|^2-4\cdot\sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\vec p\cdot \vec q \end{align}\]
I den sidste dobbeltsum kan \(\vec p\) igen tages ud af den inderste sum og vi kan igen udnytte at \(|S_a|\cdot \vec{\mu_{a}}=\sum_{\vec q \in S_a} \vec q\). Derved får vi
\[ 2\cdot \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p\|^2 + 2 \cdot |S_a|^2\cdot \|\vec{\mu_a}\|^2-4\cdot\sum_{\vec p\in S_a}\vec p\cdot |S_a|\cdot \vec{\mu_{a}} \]
Ved den første dobbeltsum ses det, at leddene ikke afhænger af \(\vec q\) og derfor er \(\sum_{\vec q\in S_a}\|\vec p\|^2 = |S_a| \cdot \|\vec p\|^2\) (fordi der er \(|S_a|\) led i summen). Det vil sige, at vi kan omskrive til
\[ 2\cdot \sum_{\vec p\in S_a}|S_a| \cdot \|\vec p\|^2 + 2 \cdot |S_a|^2\cdot \|\vec{\mu_a}\|^2-4\cdot\sum_{\vec p\in S_a}\vec p\cdot |S_a|\cdot \vec{\mu_{a}} \]
Vi kan nu se, at \(2 \cdot |S_a|\) indgår i alle led og vi kan derfor skrive:
\[ 2\cdot |S_a| \cdot \left ( \sum_{\vec p\in S_a} \|\vec p\|^2 + |S_a|\cdot \|\vec{\mu_a}\|^2-2\cdot\sum_{\vec p\in S_a}\vec p\cdot \vec{\mu_{a}} \right ) \]
Her kan \(|S_a|\cdot \|\mu_a\|^2\) laves om til en sum, hvor alle led er \(\|\mu_a\|^2\). Det vil sige
\[ 2\cdot |S_a| \cdot \left ( \sum_{\vec p\in S_a} \|\vec p\|^2 + \sum_{\vec p\in S_a} \|\vec{\mu_a}\|^2-2\cdot\sum_{\vec p\in S_a}\vec p\cdot \vec{\mu_{a}} \right ) \]
Hele udtrykket kan nu samles i én sum:
\[ 2\cdot |S_a| \sum_{\vec p\in S_a} \left ( \|\vec p\|^2 + \|\vec{\mu_a}\|^2-2\cdot\vec p\cdot \vec{\mu_{a}} \right ) \] Ved brug af anden kvadratsætning for vektorer kan dette omskrives til
\[ 2\cdot |S_a| \sum_{\vec p\in S_a} (\vec p - \vec{\mu_a}) \cdot (\vec p - \vec{\mu_a}) = 2\cdot |S_a| \sum_{\vec p\in S_a} \| \vec p - \vec{\mu_a} \|^2 \] Nu kan man jo godt have glemt, hvad det overhovedet var, vi var igang med at regne på! Men vi minder om, at det var udtrykket i (5). Det vil sige, at vi er kommet frem til, at
\[ \sum_{\vec p\in S_a}\sum_{\vec q\in S_a}\|\vec p-\vec q\|^2 = 2\cdot |S_a| \sum_{\vec p\in S_a} \| \vec p - \vec{\mu_a} \|^2 \] Eller skrevet på en anden måde:
\[ \frac{1}{|S_i|}\sum_{\vec p\in S_i}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2 = 2 \sum_{\vec p\in S_i} \| \vec p - \vec{\mu_i} \|^2 \] Summerer vi over alle \(k\) grupper får vi: \[ \sum_{i=1}^k \frac{1}{|S_i|}\sum_{\vec p\in S_i}\sum_{\vec q\in S_i}\|\vec p-\vec q\|^2 = 2 \sum_{i=1}^k \sum_{\vec p\in S_i} \| \vec p - \vec{\mu_i} \|^2 \] Sammenligner vi med (1) og (2) har vi netop vist, at
\[ SUMPAR = 2 \cdot SUMMIDT \]
Det vil altså sige, at hvis vi minimerer summen \(SUMMIDT\), så har vi også minimeret summen \(SUMPAR\), hvilket præcis var, hvad vi oprindeligt ønskede.
Opsummering/optimal løsning
Nu har vi set på selve algoritmen og fundet ud af, at den finder et lokalt minimum for summen \(SUMPAR\), som man ønsker minimeret. Der er dog ingen garanti for, at man opnår et globalt minimum, eller hvor lang tid algoritmen er om at finde en løsning.
Det er egentlig heller ikke noget problem at få lavet en algoritme, der finder en optimal løsning, problemet er blot, at den vil køre alt for langsomt. En sådan optimal algoritme kan laves ved blot at undersøge hver mulig inddeling i grupper og så finde den inddeling, der giver den mindste værdi af \(SUMPAR\). Dog vil det være sådan, at selv ved blot \(2\) grupper og \(100\) punkter vil der være \(2^{99}\) muligheder7, der skal tjekkes. At undersøge så mange muligheder er ikke praktisk muligt – selv ikke på en computer!
7 Fordi for hvert punkt kan punktet enten være i den ene eller den anden gruppe. Det giver i første omgang \(2^{100}\) grupper. Nu vil en inddeling hvor for eksempel punktet \(A\) og \(B\) er i gruppe \(1\), mens \(C\) er i gruppe \(2\) være den samme inddeling, som hvis \(C\) er i gruppe \(1\) og \(A\) og \(B\) er i gruppe \(2\). På grund af denne symmetri ender vi derfor samlet set med \(2^{100}/2=2^{99}\) grupper.
K-means ikke blot med punkter
Indtil videre har vi udelukkende set på data som værende punkter, hvor vi kan anvende euklidisk afstand for at måle afstanden mellem punkterne. Det kunne dog være langt mere interessant f.eks. at arbejde med mennesker og information om dem (f.eks. alder, køn, forbrug og så videre) og stadigvæk med et ønske om at inddele disse mennesker i et bestemt antal grupper, hvor der er stor ligmed mellem dem indenfor samme gruppe. Her skal man selvfølgelig have tænkt lidt over, hvordan man kommer fra mennesker til punkter og efterfølgende får noget, der svarer til euklidisk afstand. Det kan man læse meget mere om under feature-skalering.