Logistisk regression

I denne note skal vi se på logistisk regression. Måske har du allerede hørt begrebet "logistisk" i gymnasieundervisningen i forbindelse med logistisk vækst. Det er et helt andet emne end logistisk regression. Det eneste, de to emner umiddelbart har til fælles, er, at den logistiske funktion spiller en rolle begge steder. I slutningen af noten vil vi dog se et eksempel, hvor der alligevel er en sammenhæng mellem logistisk regression og logistisk vækst.

VIDEO: Introduktion

I videoen her giver vi en kort introduktion til noten.

Logistisk regression og hjerte-kar-sygdom

En helt central tankegang i mange metoder inden for kunstig intelligens er, at man på baggrund af en masse træningsdata for eksempel gerne vil afgøre om en patient er syg eller ej. En populær metode til det er at bruge et kunstigt neuralt netværk, som er en slags black-box-metode, og som du kan læse mere om her. Men hvis man lige præcis bruger et særligt slags neuralt netværk med et enkelt lag, er det faktisk ækvivalent med den meget ældre metode "logistisk regression", som vi gennemgår her, og som har den store fordel, at man kan forstå og fortolke modellen.

Logistisk regression, i den betydning vi betragter i denne note, bruges, når man gerne vil modellere, hvordan en sandsynlighed afhænger af en variabel. Som et eksempel forestiller vi os, at vi vil undersøge, hvordan sandsynligheden for at lide af hjerte-kar-sygdom afhænger af det systoliske blodtryk. Vi kigger derfor på et datasæt bestående af 2000 mennesker, som har fået målt deres blodtryk. Desuden har de fået undersøgt, om de lider af hjerte-kar-sygdom. Datasættet er fiktivt, men det er lavet til at ligne virkelige data¹. Vi kalder blodtrykket for $x$, mens vi lader $y$ være en variabel, der er $1$ hvis personen lider af hjertekarsygdom og $0$ ellers. På figur 1 har vi tegnet samhørende $x$- og $y$-værdier ind i et koordinatsystem for de første 200 personer i datasættet.

¹ De fleste mennesker har et systolisk blodtryk mellem 100 og 180 mmHg. I datasættet har vi genereret en masse mennesker med ekstremt højt eller lavt blodtryk for illustrationens skyld, selv om det er urealistisk i praksis.

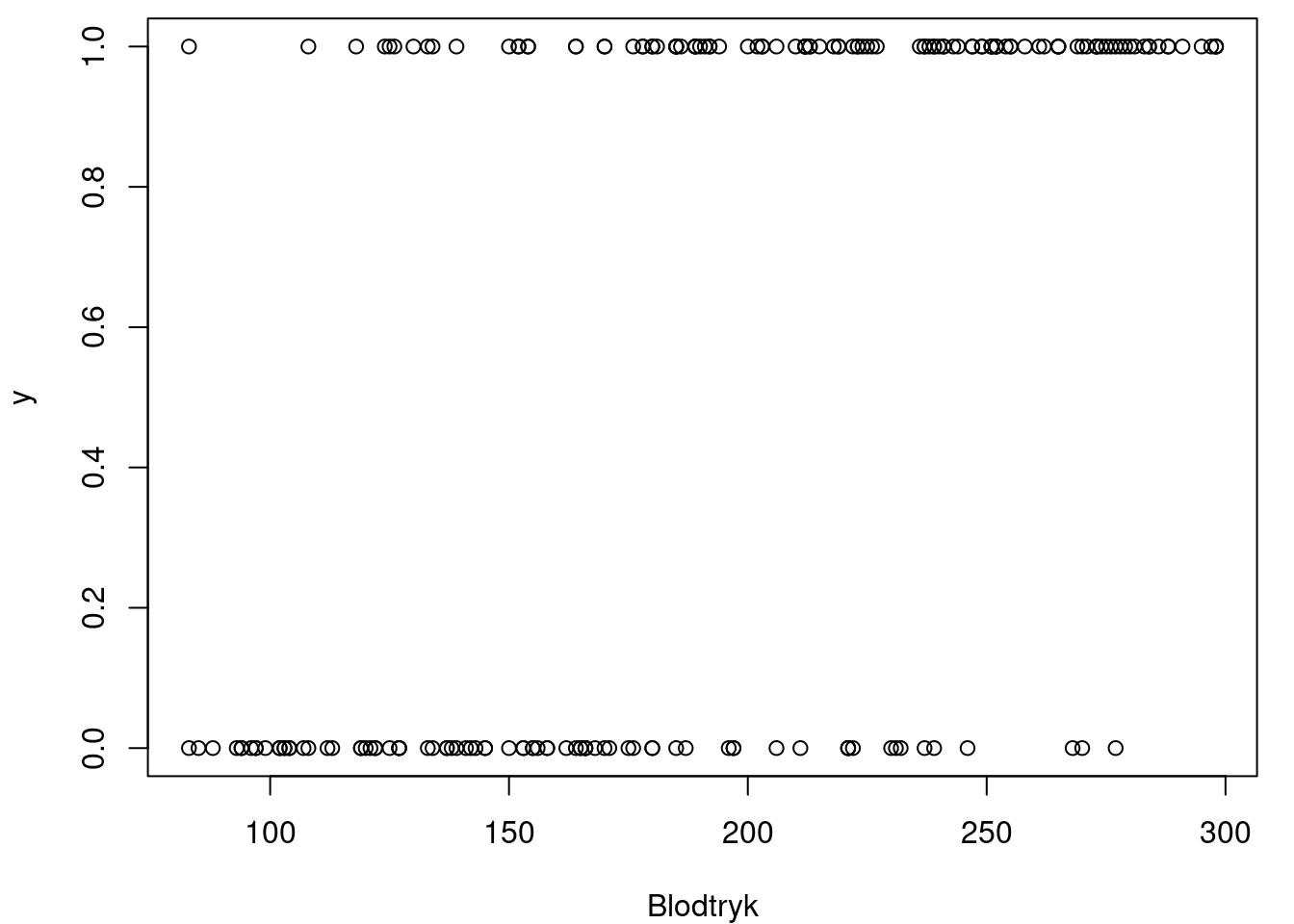
Figur 1: Her ses et plot af data med blodtryk på $x$-aksen og sygdomsstatus på $y$-aksen.

Det ses på figur 1, at der er flest personer med $y$-værdien 0, altså raske personer, blandt folk med lavt blodtryk, mens der er flest med $y$-værdien 1, svarende til syge, blandt folk med højt blodtryk. Ved de fleste blodtryksværdier er der dog både syge og raske, og det er svært at få et præcist overblik ud fra figuren.

Så hvordan kan man beskrive sammenhængen mellem $x$ og $y$? I stedet for at se direkte på sammenhængen mellem $x$ og $y$, vil vi se på hvordan sandsynligheden for hjerte-kar-sygdom afhænger af blodtrykket. Vi vil betragte denne sandsynlighed som en funktion $p(x)$ af blodtrykket $x$. Vi vil nu se på, hvordan man kan modellere denne funktion.

For at få en idé om, hvordan $p(x)$ kunne se ud, kigger vi på datasættet fra før. Vi inddeler blodtrykket i intervaller af længde 25 og tæller op, hvor mange syge og raske der er inden for hvert interval.

Blodtryk	Rask	Syg	Andel syge
(75,100]	168	29	0.147
(100,125]	195	45	0.188
(125,150]	143	63	0.306
(150,175]	152	105	0.409
(175,200]	93	135	0.592
(200,225]	57	136	0.705
(225,250]	46	179	0.796
(250,275]	25	204	0.891
(275,300]	19	206	0.916

Tabel 1: Tabel over syge og raske inden for forskellige blodtryksintervaller.

Desuden har vi beregnet, hvor stor en andel af patienterne inden for hvert interval, der lider af hjerte-kar-sygdom. Dette bruges som et estimat for sandsynligheden for hjerte-kar-sygdom i den gruppe. For eksempel er der 195 raske og 45 syge personer med et blodtryk i intervallet (100,125]. Sammenlagt er der $195+45 = 240$ personer i dette interval. Andelen af syge i denne gruppe er derfor \[ \frac{45}{240} \approx 0.188. \] På figur 2 har vi tegnet disse andele ind i et koordinatsystem. For hvert blodtryksinterval er midtpunktet for intervallet indtegnet som $x$-værdien, og andelen af syge er indtegnet som den tilhørende $y$-værdi².

² Det er klart, at vælger man nogle andre intervaller, så vil man få et lidt andet resultat. Bemærk også, at vi her bruger midtpunktet af intervallet i figur 2. Det er i modsætning til, når vi tegner sumkurver, hvor højre intervalendepunkt benyttes.

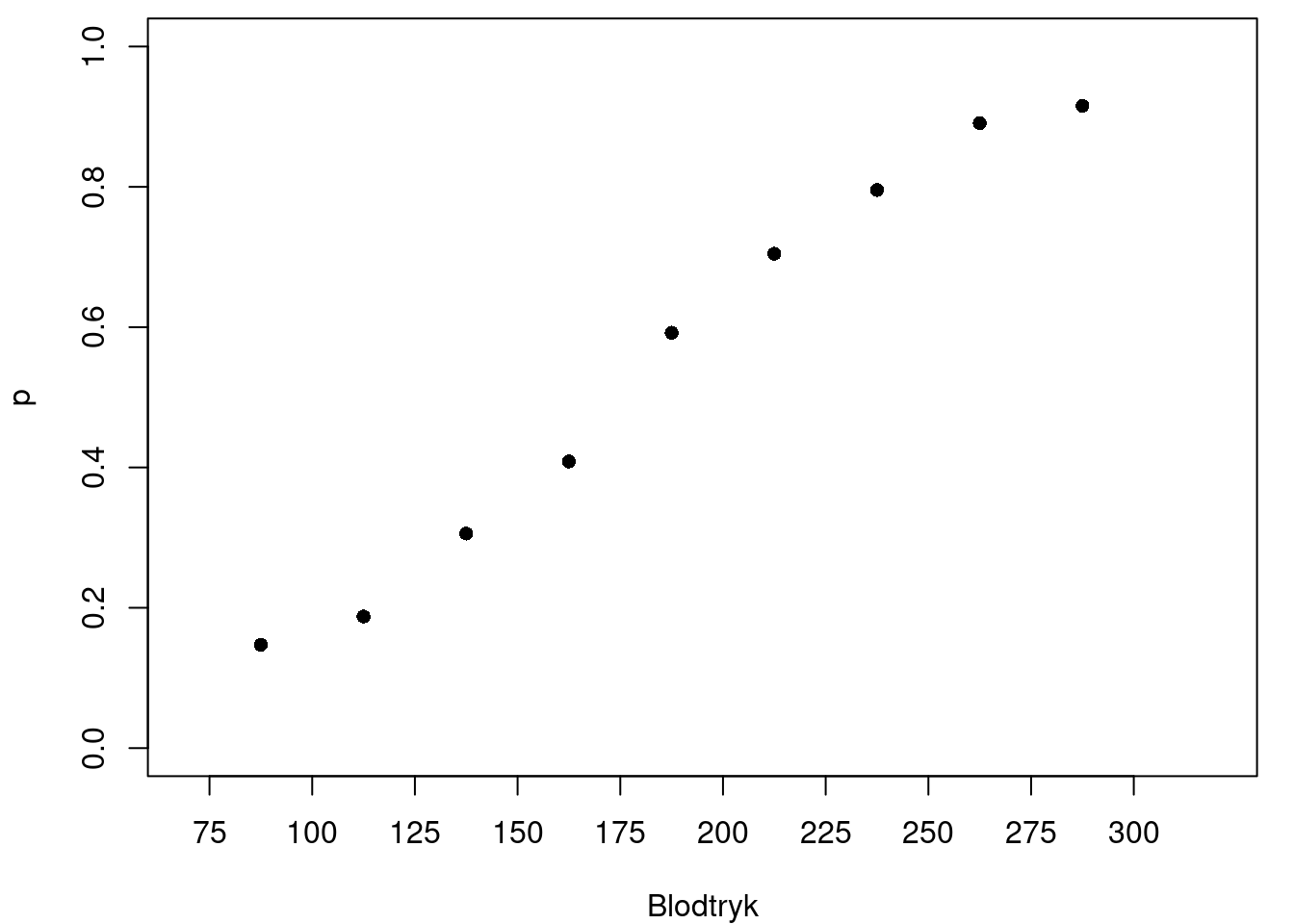
Figur 2: Andel syge inden for hvert blodtryksinterval.

Umiddelbart kunne det være fristende at lave lineær regression. Vi forestiller os altså en forskrift \[ p(x) = ax + b. \] På figur 3 har vi indtegnet den bedste rette linje i figur 2.

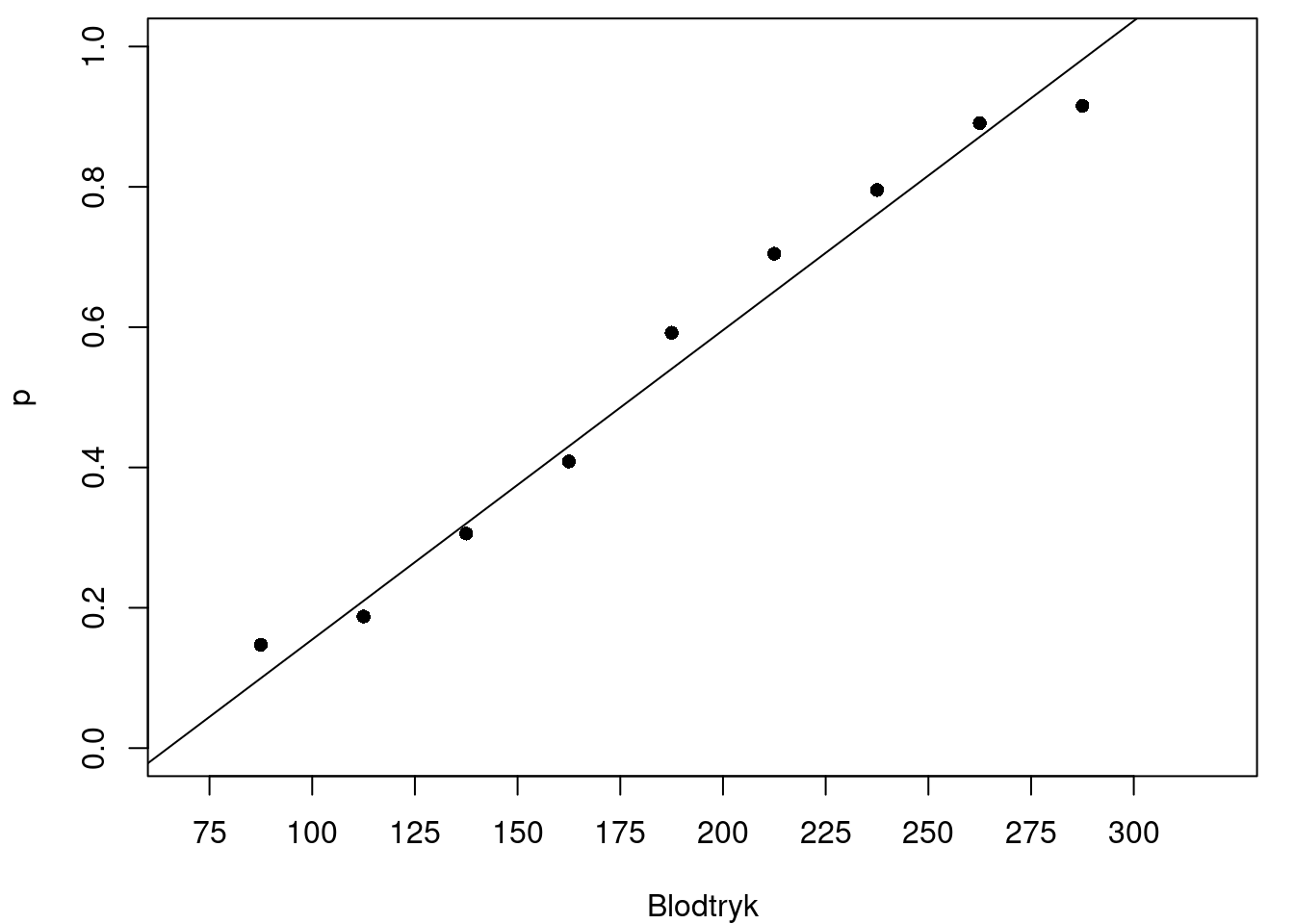
Figur 3: Grafen for $p(x)$ tilnærmet med en ret linje.

Der er et problem her: En sandsynlighed ligger altid mellem 0 og 1, men regressionslinjen ovenfor skærer $x$-aksen ved blodtryksværdier omkring 70. Det betyder, at sandsynligheden er negativ for blodtryk under 70. Tilsvarende får vi sandsynligheder, der er større end 1 ved blodtryk over 300. Det giver selvfølgelig ikke mening.

Hvis vi kigger på figur 3 igen, ser sammenhængen da heller ikke lineær ud, men snarere S-formet. I stedet for en ret linje, ville det give mening at lade $p$ være en funktion med en S-formet graf som indtegnet i figur 4.

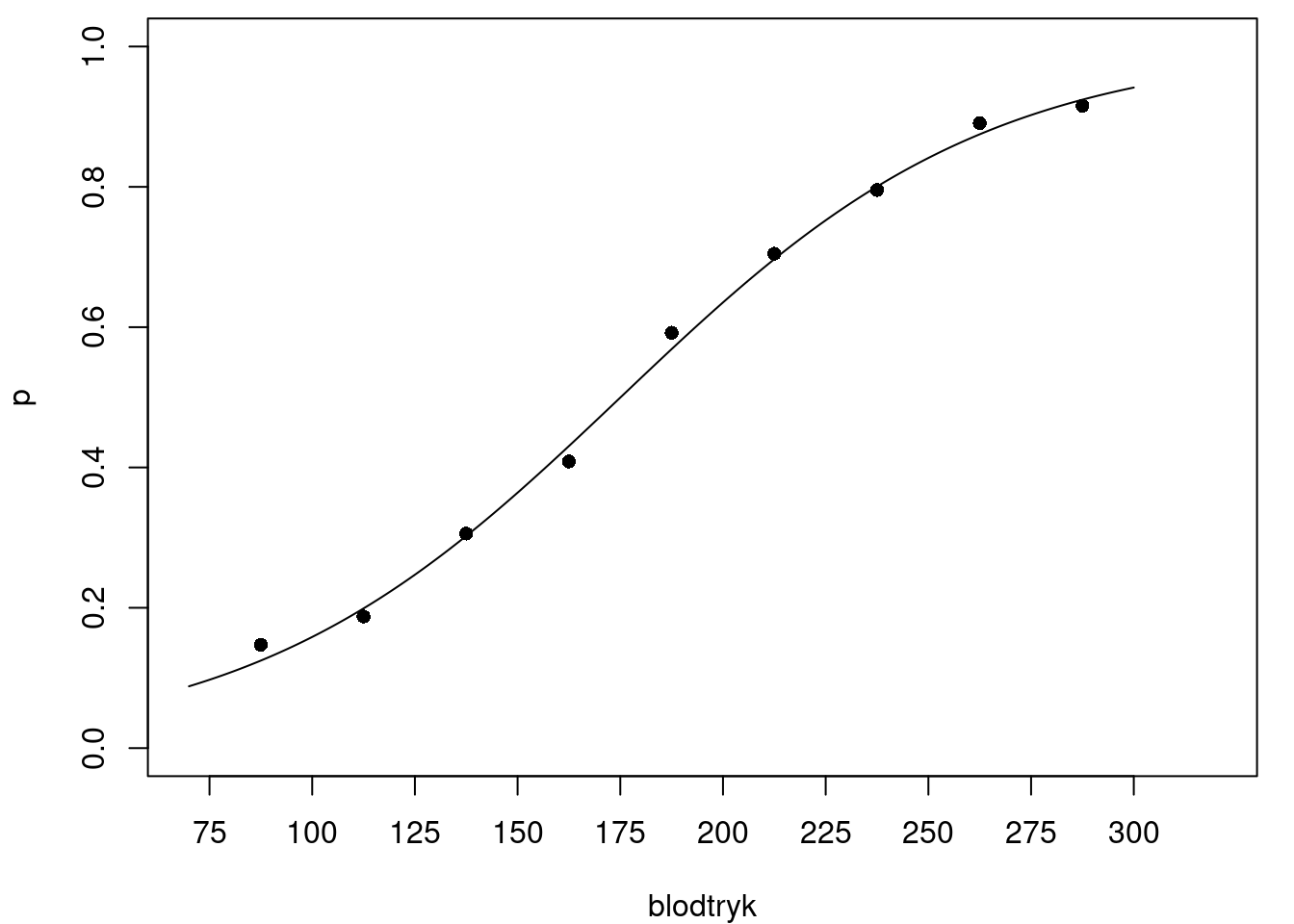
Figur 4: Graf for $p(x)$ tilnærmet med en S-formet kurve.

For at komme nærmere hvordan funktionsforskriften for $p$ skal se ud, viser det sig, at være smart at se på oddsene for sygdom i stedet for sandsynligheden³.

³ Du kender måske begrebet odds fra sportsgambling. Det er dog en anden betydning af ordet, end det vi bruger her. Inden for gambling angiver odds, hvor mange gange man får pengene igen, hvis en bestemt hændelse indtræffer(for eksempel at et bestemt hold vinder). Gambling odds er naturligvis også udregnet ud fra sandsynligheden for hændelsen, men de er altid justeret for at sikre, at bookmakeren vinder i det lange løb.

VIDEO: Dataeksemplet

I denne video præsenteres dataeksemplet.

Odds

Oddsene $O$ for en hændelse er defineret som sandsynligheden $p$ for hændelsen divideret med sandsynligheden for, at hændelsen ikke indtræffer (det kaldes også for komplementærhændelsen), som er $1-p$. Altså er \[ O=\frac{p}{1-p}. \] Odds måler således, hvor mange gange mere sandsynlig en hændelse er i forhold til komplementærhændelsen. Hvis for eksempel sandsynligheden for hjerte-kar-sygdom er $p=\frac{4}{5}$, så er odds for sygdom \[ O=\frac{\frac{4}{5}}{\frac{1}{5}} = 4. \] Det er altså fire gange så sandsynligt at være syg som at være rask.

For at få en lidt bedre fornemmelse for, hvordan odds fungerer, kan vi lave en tabel, der viser odds svarende til forskellige værdier af $p$:

$p$	$\frac{1}{5}$	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	$\frac{2}{3}$	$\frac{3}{4}$	$\frac{4}{5}$
$O$	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4

Læg her mærke til at jo større $p$ bliver, desto større bliver odds $O$ også.

Funktionen, der omdanner sandsynligheder til odds, har forskriften \[ O(p) = \frac{p}{1-p}. \] Definitionsmængden for $O$ er $]0,1[$. Bemærk, at $1$ ikke er med i definitionsmængden, fordi vi så vil komme til at dividere med $0$ i ovenstående udtryk. Vi tillader heller ikke, at $0$ er med i definitionsmængden. Der er ikke noget i vejen for at udregne odds til $0$ (det vil bare give $0$), men det hænger sammen med, at vi senere gerne vil tage logaritmen til odds, og logaritmen er som bekendt kun defineret for positive tal og altså ikke for $0$.

Grafen for $O$ er vist på figur 5.

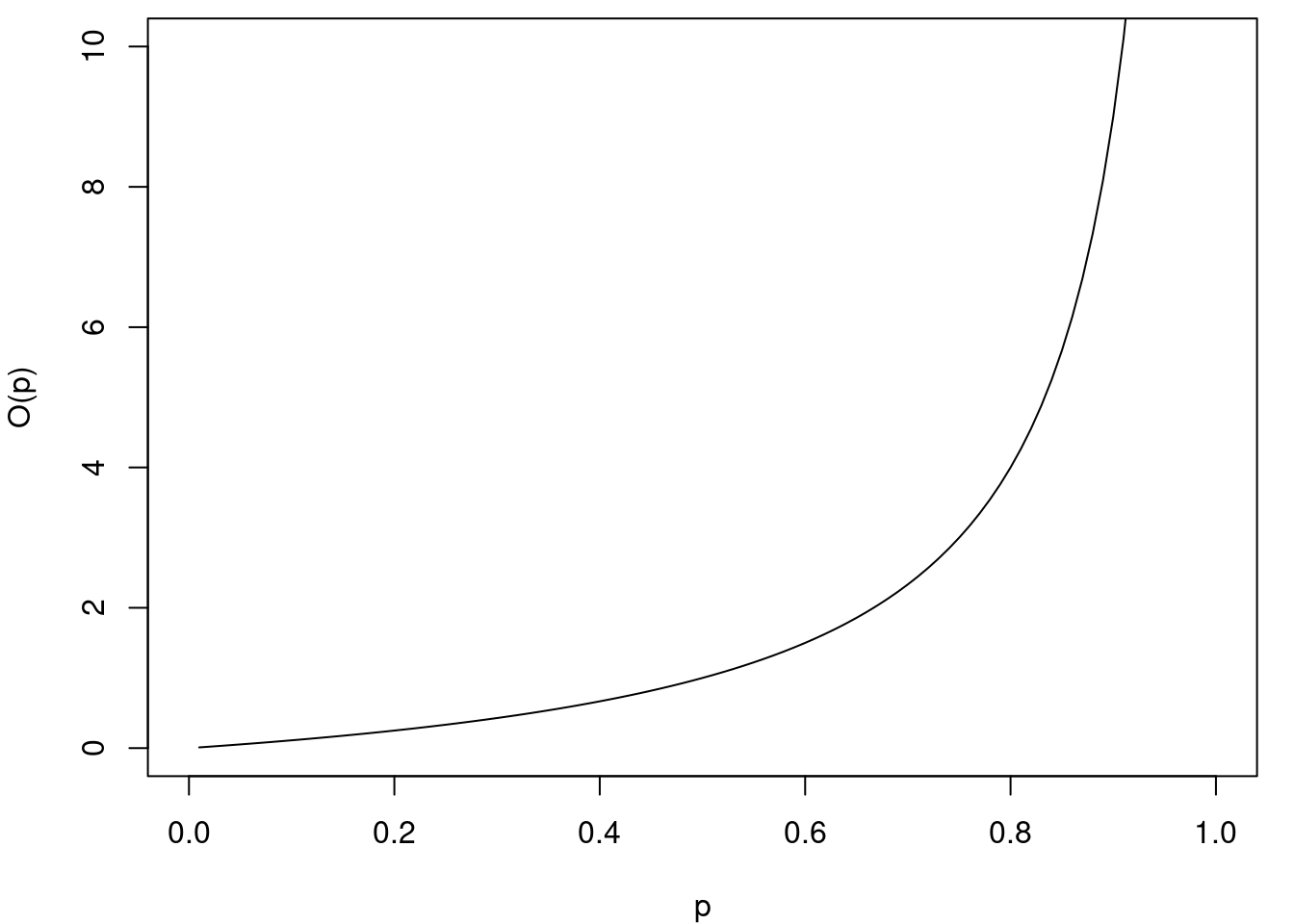
Vi kan se på figur 5, at odds-funktionen $O$ er voksende. Det kan også bevises ved at vise, at $O'(p)>0$ for alle værdier af $p$. Vi ser desuden, at $O(p)$ altid er positiv, da både tæller og nævner er positive. Når $p$ nærmer sig $0$, nærmer tælleren sig $0$, mens nævneren nærmer sig $1$, så $O(p)$ går mod $0$. Når $p$ nærmer sig $1$, nærmer tælleren sig $1$, og nævneren nærmer sig $0$, så hele brøken $O(p)$ går mod uendelig. Værdimængden for $O$ består derfor af alle de positive reelle tal.

VIDEO: Odds

Vi giver her en introduktion til begrebet odds.

Den logistiske regressionsmodel

I vores dataeksempel, hvor sandsynligheden for hjerte-kar-sygdom er en funktion $p(x)$, bliver oddsene for hjerte-kar-sygdom også en funktion af $x$ \[ O(p(x)) = \frac{p(x)}{1-p(x)}, \] hvor $x$ er blodtrykket.

På figur 6 vises dataeksemplet fra før, men nu har vi oddsene $O(p(x))$ på $y$-aksen.

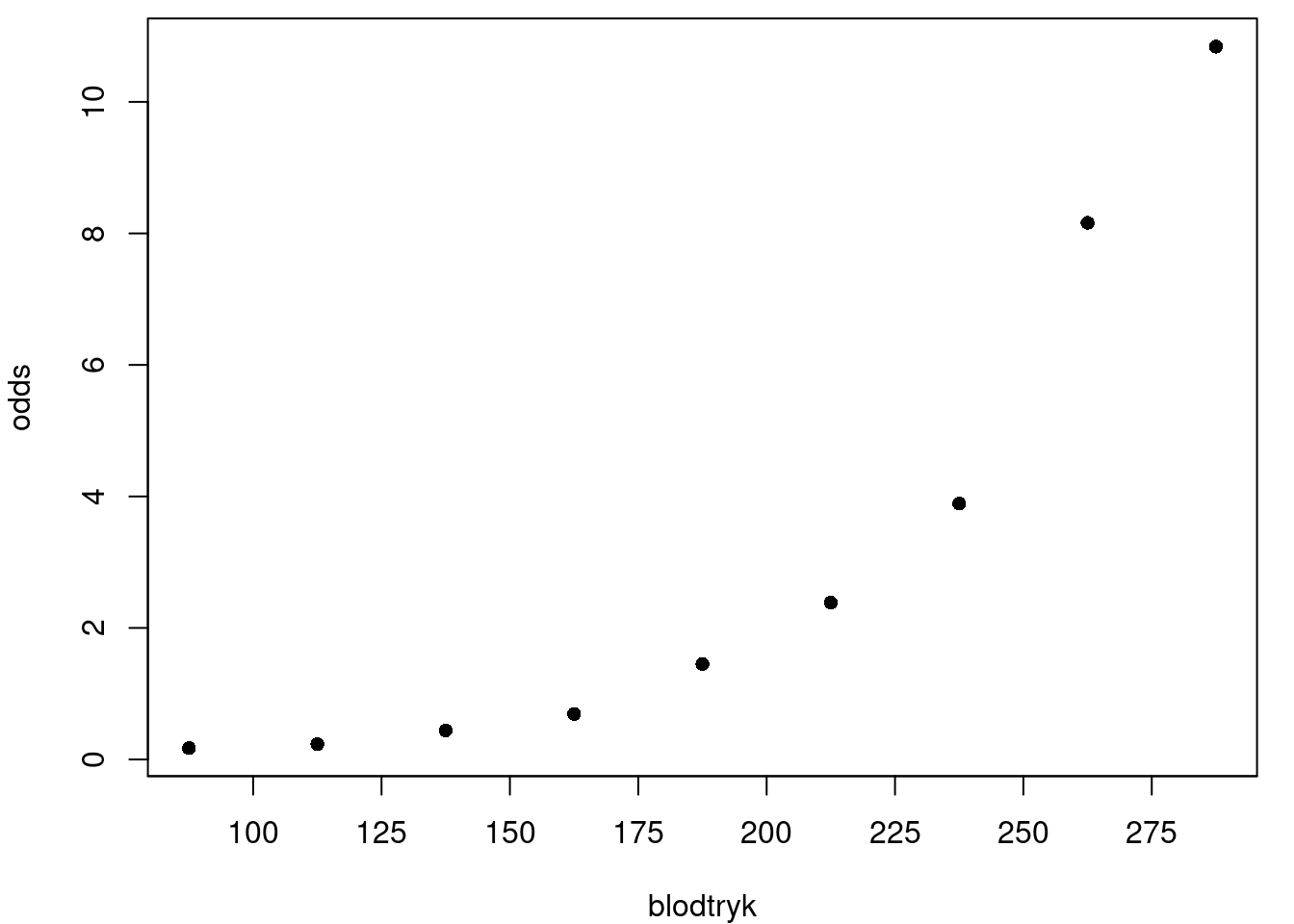
Figur 6: Odds for hjerte-kar-sygdom inden for de forskellige blodtryksintervaller.

Vi ser, at oddsene for sygdom stiger med blodtrykket. Det betyder derfor også, at sandsynligheden for sygdom stiger med blodtrykket. Kigger vi på grafen, ser tendensen ikke lineær ud. Det kunne derimod ligne en eksponentiel vækst. For at bekræfte dette, laver vi samme plot på figur 7, men nu med den naturlige logaritme til oddsene $\ln (O(p(x)))$ på $y$-aksen⁴.

⁴ Man kan nemlig vise, at hvis $y$ afhænger eksponentielt af $x$, så vil $\ln(y)$ afhænge lineært af $x$.

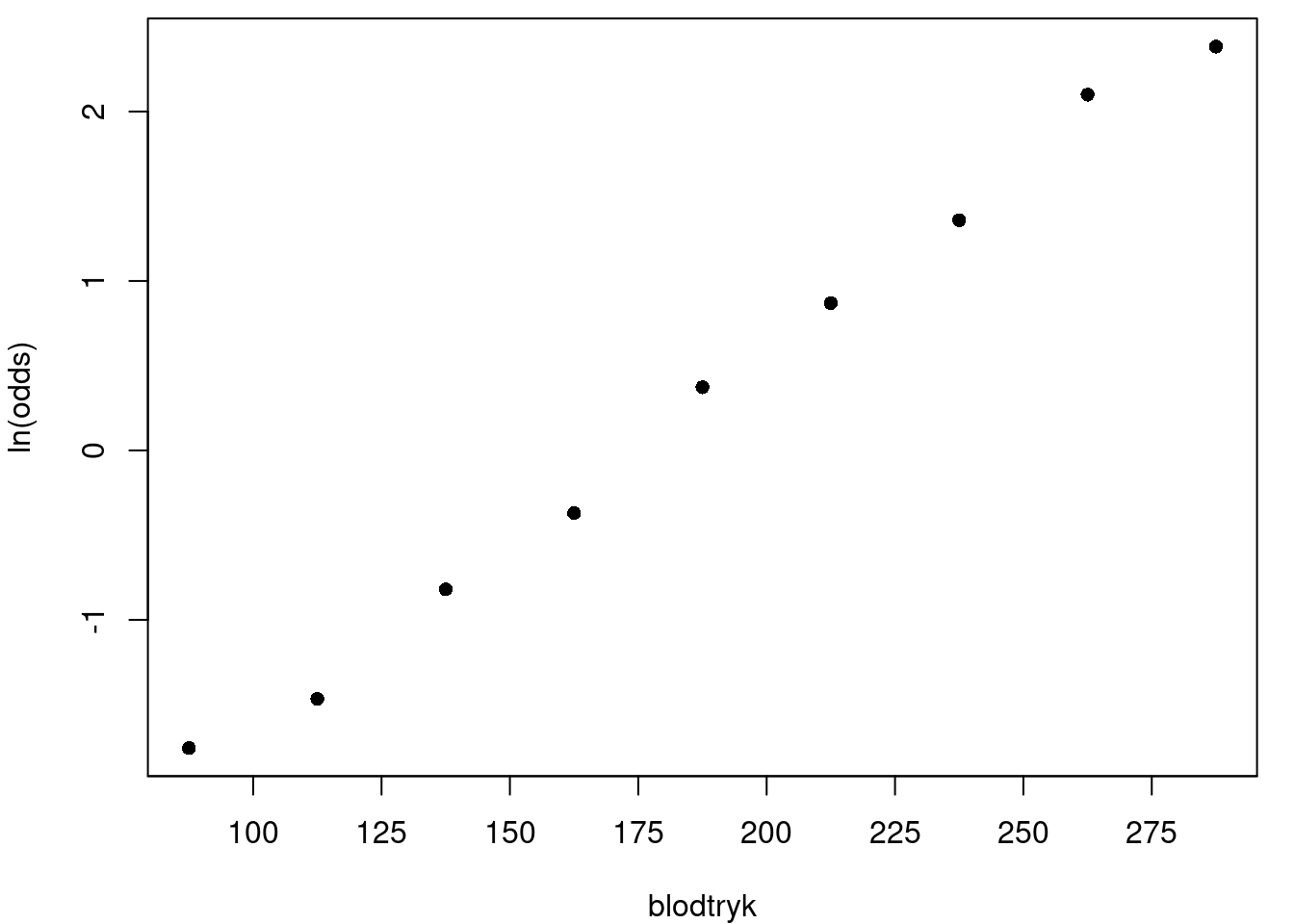
Figur 7: Den naturlige logaritme til odds for hjerte-kar-sygdom inden for de forskellige blodtryksintervaller.

Der ser nu ud til at være en lineær sammenhæng! Det kunne altså tyde på, at ln-oddsene afhænger lineært af $x$. Det leder os frem til følgende model for ln-oddsene: \[ \ln (O(p(x))) = ax + b. \tag{1}\] Denne model kaldes den logistiske regressionsmodel. Virkelige data følger ofte en logistisk regressionsmodel.

I næste afsnit ser vi på, hvordan man kan finde et funktionsudtryk for $p(x)$ i den logistiske regressionsmodel.

Logit-funktionen og den logistiske funktion

Når vi tager den naturlige logaritme til oddsene, får vi \[ \ln (O(p)) = \ln\left(\frac{p}{1-p}\right). \] Funktionen på højresiden kaldes $\text{logit}$ og er altså givet ved \[ \text{logit}(p) = \ln\left(\frac{p}{1-p}\right). \] Definitionsmængden for $\text{logit}$-funktionen er ligesom for oddsene $]0,1[$. Vi fandt tidligere, at værdimængden for oddsene består af alle de positive reelle tal. Dette er netop definitionsmængden for $\ln$. Værdimængden for $\text{logit}$ bliver derfor den samme som for $\ln$, nemlig alle de reelle tal. Grafen for $\text{logit}$ er vist på figur 8.

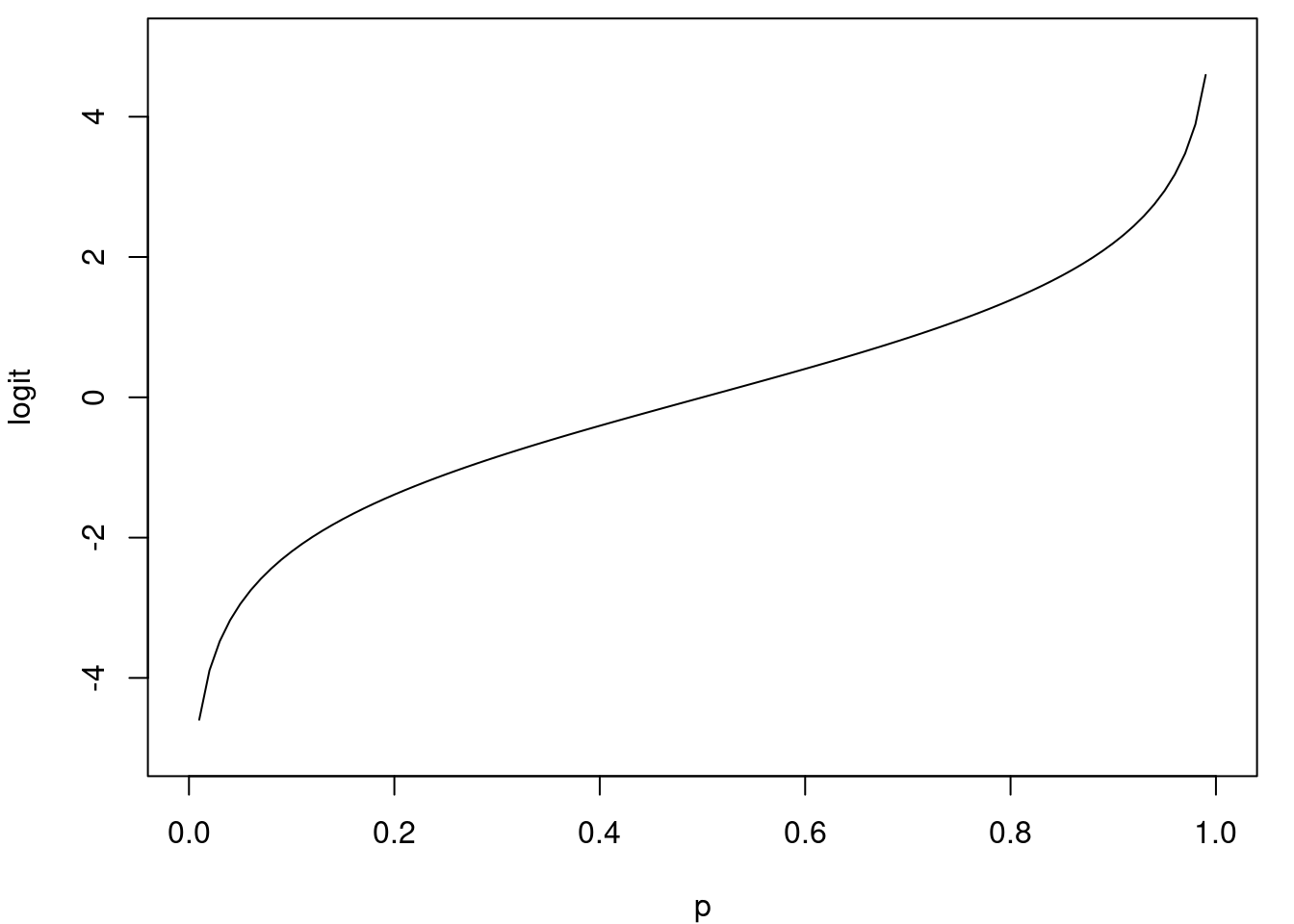
Den logistiske regressionsmodel i (1) kan skrives ved hjælp at $\text{logit}$-funtionen som \[ \text{logit}(p(x)) = \ln (O(p(x))) = ax + b. \tag{2}\] Egentlig var vi jo ude på at finde et udtryk for sandsynligheden $p(x)$ som funktion af $x$. Vi prøver derfor at isolere $p(x)$ i (2). For at gøre det, finder vi først den omvendte (eller inverse) funktion til $\text{logit}$. Vi antager derfor, at \[ y = \text{logit(p)} = \ln\left( \frac{p}{1-p} \right). \] Vi skal så isolere $p$ for at udtrykke $p$ som funktion af $y$. Vi tager først eksponentialfunktionen på begge sider af udtrykket og får \[ e^y = \frac{p}{1-p}. \] Så ganger vi med $(1-p)$ på begge sider. Det giver \[ e^y(1-p) =p. \] Hvis parentesen ophæves, får vi \[ e^y - p\cdot e^y =p. \]

Vi kan så lægge $p\cdot e^y$ til på begge sider og sætte $p$ uden for parantes. Det giver \[\begin{align*} e^y &= p \cdot e^y+p \\ e^y &= p\cdot (e^y+1). \end{align*}\] Endelig kan vi isolere $p$ og få \[ \frac{e^y}{e^y+1} =p. \] Her er $p$ egentlig isoleret, men vi kan vælge at forkorte brøken med $e^y$ for at få et andet udtryk for $p$ \[ p=\frac{\frac{e^y}{e^y}}{\frac{e^y+1}{e^y}}=\frac{\frac{e^y}{e^y}}{\frac{e^y}{e^y}+\frac{1}{e^y}} =\frac{1}{1+e^{-y}} . \]

Sammenlagt har vi vist, at den inverse funktion til logit er den standard logistiske funktion (også nogle gange kaldet sigmoid-funktionen) \[ f(y) = \frac{1}{1+e^{-y}}. \] Grafen for den standard logistiske funktion er indtegnet i figur 9. Vi ser, at grafen har en karakteristisk S-form, som vokser fra $0$ mod $1$.

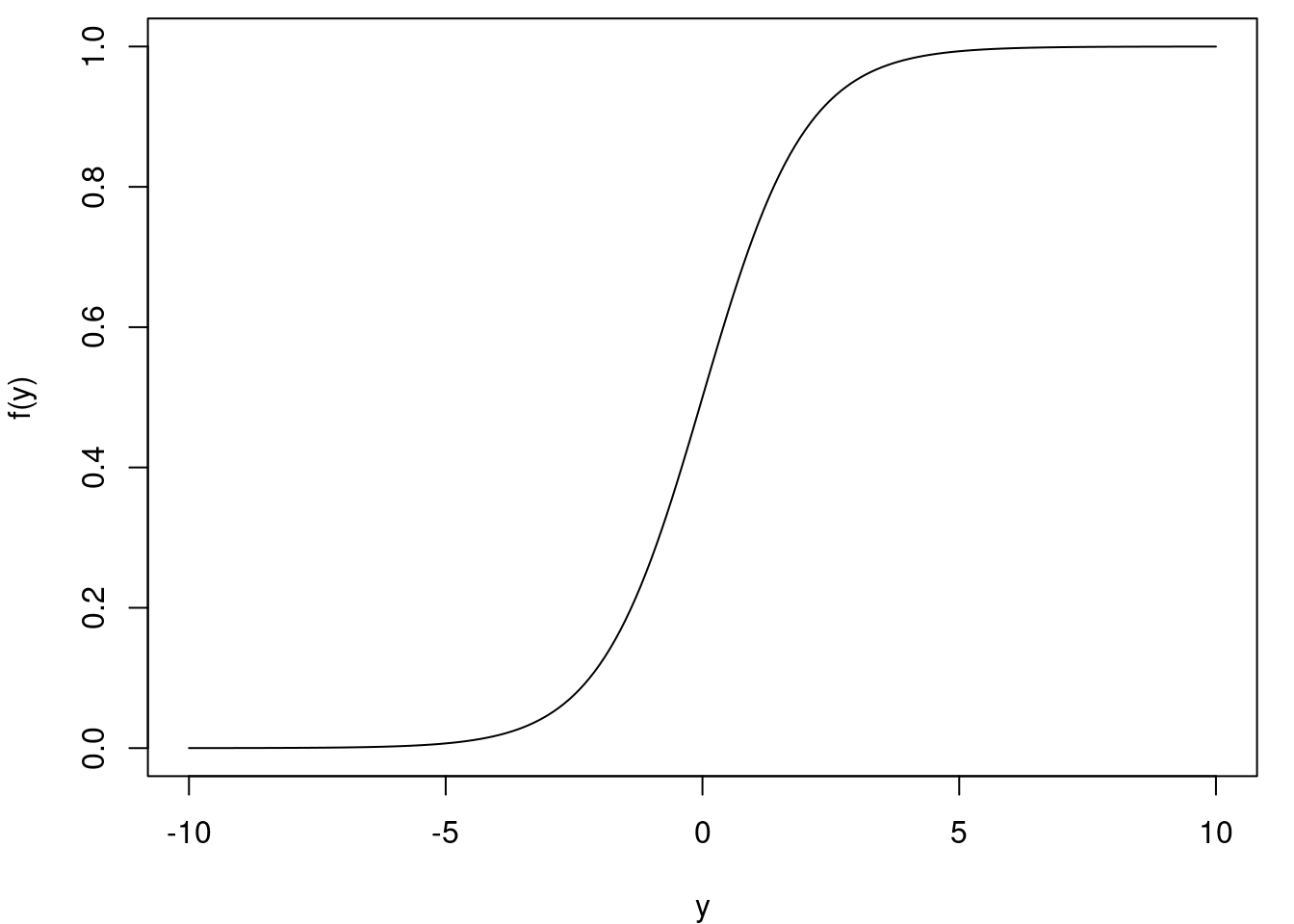
Figur 9: Grafen for den standard logistiske funktion

Bruger vi den inverse til $\text{logit}$ på begge sider af lighedstegnet i den logistiske regressionsmodel i (2), får vi isoleret $p(x)$ \[ p(x) = \frac{1}{1+e^{-(ax+b)}}. \tag{3}\] Det ligner altså den standard logistiske funktion, men med $(ax+b)$ indsat på $y$’s plads. Denne funktion kaldes den generelle logistiske funktion.

VIDEO: Den logistiske regressionsmodel og den logistiske funktion

En gennemgang af den logistiske regressionsmodel samt den logistiske funktion finder du i videoen her:

Fortolkning af parametrene i den logistiske regressionsmodel

Hvordan skal vi forstå betydningen af konstanterne $a$ og $b$ i den logistiske regressionsmodel? Hvis man har en funktion $f$, så svarer funktionen $f(ax)$ til, at væksthastigheden er blevet sat op med en faktor $a$. Alternativt kan man forestille sig, at $x$-aksen er blevet skaleret med en faktor $1/a$. Grafen for $f(x-k)$ svarer til, at man har forskudt grafen med $k$ enheder i $x$-aksens retning. Hvis man kombinerer disse, kan man indse, at $f(ax+b)$ svarer til først at øge væksthastigheden med en faktor $a$ og derefter forskyde grafen med $k=\frac{-b}{a}$ i $x$-aksens retning, idet \[ f(ax+b)=f\Big(a\cdot \Big(x-\Big(\frac{-b}{a}\Big)\Big)\Big). \]

Hvis man gør dette for den standard logistiske funktion, får man netop den generelle logistiske funktion \[ f(ax+b)= \frac{1}{1+e^{-(ax+b)}}. \] Sammenlignet med den standard logistiske funktion får man altså en $S$-formet kurve, der vokser $a$ gange så hurtigt og er forskudt med $\frac{-b}{a}$.

I app’en herunder ser du grafen for $f(x)=\frac{1}{1+e^{-(ax+b)}}$. Hvis du trækker i skyderne for $a$ og $b$, kan du se, hvordan kurven ændrer form. Den stiplede linje har ligning $x=\frac{-b}{a}$ og svarer altså til den vandrette forskydning af grafen for den standard logistiske funktion. På figuren er der desuden 9 punkter, som du kan få grafen til at passe bedst muligt med.

Figur 10: Eksperimenter med a og b for at forstå deres betydning for grafen. Når du har klikket på en skyder med musen, kan værdien også ændres med piletasterne, hvilket kan ske mere præcist.

I den logistiske regressionsmodel (3) er $p(x)$ givet ved en generel logistisk funktion. Det var en generel logistisk funktion, der blev brugt til at lave den S-formede kurve på figur 4.

En anden måde at fortolke konstanterne $a$ og $b$ på er ved at gå tilbage til at se på oddsene. For at få et udtryk for oddsene i den logistiske regressionsmodel, kan vi anvende eksponentialfunktionen på begge sider i (1) og få \[ O(x) = e^{ax + b} = e^b \cdot e^{ax}=e^b \cdot (e^{a})^x. \] Hvis $e^b$ kaldes $b_{ny}$, og $e^{a}$ kaldes $a_{ny}$, ses at \[ O(x)=b_{ny}\cdot a_{ny}^x \] er en eksponentiel udvikling med fremskrivningsfaktor $a_{ny}=e^a$. Derved vil odds for sygdom stige med $r=e^a-1$ procent, hver gang blodtrykket stiger med $1$mmHg. Hvis $a$ er positiv, er $e^a>1$, og oddsene vokser altså eksponentielt. Hvis derimod $a$ er negativ, er $e^a<1$, og dermed aftager oddsene eksponentielt.

Har vi f.eks. en logit model \[ \text{logit}(p(x))= -2 + 0.2x. \] så er den procentvist vækst i odds, når $x$ vokser med 1 \[ r = e^a-1 = e^{0.2}-1 \approx 0.2214028. \] Altså vokser odds med ca. 22%, når $x$ vokser med 1 i modellen.

I forbindelse med logistisk regression kaldes $e^a$ også for odds-ratioen. For at forstå hvorfor, kan vi forestille os to patienter, en med blodtryk $x_1$ og en med blodtryk $x_2$. De har dermed oddsene \[\begin{align*} O(x_1) &= e^b \cdot e^{ax_1}\\ O(x_2) &= e^b \cdot e^{ax_2}. \end{align*}\] Lad os se på forholdet (ratioen) mellem de to personers odds: \[ \frac{O(x_1)}{O(x_2)} = \frac{e^b \cdot e^{ax_1}}{ e^b \cdot e^{ax_2}} = \frac{e^{ax_1}}{e^{ax_2}} = e^{ax_1 - ax_2} = e^{a(x_1 - x_2)} = (e^{a} )^{x_1-x_2}. \] Forholdet mellem oddsene afhænger altså kun af forskellen $x_1 - x_2$ mellem de to personers blodtryk. Hvis person 1 er har et blodtryk, der er 1mmHg højere end person 2, bliver forholdet (ratioen) mellem oddsene lige præcis $e^a$.

VIDEO: Fortolkning af parametrene i modellen

I videoen her forklarer vi, hvordan parametrene i den logistiske regressionsmodel kan fortolkes.

Hvordan man bestemmer $a$ og $b$ ud fra data forklares i det følgende.

Maksimum likelihood estimation

I den logistiske regressionsmodel \[ \ln (O(x)) = \text{logit}(p(x)) = ax + b. \] indgår to ukendte konstanter $a$ og $b$. Hvis vi har et datasæt, hvordan finder vi så de værdier af $a$ og $b$, der passer bedst til vores data?

Ved at se på figur 7 kunne man fristes til at benytte lineær regression til at finde $a$ og $b$. Bemærk dog, at hvert punkt egentlig er beregnet ud fra fra flere observationer, som ikke har samme $x$-værdi. Med et lille datasæt ville det slet ikke være muligt at lave en intervalinddeling som i tabel 1, uden at der kommer meget få personer i nogle grupper. Begge dele gør, at de beregnede værdier af $\ln(O(x))$ bliver meget upræcise, og det samme gør estimaterne for $a$ og $b$ derfor.

I stedet benytter man som regel maksimum likelihood metoden, som er en teknik, der stammer fra statistikken. Kort fortalt er idéen at vælge de værdier af $a$ og $b$, der gør vores data så sandsynligt som muligt.

Lad os kalde punkterne i vores datasæt $(x_i,y_i)$, hvor $i=1,\ldots,n$ er en nummerering af datapunkterne. Her angiver $x_i$ altså blodtrykket hos den $i$’te person, og $y_i$ er en variabel, der antager værdien $1$ hvis $i$’te person har hjerte-kar-sygdom og er $0$ ellers. For hvert par $(x_i,y_i)$ kan vi nu forsøge at beregne sandsynligheden $p_i$ for at $i$’te person faktisk har den sygsomsstatus $y_i$, som vi observerer. Hvis den $i$’te person er syg, dvs. $y_i=1$, er $p_i$ altså sandsynligheden for at være syg, når blodtrykket er $x_i$, så \[ p_i= p(x_i) = \frac{ 1}{1 + e^{-(ax_i + b)}}. \tag{4}\] Hvis patienten er rask, altså $y_i=0$, er $p_i$ sandsynligheden for at være rask, når blodtrykket er $x_i$, det vil sige \[ p_i=1- p(x_i) = 1- \frac{ 1}{1 + e^{-(ax_i + b)}}. \tag{5}\] Vi kan opskrive et samlet udtryk for $p_i$ uden at opdele efter værdien af $y_i$, nemlig \[ p_i= p_i(x_i)^{y_i}(1-p(x_i))^{1-y_i}. \tag{6}\] For at indse dette, ser vi først på tilfældet $y_i=1$, hvor (6) giver \[ p_i = p(x_i)^{1} (1-p(x_i))^{0} = p(x_i), \] da $a^0=1$ for alle værdier af $a$.

For $y_i=0$ giver (6)
\[ p_i = p(x_i)^{0} (1-p(x_i))^{1} = 1-p(x_i). \] Det passer altså med formlerne i henholdsvis (4) og (5). Bemærk at $p_i$ afhænger af de ukendte værdier $a$ og $b$. Vi kan altså opfatte $p_i$ som en funktion af to variable $p_i(a,b)$.

Nu kigger vi på den samlede sandsynlighed for at observere netop de værdier $y_1,\ldots,y_n$, som vi faktisk har observeret, når vi ved at patienternes blodtryk er givet ved $x_1,\ldots,x_n$. Til det formål antager vi, at personerne i datasættet er uafhængige af hinanden⁵.

⁵ Afhængigheder kan for eksempel opstå, hvis mange af personerne er i familie med hinanden, går i klasse sammen eller bor i samme by. I så fald kan de have noget til fælles, der gør at deres $y$-værdier er mere ens end ellers. Familiemedlemmer kan fx have samme arvelige tendens til hjerte-kar-sygdom. Som regel forsøger man at undgå sådanne afhængigheder, når man indsamler data.

For at komme videre, er vi nødt til at vide lidt om uafhængighed af hændelser: Husk på at to hændelser $A$ og $B$ er uafhængige, hvis man kan finde sandsynligheden for fælleshændelsen $A\cap B$ (at $A$ og $B$ indtræffer på en gang) ved at gange de enkelte sandsynligheder sammen: \[ P(A\cap B) = P(A)\cdot P(B). \]

Uafhængighed af $n$ hændelser $A_1,\ldots,A_n$ betyder tilsvarende, at sandsynligheden for, at alle $n$ hændelser indtræffer på samme tid $A_1 \cap A_2 \cap \dotsm \cap A_n$, kan findes som et produkt af sandsynlighederne for de enkelte hændelser⁶ \[ P(A_1 \cap A_2 \cap \dotsm \cap A_n) = P(A_1)\cdot P(A_2) \cdot \dotsm \cdot P(A_n). \]

⁶ Desuden skal der gælde, at hver gang vi udtager $m$ ud af de $n$ hændelser, skal sandsynligheden for, at de $m$ hændelser indtræffer samtidig, kunne findes ved en tilsvarende produktformel, men dette skal vi ikke bruge i det følgende.

Vi vender nu tilbage til vores data og lader $A_1$ være hændelsen at første patient har sygdomsstatus $y_1$, $A_2$ være hændelsen at anden patient har sygdomsstatus $y_2$ og så videre. Bemærk, at $P(A_i)$ er det samme, som det vi tidligere kaldte $p_i(a,b)$. Hændelsen at vi observerer $y_1,\ldots,y_n$ på samme tid, er fælleshændelsen $A_1 \cap A_2 \cap \dotsm \cap A_n$. Da vi antog, at de $n$ personer er udvalgt uafhængigt af hinanden, kan vi bruge produktformlen: \[ P(A_1 \cap A_2 \cap \dotsm \cap A_n) = P(A_1) \cdot \dotsm \cdot P(A_n) = p_1(a,b) \cdot p_2(a,b)\cdot \dotsm \cdot p_n(a,b). \] Bemærk, at sandsynligheden for vores udfald $y_1,\ldots,y_n$ afhænger af $a$ og $b$. Den kan derfor betragtes som en funktion af to variable \[ L(a,b) = p_1(a,b) \cdot p_2(a,b)\cdot \dotsm \cdot p_n(a,b). \] Denne funktion kaldes likelihoodfunktionen. Idéen med maksimum likelihood metoden er at vælge de værdier af $a$ og $b$, der gør sandsynligheden $L(a,b)$ for det, vi har observeret så stor som mulig. Vi søger altså de $a$ og $b$, der maksimerer funktionen $L(a,b)$. I praksis vælger man som regel at maksimere $\ln(L(a,b))$, som kaldes for log-likelihoodfunktionen. Det kommer vi mere ind på i det følgende afsnit. På figur 11 er det vist, hvordan grafen for en log-likelihoodfunktion kunne se ud. Den viser altså logaritmen af sandsynligheden for vores observationer som funktion af $a$ og $b$. Det sorte punkt angiver, hvor funktionsværdien er størst. De tilhørende $a$- og $b$-koordinater er altså dem, der gør vores observationer mest sandsynlige.

Figur 11: Graf for en log-likelihoodfunktion. Det sorte punkt angiver, hvor funktionsværdien er størst.

Maksimum for $L(a,b)$ kan ikke beregnes eksakt. I stedet kan man bruge numeriske metoder, for eksempel gradient nedstigning, som du kan læse mere om her. Man kan også forsøge at finde kritiske punkter, altså punkter, hvor de partielt afledte er nul, ved hjælp af numeriske metoder. Det kan du læse mere om her. I praksis kan optimeringen foretages ved hjælp af Excel som forklaret nedenfor.

Bestemmelse af $a$ og $b$ med Excels problemløser-værktøj

Vi vil nu finde estimater for $a$ og $b$ ved hjælp af Excel. Først og fremmest skal man sørge for, at man har aktiveret problemløser-værktøjet. Det gøres på følgende måde:

Gå op under filer og vælg indstillinger.
Vælg derefter tilføjelsesprogrammer.
Nederst vælges Excel-tilføjelsesprogrammer. Tryk på udfør.
Vælg til sidst tilføjelsesprogrammet problemløser fra en liste.

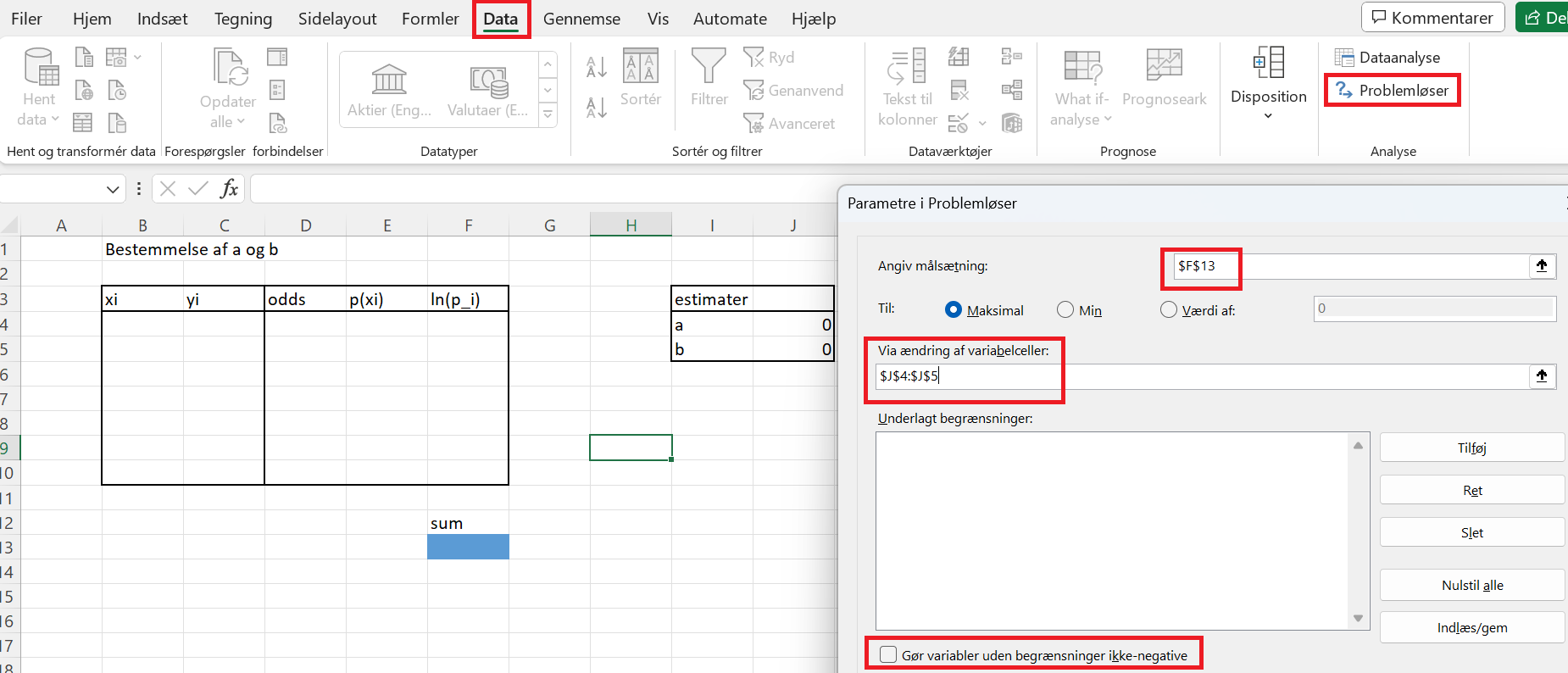
Illustration af Excel ark til bestemmelse af a og b samt brug af problemløser.

På billedet ses, hvordan man kan lave et lille regneark til at beregne de relevante størrelser. Der er lavet et par celler til de ukendte parametre $a$ og $b$, som med fordel kan sættes til 0 fra starten for at undgå numeriske problemer i Excel. Det oprindelige datasæt indsættes i søjlerne $x_i$ og $y_i$. I de næste søjler beregnes odds, $p(x_i)$ og $\ln(p_i)$ med formlerne⁷ \[\begin{align*} odds &= e^{ax_i + b}\\ p(x_i) &= \frac{e^{ax_i + b}}{1+e^{ax_i +b}} = \frac{odds}{1+odds}\\ \ln(p_i)&= {y_i}\cdot \ln(p(x_i))+(1-y_i)\cdot \ln(1-p(x_i)). \end{align*}\]

⁷ I Excel på dansk fås eksponentialfunktionen ved at skrive EKSP (og EXP i den engelske version). For at få den naturlige logaritmen skriver man LN i begge tilfælde.

Her er det vigtigt, at cellerne, der indeholder værdien af $a$ og $b$, benyttes når oddsene beregnes (det vil være smart med fastlåsning af referencerne, hvor man har $ foran både tal og bogstav ved reference). Til sidst finder man $l(a,b)$ i det blå felt ved at beregne summen af alle $\ln(p_i)$, som i formlen (9).

Nu mangler man bare at benytte problemløseren til at finde de værdier af $a$ og $b$, der gør værdien i det blå felt maksimal. På billedet er der vist med rød, hvor man finder problemløseren, og hvad der skal justeres. Målsætningen er den blå celle, der indeholder summen. Variabelcellerne er de to, der indeholder $a$ og $b$. Sørg for ikke at sætte flueben i boksen "Gør variabler uden begrænsninger ikke-negative". Tryk på løs.

Finder man $a$ og $b$ ved hjælp af maksimum likelihood metoden i vores dataeksempel, fås følgende funktionsudtryk for sandsynlighederne og oddsene \[ p(x) = \frac{1}{1+e^{-0.022 x +3.9}}, \qquad O(x)=e^{0.022 x - 3.9}. \]

Grafen for $p$ er vist på figur 4. Vi får en odds-ratio på $e^{0.022} \approx 1.022$. Odds for hjerte-kar-sygdom stiger derfor med en faktor 1.022 (altså 2.2%), for hver gang blodtrykket stiger med $1$ mmHg.

Yderligere omskrivning af likelihoodfunktionen

Vi ser nu lidt nærmere på, hvordan man selv kan finde $a$ og $b$, der maksimerer værdien af likelihoodfunktionen $L(a,b)$. Til det formål omskriver vi først likelihoodfunktionen til noget, der er lidt nemmere at regne på. Vi havde \[ L(a,b) = p_1(a,b) \cdot p_2(a,b)\cdot \dotsm \cdot p_n(a,b). \tag{7}\] Da $\ln(x)$ er en voksende funktion, vil $L(a,b)$ have maksimum for de samme værdier af $a$ og $b$ som den sammensatte funktion $l(a,b)=\ln(L(a,b))$. Det er altså nok at finde de værdier af $a$ og $b$, der maksimerer $l(a,b)$.

Tager vi den naturlige logaritme i (7) og bruger logaritmeregnereglen $\ln(a\cdot b) = \ln(a) + \ln(b)$, får vi \[ l(a,b)=\sum_{i=1}^n \ln(p_i(a,b)). \tag{8}\] Vi ser her, at logaritmen laver produktet i likelihoodfunktionen om til en sum – og summer er nemmere at regne på end produkter (for eksempel når vi senere skal differentiere). Bemærk, at det er denne funktion, som vi kalder for log-likelihoodfunktionen.

Vi fandt i (6), at \[ p_i(a,b)=p(x_i)^{y_i}\cdot (1-p(x_i))^{1-y_i}. \] Vi kan nu finde $\ln(p_i(a,b))$ ved først at benytte regnereglen $\ln(a\cdot b) = \ln(a) + \ln(b)$ og dernæst regnereglen $\ln(a^k)=k\cdot \ln(a)$. Det giver \[\begin{align*} \ln(p_i(a,b)) &= \ln\big(p(x_i)^{y_i}\big) + \ln\big((1-p(x_i))^{1-y_i}\big) \\ &= {y_i}\cdot \ln(p(x_i))+(1-y_i)\cdot \ln(1-p(x_i)) \end{align*}\] Samlet set får vi \[ \begin{aligned} l(a,b) &=\sum_{i=1}^n \ln(p_i(a,b)) \\ &= \sum_{i=1}^n\big( {y_i}\cdot \ln(p(x_i))+(1-y_i)\cdot \ln(1-p(x_i)) \big). \end{aligned} \tag{9}\] Dette udtryk kan man nemt selv udregne og maksimere ved hjælp af Excel.

VIDEO: Maksimum likelihood estimation

Idéen i maksimum likelihood estimation forklares i videoen herunder.

Multipel logistisk regression

I praksis er der selvfølgelig flere faktorer end blodtryk, der afgør ens risiko for hjerte-kar-sygdom. For eksempel stiger risikoen med alderen, ligesom rygning øger risikoen. Vi kan opstille en model, der inddrager alle tre variable på en gang. Lader vi $x_1$ betegne blodtryk, $x_2$ betegne alder, og $x_3$ betegne antal cigaretter, man ryger pr. dag, kan vi lave en model, hvor logaritmen til oddsene afhænger af alle tre variable: \[ \ln \left ( O(x_1,x_2,x_3) \right) = a_1x_1 + a_2x_2 +a_3x_3 + b. \] Nu er der fire ukendte konstanter $a_1$, $a_2$, $a_3$ og $b$ i modellen, som skal bestemmes ud fra data. Dette kaldes den multiple regressionsmodel. Ved at tage eksponentialfunktionen får vi en formel for oddsene \[ O(x_1,x_2,x_3) = e^{a_1x_1 + a_2x_2 +a_3x_3 + b}. \] Man kan også bruge den standard logistiske funktion og få en formel for sandsynligheden \[ p(x_1,x_2,x_3) = \frac{1}{1+e^{-(a_1x_1 + a_2x_2 +a_3x_3 + b)}}. \]

Hvordan skal vi forstå denne model? Jo, lad os forestille os en patient med alder $x_1$ og blodtryk $x_2$, som ryger $x_3$ cigaretter om dagen. Hvis vedkommende begynder at ryge $1$ cigaret mere om dagen (og vi forestiller os at alder og blodtryk er uændret) så vil odds-ratioen være \[ \begin{aligned} \frac{O(x_1,x_2,x_3+1)}{O(x_1,x_2,x_3)} &= \frac{ e^{a_1x_1 + a_2x_2 +a_3(x_3+1) + b}}{e^{a_1x_1 + a_2x_2 +a_3x_3 + b}} \\ &=\frac{e^{a_1x_1} \cdot e^{a_2x_2} \cdot e^{a_3x_3} \cdot e^{a_3} \cdot e^b}{e^{a_1x_1} \cdot e^{a_2x_2} \cdot e^{a_3x_3}\cdot e^b} \\ &=e^{a_3}. \end{aligned} \] Den ekstra daglige cigaret vil altså øge odds for sygdom med en faktor $e^{a_3}$. Tilsvarende har $e^{a_1}$ og $e^{a_2}$ fortolkninger som odds-ratioer, når henholdsvis blodtryk og alder stiger med 1, mens alle andre variable fastholdes. Selv om modellen tager alle tre variable i betragtning, giver odds-ratioerne et mål for den individuelle effekt af hver af de tre variable.

Maximum likelihood metoden kan igen benyttes til at estimere parametrene $a_1,a_2,a_3$ og $b$. Likelihoodfunktionen, som skal maksimeres, bliver nu til en funktion af fire variable. Vi vil ikke gå i detaljer med, hvordan denne maksimering finder sted.

Framingham datasættet er et rigtigt datasæt, der indeholder data for hjerte-kar-sygdom og de tre risikofaktorer $x_1$, $x_2$ og $x_3$. Estimerer man $a_1,a_2,a_3$ og $b$ på en udvalgt del af dette datasæt, får man \[ O(x_1,x_2,x_3) = e^{0.06x_1 + 0.02x_2 + 0.02x_3 -6.77 }. \] Odds for hjerte-kar-sygdom stiger således med en faktor $e^{0.02}\approx 1.02$ (altså med 2%), for hver cigaret man ryger om dagen. Tilsvarende stiger odds for sygdom med en faktor $e^{0.06}\approx 1.06$, for hvert år ældre man bliver, og med en faktor $e^{0.02}\approx 1.02$, for hver gang blodtrykket stiger med 1 mmHg.

Prædiktion

Når vi har fundet en god model for sammenhængen mellem sygdom og forskellige risikofaktorer, kan vi bruge den til at forudsige (prædiktere), om en ny patient er syg. Som eksempel kan vi se på den multiple regressionsmodel, hvor risikoen for hjerte-kar-sygdom var givet ved \[ p(x_1,x_2,x_3) = \frac{1}{1+e^{-(0.06x_1 + 0.02x_2 +0.02x_3 -6.77)}}, \] hvor $x_1$ var alderen, $x_2$ var blodtrykket, og $x_3$ var antal cigaretter.

Forestil dig nu, at vi får en ny patient med alderen $x_1$ og blodtrykket $x_2$, som ryger $x_3$ cigaretter om dagen. Vi kan beregne sandsynligheden $p(x_1,x_2,x_3)$ for, at patienten er syg ud fra vores model. Den mest oplagte prædiktionsregel er at prædiktere det mest sandsynlige:

Hvis $p(x_1,x_2,x_3)>1/2$: Patienten er syg.
Hvis $p(x_1,x_2,x_3)\leq 1/2$: Patienten er rask.

Lad os for eksempel sige, at vores patient er 30 år gammel, har et blodtryk på $145$ mmHg og ryger 7 cigaretter om dagen. Ifølge vores model vil hans risiko for hjerte-kar-sygdom være \[ p(30,145,7) = \frac{1}{1+e^{-(0.06\cdot 30 + 0.02\cdot 145 +0.02\cdot 7 -6.77)}}\approx 0.127. \] Hans risiko er på 12.7%. Hvis vi skal lave en prædiktion, vil vi sige, at han er rask, da dette vil være det mest sandsynlige.

I praksis kan der være et problem med altid at vælge det mest sandsynlige. Hvis man gerne vil kunne forudsige en meget sjælden sygdom, vil det ofte være sådan, at $p(x)\leq 1/2$ for alle patienter. Ingen ville blive diagnosticeret med sygdommen på denne måde - og så er prædiktionsalgoritmen jo ikke meget værd. Derfor vælger man ofte et lavere delepunkt end $p(x)=1/2$. Dermed kommer man til at fejldiagnosticere en hel del patienter. Til gengæld får man fanget flere af dem, der faktisk er syge.

Her på siden har vi flere eksempler på algoritmer, som vil kunne bruges til at prædiktere om patienter er syge eller raske, fx neurale netværk ⁸ og Bayes klassifikation. Fordelen ved at bruge logistisk regression er, at man ikke bare får en prædiktion, men også en model for, hvordan sandsynligheden $p(x)$ afhænger af variablen $x$. Dermed opnår man en indsigt i, hvordan sammenhængen mellem for eksempel blodtryk og hjerte-kar-sygdom er. Ved hjælp af odds-ratioer kan vi endda sætte tal på, hvordan odds for sygdom ændrer sig, når blodtrykket vokser. Dette er i modsætning til mange andre prædiktionsalgoritmer, der blot giver en prædiktion, uden at brugeren af algoritmen ved, hvor den kommer fra. Inden for medicin er det ofte vigtigt at kende baggrunden for en given prædiktion, så man kan forholde sig kritisk til resultatet og rådgive patienten om, hvordan man sænker risikoen for sygdom (for eksempel med blodtrykssænkende medicin). Til gengæld har de mere avancerede algoritmer, så som neurale netværk, mulighed for at give en mere præcis prædiktion.

⁸ Logistisk regression er i øvrigt et meget simpelt eksempel på et neuralt netværk, hvis man vælger af bruge cross-entropy funktionen som tabsfunktion.

Andre eksempler på anvendelser

Logistisk regression kan bruges til at modellere meget andet end sygdom. Forestil dig for eksempel en nyhedshjemmeside, der benytter cookies til at målrette reklamer. Hjemmesiden registrerer, hvor mange gange du har læst kulturnyheder, $x_1$, og hvor mange gange du har læst sportsnyheder, $x_2$, inden for den sidste måned. Desuden registrerer den, om du har klikket på en bestemt reklame for en ny biograffilm. Man kan bruge disse data til at finde en logistisk regressionsmodel for sandsynligheden $p(x_1,x_2)$ for, at en ny bruger klikker på reklamen. Med sådan en model kan man så prædiktere, om en ny bruger vil klikke på reklamen ud fra indsamlet data om brugerens forbrug af sports- og kulturnyheder. Reklamen vil så kun blive vist til brugeren, hvis det prædikteres, at brugeren rent faktisk vil klikke på reklamen.

Et andet eksempel kunne være en meningsmåling. Et mindre antal vælgere spørges, om de har tænkt sig at stemme på rød eller blå blok. Desuden noteres deres alder $x_1$ og årsindtægt $x_2$. Ud fra dette datasæt laves en model for sandsynligheden $p(x_1,x_2)$ for at stemme på rød blok som funktion af alder og årsindtægt. Ud fra modellen kan man så prædiktere, hvad resten af befolkningen har tænkt sig at stemme.

Hvis du vil læse mere om sammenhæng mellem logistisk regression og logistisk vækst, kan du folde boksen nedenfor ud.

Sammenhæng mellem logistisk regression og logistisk vækst

Hvis du har hørt om logistisk vækst og logistisk regression, spekulerer du måske over, om der er en sammenhæng mellem de to begreber. Vi skal nu se, at der i nogle anvendelser faktisk er en sammenhæng.

Lad os se på et eksempel med en smitsom sygdom, hvor infektionen aldrig forlader kroppen igen, og man kan fortsætte med at smitte andre resten af livet, når først man er blevet smittet. HIV og herpes er eksempler på sådanne sygdomme. Lad $I(x)$ betegne antallet af smittede efter $x$ dage ($I$ står for inficeret). Ifølge den klassiske SI-model, er væksthastigheden for $I$ proportional med både antallet af smittede $I(x)$ og antallet af raske $M-I(x)$, hvor $M$ er det samlede befolkningstal. Det vil sige \[ I'(x) = k I(x)(M-I(x)), \] hvor $k>0$ er en konstant. Denne ligning kaldes den logistiske differentialligning, og løsningen er givet ved \[ I(x)=\frac{M}{1+c\cdot e^{-M\cdot k\cdot x}}, \] hvor $c>0$ igen er en konstant, som kan bestemmes, hvis man kender antallet af smittede $I(0)$ til tiden $x=0$. Sætter vi $c=\exp(-b)$ og $a=Mk$, får vi \[ I(x)=\frac{M}{1+e^{-b}\cdot e^{-a\cdot x}} = \frac{M}{1+e^{-(a\cdot x+b)}}. \] På dag $x$ vil en tilfældigt udvalgt person have en sandsynlighed på $p(x)=I(x)/M$ for at være smittet. Denne sandsynlighed vil være beskrevet af en logistisk funktion \[ p(x)=\frac{I(x)}{M} = \frac{1}{1+e^{-(a\cdot x+b)}}. \] Dette genkender vi som en logistisk regressionsmodel for sandsynligheden $p(x)$.

For at bestemme $a$ og $b$, kunne man derfor lave et datasæt, hvor vi hver dag tager en test af en tilfældig person og ser, om personen er smittet eller rask. Derved får vi et datasæt med punkter $(x,y)$, hvor $x$ er antal dage, og $y$ er $0$ hvis personen er rask, eller $1$ hvis personen er smittet. Vi kan nu finde $a$ og $b$ ved at lave logistisk regression på dette datasæt og finde et udtryk for $p(x)$. Hvis vi gerne vil vide, hvor mange der faktisk er syge efter $x$ dage, ganger vi bare sandsynligheden for at være syg op med befolkningstallet \[ I(x)=M\cdot p(x)=\frac{M}{1+e^{-(a\cdot x+b)}}. \] Det er dog ikke ved alle eksempler, det er muligt at lave denne kobling mellem de to emner. Logistisk vækst vedrører en udvikling i tid, dvs. $x$-variablen skal angive tid. Desuden skal udviklingen foregå i en population af fast størrelse $M$.