Kunstige neurale netværk helt generelt
I denne note vil vi se på, hvordan man kan udvide det neurale netværk, vi så på i noten om neurale netværk til et netværk med et vilkårligt antal skjulte lag.
Fra bogstaver til indekser
Det står på nuværende tidspunkt nok klart for de fleste, at den notation, som vi har anvendt i noten om neurale netværk, er en lille smule tung. Der er bare rigtig mange bogstaver, og det kan være svært at huske om et givet bogstav betegner en outputværdi fra en neuron eller, om det er en vægt. Desuden skalerer notationen ufattelig dårligt! Forestil dig, at vi tilføjer \(2-3\) ekstra lag til vores netværk - det bliver svært at blive ved med at finde nye bogstaver!
Derfor griber man traditionelt set notationen i forbindelse med kunstige neurale netværk lidt anderledes an, så det skalerer bedre, og så det bliver nemmere at læse (i hvert tilfælde når man lige har vænnet sig til de ekstra indekser, som vi bliver nødt til at indføre).
Lad os se på netværket i figur 1. Dette netværk har \(3\) outputværdier i stedet for én, og der er ændret på antallet af neuroner i det ene af de skjulte lag i forhold til tidligere.
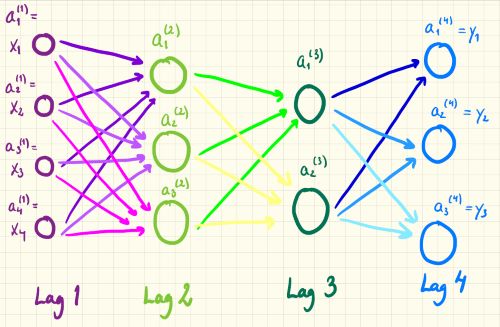
Hvert lag i netværket er nu nummeret fortløbende fra \(1\) til \(4\). Desuden giver vi nu en samlet betegnelse for den værdi, som hver neuron "spytter ud". F.eks. vil den \(3.\) neuron i det \(2.\) lag "outputte" eller "fyre" værdien \[ a_3^{(2)} \] Det vil altså sige, at det tal, som står hævet i parentesen1, refererer til laget og det tal, som er sænket, refererer til nummeret på rækken i det givne lag.
1 Bemærk, at vi i de andre noter har brugt en hævet parentes til at angive nummeret på et træningseksempel. Betydningen her er altså anderledes.
Bemærk også at inputværdierne i det første lag nu har to forskellige betegnelser for det samme: \[ x_i =a_i^{(1)} \] og tilsvarende har outputværdierne i det sidste og fjerde lag også to forskellige betegnelser: \[ y_i =a_i^{(4)} \] Lad os nu se på hvordan feedforward virker med vores nye notation. For det første er vi nødt til at være lidt smartere end tidligere i forhold til, hvad vi kalder vores vægte og bias. Der er tradition for, at man navngiver vægtene, som det ses på figur 2.
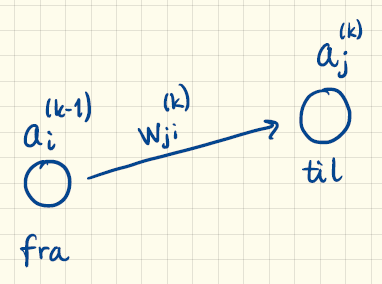
Her er tanken, at vi gerne vil beregne outputværdien fra den \(j\)’te neuron i det \(k\)’te lag. Det gør vi ved at vægte alle outputværdierne fra det foregående lag: (\(k-1\)). Den vægt, som vi ganger outputværdien fra den \(i\)’te neuron i det \((k-1)'te\) lag (\(a_i^{(k-1)}\)) med, og som skal bruges for at beregne \(a_j^{(k)}\), vælger vi at kalde for \[ w_{ji}^{(k)} \] Hvis man tænker på, at vi skal til række \(j\) i lag \(k\) fra række \(i\), så kan man måske huske på notationen sådan her: \[ w_{\textrm{til fra}}^{(\textrm{lag})} \] Se også hvordan det passer med figur 2.
Feedforward med indekser
Vi vil nu se på, hvordan de forskellige \(a_j^{(k)}\)-værdier beregnes. Det vil sige, at vi altså skal se på, hvordan de forskellige feedforward-ligninger ser ud med vores nye notation.
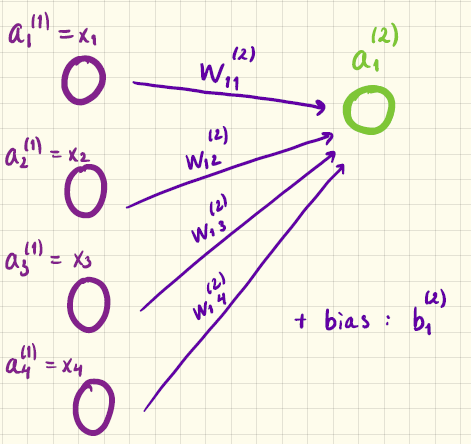
Lad os se på et konkret eksempel, så bliver det lidt nemmere at forholde sig til. Vi starter med at udregne outputværdien \(a_1^{(2)}\) for den første neuron i det andet lag. Denne neuron får input fra alle neuroner i det foregående lag (som her er inputlaget). Bruger vi den notation for vægtene, som vi lige har indført, så starter vi med at beregne: \[ z_1^{(2)} = w_{11}^{(2)} \cdot x_1 + w_{12}^{(2)} \cdot x_2 + w_{13}^{(2)} \cdot x_3 + w_{14}^{(2)} \cdot x_4 + b_1^{(2)} \] Der er to ting at bemærke her: 1) Vi vælger, at kalde udtrykket på højreside for \(z_1^{(2)}\) og, 2) vi har kaldt biasen for \(b_1^{(2)}\).
Bruger vi nu de mere generelle udtryk for inputværdierne \(a_1^{(1)}, a_2^{(1)}, \dots, a_4^{(1)}\) kan vi skrive: \[\begin{align} z_1^{(2)} &= w_{11}^{(2)} \cdot a_1^{(1)} + w_{12}^{(2)} \cdot a_2^{(1)} + w_{13}^{(2)} \cdot a_3^{(1)} + w_{14}^{(2)} \cdot a_4^{(1)} + b_1^{(2)} \\ &= \sum_{i=1}^{4} w_{1i}^{(2)} a_i^{(1)} + b_1^{(2)} \end{align}\] Og endelig finder vi outputværdien \(a_1^{(2)}\) for den første neuron i det andet lag ved som tidligere at anvende sigmoid-funktionen på ovenstående udtryk: \[\begin{align} a_1^{(2)} &= \sigma(z_1^{(2)}) \\ &= \sigma \left( \sum_{i=1}^{4} w_{1i}^{(2)} a_i^{(1)} + b_1^{(2)} \right) \end{align}\] Det her er faktisk notationsmæssigt selve idéen. Folder vi det ud til hele det andet lag får vi derfor:
Og vover vi pelsen, kan vi helt generelt skrive:
Fordelen ved denne notation er, at det nu er utrolig nemt at opskrive feedforward-ligningerne for lag 3 og 4 - det er blot nogle indekser, som skal ændres lidt. I det tredje lag er der to neuroner, hvis outputværdier beregnes på denne måde:
Og endelig beregnes outputtet fra hele netværket i det fjerde lag:
Det fremgår nu tydeligt, at feedforward-ligningerne er på fuldstændig samme form, og vi vil derfor helt generelt kunne skrive:
Når man bruger feedforward, starter man altså med at udregne outputværdierne for det første skjulte lag, dernæst for det andet skjulte lag og så videre, indtil man når til outputværdierne for selve netværket (deraf navnet: feedforward ). Bemærk her, at det ikke giver mening at udregne \(a_j^{(1)}\), fordi det svarer til inputværdierne til netværket.
Backpropagation med indekser
Lad os nu se på hvordan backpropagation fungerer. Vi skal altså have opskrevet vores opdateringsregler med den nye notation, og vi vil gribe det an, ligesom vi gjorde det i afsnittet Hvordan træner man et kunstigt neuralt netværk?. Nemlig ved at starte i det sidste lag (her lag \(4\)) og finde opdateringsreglerne for de vægte og bias, som har direkte indflydelse på outputværdierne fra lag \(4\).
Opdateringsregler for lag \(4\)
Vi er altså i første omgang på jagt efter \[ \frac{\partial E}{\partial w_{ji}^{(4)}} \quad \text{og} \quad \frac{\partial E}{\partial b_j^{(4)}}, \] for \(j \in \{1, 2, 3\}\), \(i \in \{1, 2\}\). Tabsfunktionen \(E\), som hører til netværket i figur 1, bliver her: \[ E=\frac{1}{2} \sum_{j=1}^3 \left( t_j-y_j \right)^2 = \frac{1}{2} \sum_{j=1}^3 \left( t_j-a_j^{(4)} \right)^2 \tag{3}\] hvor igen \(t_j\) er den ønskede target-værdi for den \(j\)’te outputneuron.
Lad os starte med at bestemme \(\frac{\partial E}{\partial w_{ji}^{(4)}}\). Vi må derfor først se på, hvordan \(w_{ji}^{(4)}\) påvirker tabsfunktionen \(E\). Da \(w_{ji}^{(4)}\) kun indgår i udtrykket for beregningen af \(z_j^{(4)}\), som igen bruges til beregningen af \(a_j^{(4)}\), som dernæst direkte påvirker tabsfunktionen, kan vi skrive: \[ w_{ji}^{(4)} \rightarrow z_j^{(4)} \rightarrow a_j^{(4)} \rightarrow E \] Bruger vi først kædereglen én gang, får vi derfor \[ \frac{\partial E}{\partial w_{ji}^{(4)}} = \frac{\partial E}{\partial z_j^{(4)}} \cdot \frac{\partial z_j^{(4)}}{\partial w_{ji}^{(4)}} \tag{4}\] og bruges kædereglen igen, kan første faktor udfoldes yderligere \[ \frac{\partial E}{\partial z_j^{(4)}} = \frac{\partial E}{\partial a_j^{(4)}} \cdot \frac{\partial a_j^{(4)}}{\partial z_j^{(4)}} \] Lad os starte med at udregne \(\frac{\partial E}{\partial z_j^{(4)}}\) ved at udregne hver faktor på højresiden i ovenstående udtryk for sig. Fra (3) får vi, at \[ E=\frac{1}{2} \sum_{j=1}^3 \left( t_j-a_j^{(4)} \right)^2 = \frac{1}{2} \left( \left( t_1-a_1^{(4)} \right)^2 + \left( t_2-a_2^{(4)} \right)^2+ \left( t_3-a_3^{(4)}\right)^2 \right) \] Hvis vi f.eks. skal differentiere ovenstående med hensyn til \(a_2^{(4)}\), kan vi se at alle de led, som ikke indeholder \(a_2^{(4)}\), vil være at betragte som konstanter, når vi differentierer - og når vi differentierer konstanter, får vi som bekendt \(0\). Derfor får vi, at \[ \frac{\partial E}{\partial a_2^{(4)}} = \frac{1}{2}\cdot 2 \cdot (t_2-a_2^{(4)})\cdot (-1) = -(t_2-a_2^{(4)}) \] På tilsvarende vis har vi derfor generelt, at \[ \frac{\partial E}{\partial a_j^{(4)}} = -(t_j-a_j^{(4)}) \tag{5}\] Vi ved også, at \[ a_j^{(4)} = \sigma(z_j^{(4)}) \] Og bruger vi endnu en gang, at sigmoid-funktionen differentieret er \(\sigma'(x)=\sigma(x)(1-\sigma(x))\), får vi, at \[ \frac{\partial a_j^{(4)}}{\partial z_j^{(4)}} = \sigma'(z_j^{(4)})= \sigma(z_j^{(4)}) \cdot (1-\sigma(z_j^{(4)}))= a_j^{(4)}\cdot (1-a_j^{(4)}) \tag{6}\] Indtil videre har vi altså, at \[\begin{align} \frac{\partial E}{\partial z_j^{(4)}} &= \frac{\partial E}{\partial a_j^{(4)}} \cdot \frac{\partial a_j^{(4)}}{\partial z_j^{(4)}} \\ &=-(t_j-a_j^{(4)}) \cdot a_j^{(4)}\cdot (1-a_j^{(4)}) \end{align}\] I forhold til det videre arbejde viser det sig hensigtsmæssigt, at lave en samlet betegnelse for \[\begin{align} \frac{\partial E}{\partial z_j^{(4)}} &=-(t_j-a_j^{(4)}) \cdot a_j^{(4)}\cdot (1-a_j^{(4)}) \end{align}\] Vi sætter derfor \[ \delta_j^{(4)} = \frac{\partial E}{\partial z_j^{(4)}} = -(t_j-a_j^{(4)}) \cdot a_j^{(4)} \cdot (1-a_j^{(4)}) \] Udtrykket \(\delta_j^{(4)}\) kalder man også for fejlleddet for det fjerde lag, men det kommer vi tilbage til senere.
Vi har nu fundet den første faktor i (4), og mangler derfor kun at bestemme \(\frac{\partial z_j^{(4)}}{\partial w_{ji}^{(4)}}\). Bruger vi (2) ser vi, at \[ z_j^{(4)} = \sum_{i=1}^{2} w_{ji}^{(4)} a_i^{(3)} + b_j^{(4)} = w_{j1}^{(4)} a_1^{(3)}+ w_{j2}^{(4)} a_2^{(3)} + b_j^{(4)} \] Skal vi f.eks. differentiere dette udtryk med hensyn til \(w_{j1}^{(4)}\), får vi (fordi de fleste led i ovenstående, vil være at betragte som konstanter) \[ \frac{\partial z_j^{(4)}}{\partial w_{j1}^{(4)}} = a_1^{(3)} \] Og helt tilsvarende hvis vi differentierer med hensyn til \(w_{j2}^{(4)}\), får vi \[ \frac{\partial z_j^{(4)}}{\partial w_{j2}^{(4)}} = a_2^{(3)} \] Generelt har vi derfor, at \[ \frac{\partial z_j^{(4)}}{\partial w_{ji}^{(4)}} = a_i^{(3)} \tag{7}\]
Samler vi nu de tre udtryk, som vi netop har udledt og indsætter i (4) får vi \[ \frac{\partial E}{\partial w_{ji}^{(4)}} = -(t_j-a_j^{(4)}) \cdot a_j^{(4)} \cdot (1-a_j^{(4)}) \cdot a_i^{(3)} \] og med den lidt kortere notation, som vi indførte ovenfor, kan vi nu skrive \[ \frac{\partial E}{\partial w_{ji}^{(4)}} = \delta_j^{(4)} \cdot a_i^{(3)} \] For at finde opdateringsreglerne for biasene, må vi først bestemme de partielle afledede af \(E\) med hensyn til \(b_j^{(4)}\). På helt tilsvarende vis får vi, at \[ \frac{\partial E}{\partial b_j^{(4)}} = \frac{\partial E}{\partial z_j^{(4)}} \cdot \frac{\partial z_j^{(4)}}{\partial b_j^{(4)}} \] Vi ved allerede, at \[\begin{align} \frac{\partial E}{\partial z_j^{(4)}} = \delta_j^{(4)} \end{align}\] og ser man på ligningen i (2), ses det nemt, at \[ \frac{\partial z_j^{(4)}}{\partial b_j^{(4)}} = 1 \] og derfor har vi, at \[ \frac{\partial E}{\partial b_j^{(4)}} =\delta_j^{(4)} \] Opdateringsreglerne for de vægte og bias, som hører til outputlaget (lag \(4\)) er derfor \[ w_{ji}^{(4)} \leftarrow w_{ji}^{(4)} - \eta \cdot \frac{\partial E}{\partial w_{ji}^{(4)}} = w_{ji}^{(4)} - \eta \cdot \delta_j^{(4)} \cdot a_i^{(3)} \] og \[ b_j^{(4)} \leftarrow b_j^{(4)} - \eta \cdot \frac{\partial E}{\partial b_j^{(4)}} = b_j^{(4)} - \eta \cdot \delta_j^{(4)} \] Vi kan altså opsummere:
Udtrykket \(\delta_j^{(4)}\) kalder man, som nævnt tidligere, også for fejlleddet i den \(j\)’te række i det fjerde lag, og man kan se på ovenstående opdateringsregler, at dette fejlled netop indgår i opdateringen af både vægtene og biasene. Faktisk kan vi, præcis som vi gjorde det tidligere, tillægge dette fejlled en intuitiv god mening. Det kommer vi tilbage til igen senere!
Bemærk, at hvis vi i vores netværk starter med at vælge mere eller mindre tilfældige vægte, så kan vi på baggrund af dem bruge feedforwardligningerne til at udregne, \(a_j^{(4)}\)- og \(a_i^{(3)}\)- værdierne. Samtidig kender vi target-værdierne \(t_j\), og vi kan derfor også udregne fejlleddene \(\delta_j^{(4)}\). Vi har altså alt, hvad vi skal bruge for at benytte ovenstående opdateringsregler.
Opdateringsregler for lag \(3\)
Vi bevæger os nu et trin længere bagud i netværket og udleder opdateringsreglerne for det næstsidste lag - lag \(3\). Altså skal vi have bestemt \[ \frac{\partial E}{\partial w_{ji}^{(3)}} \quad \text{og} \quad \frac{\partial E}{\partial b_j^{(3)}}, \] for \(j \in \{1, 2\}\), \(i \in \{1, 2, 3\}\). Vi må igen se på, hvordan \(w_{ji}^{(3)}\) påvirker tabsfunktionen \(E\). Ser vi på figur figur 1, kan vi se, at \(w_{ji}^{(3)}\) direkte påvirker \(z_j^{(3)}\), som igen direkte påvirker \(a_j^{(3)}\). Nu vil den \(j\)’te neuron i det tredje lag fyre værdien \(a_j^{(3)}\) til alle neuroner i det fjerde lag. Altså vil \(a_j^{(3)}\) påvirke \(z_1^{(4)}, z_2^{(4)}\) og \(z_3^{(4)}\), som bruges til beregning af \(a_1^{(4)}, a_2^{(4)}\) og \(a_3^{(4)}\), som så igen vil påvirke tabsfunktionen \(E\). Det kan illustreres på denne måde \[ \begin{matrix} & & & & z_1^{(4)} \rightarrow a_1^{(4)} & & \\ & & & \nearrow & & \searrow & \\ w_{ji}^{(3)} & \rightarrow & z_j^{(3)} \rightarrow a_j^{(3)} & \rightarrow & z_2^{(4)} \rightarrow a_2^{(4)} & \rightarrow & E \\ & & & \searrow & & \nearrow & \\ & & & & z_3^{(4)} \rightarrow a_3^{(4)} & & \\ \end{matrix} \] I første omgang kan vi skrive \[ \frac{\partial E}{\partial w_{ji}^{(3)}} = \frac{\partial E}{\partial z_j^{(3)}} \cdot \frac{\partial z_j^{(3)}}{\partial w_{ji}^{(3)}} \tag{9}\] og så gentagne gange bruge kædereglen til at udfolde dette udtryk.
Lad os starte med det nemmeste, nemlig \(\frac{\partial z_j^{(3)}}{\partial w_{ji}^{(3)}}\). Ser vi på definitionen af \(z_j^{(3)}\) i (1), kan vi argumentere helt tilsvarende, som da vi ovenfor udledte udtrykket i (7) og får \[ \frac{\partial z_j^{(3)}}{\partial w_{ji}^{(3)}} = a_i^{(2)} \]
Lad os nu kaste os over den første faktor i (9). Vi kan starte med at udnytte denne lidt overordnede måde, som \(z_j^{(3)}\) påvirker \(E\) på \[ z_j^{(3)} \rightarrow a_j^{(3)} \rightarrow E \] Kædereglen giver os derfor i første omgang \[ \frac{\partial E}{\partial z_j^{(3)}} = \frac{\partial E}{\partial a_j^{(3)}} \cdot \frac{\partial a_j^{(3)}}{\partial z_j^{(3)}} \tag{10}\] Igen er sidste faktor nem nok, idet \[ a_j^{(3)} = \sigma (z_j^{(3)}) \] og derfor er \[ \frac{\partial a_j^{(3)}}{\partial z_j^{(3)}} = \sigma' (z_j^{(3)})=\sigma(z_j^{(3)})\cdot (1-\sigma(z_j^{(3)}))= a_j^{(3)} \cdot (1-a_j^{(3)}), \] hvor vi endnu en gang har benyttet, at \(\sigma'(x)=\sigma(x)(1-\sigma(x))\).
Når vi skal bestemme \(\frac{\partial E}{\partial a_j^{(3)}}\) kommer vi ikke udenom kædereglen for funktioner af flere variable. Det bliver tydeligt, når vi zoomer ind på hvordan \(a_j^{(3)}\) påvirker \(E\): \[ \begin{matrix} & & z_1^{(4)} \rightarrow a_1^{(4)} & & \\ & \nearrow & & \searrow & \\ a_j^{(3)} & \rightarrow & z_2^{(4)} \rightarrow a_2^{(4)} & \rightarrow & E \\ & \searrow & & \nearrow & \\ & & z_3^{(4)} \rightarrow a_3^{(4)} & & \\ \end{matrix} \] For at vi senere kan udnytte nogle af de ligninger, som vi udledte i lag \(4\), vil vi faktisk bare nøjes med at se på det, på denne måde: \[ \begin{matrix} & & z_1^{(4)} & & \\ & \nearrow & & \searrow & \\ a_j^{(3)} & \rightarrow & z_2^{(4)} & \rightarrow & E \\ & \searrow & & \nearrow & \\ & & z_3^{(4)} & & \\ \end{matrix} \] Nu er vi endelig klar til at bruge kædereglen for funktioner af flere variable: \[\begin{align} \frac{\partial E}{\partial a_j^{(3)}} &= \frac{\partial E}{\partial z_1^{(4)}} \cdot \frac{\partial z_1^{(4)}}{\partial a_j^{(3)}} + \frac{\partial E}{\partial z_2^{(4)}} \cdot \frac{\partial z_2^{(4)}}{\partial a_j^{(3)}} + \frac{\partial E}{\partial z_3^{(4)}} \cdot \frac{\partial z_3^{(4)}}{\partial a_j^{(3)}} \\ &= \sum_{k=1}^{3}\frac{\partial E}{\partial z_k^{(4)}} \cdot \frac{\partial z_k^{(4)}}{\partial a_j^{(3)}} \end{align}\] Se nu dukker der noget op, som vi har set før! Nemlig det fejlled, som vi definerede i (8), og som vi allerede har regnet ud, da vi opdaterede vægtene og biasene i lag \(4\). Tænk lige over det - det er faktisk ret fedt! Dvs. at vi kan skrive: \[ \begin{aligned} \frac{\partial E}{\partial a_j^{(3)}} &= \sum_{k=1}^{3} \delta_k^{(4)} \cdot \frac{\partial z_k^{(4)}}{\partial a_j^{(3)}} \end{aligned} \tag{11}\] Så mangler vi kun lige at finde \(\frac{\partial z_k^{(4)}}{\partial a_j^{(3)}}\)! Fra (2) har vi, at \[ z_k^{(4)} = \sum_i w_{ki}^{(4)} a_i^{(3)}+b_k^{(4)} \] så \[ \frac{\partial z_k^{(4)}}{\partial a_j^{(3)}} = \frac{\partial}{\partial a_j^{(3)}} \left(\sum_i w_{ki}^{(4)} a_i^{(3)}+b_k^{(4)} \right) \] Når vi skal differentierer summen i ovenstående udtryk, får vi kun et led med, når \(i=j\), fordi i alle andre tilfælde, vil vi med hensyn til \(a_j^{(3)}\) skulle differentiere en konstant. Og da \[ \frac{\partial}{\partial a_j^{(3)}}\left ( w_{kj}^{(4)} a_j^{(3)} \right) = w_{kj}^{(4)} \] har vi altså, at \[ \frac{\partial z_k^{(4)}}{\partial a_j^{(3)}} = w_{kj}^{(4)} \] Indsætter vi dette i (11), har vi nu \[\begin{align} \frac{\partial E}{\partial a_j^{(3)}} = \sum_{k=1}^{3} \delta_k^{(4)} \cdot \frac{\partial z_k^{(4)}}{\partial a_j^{(3)}} = \sum_{k=1}^{3} \delta_k^{(4)} \cdot w_{kj}^{(4)} \end{align}\]
Nu skal vi i første omgang tilbage til (10) og indsætte det vi netop er kommet frem til: \[\begin{align} \frac{\partial E}{\partial z_j^{(3)}}=\underbrace{\left ( \sum_{k=1}^{3} \delta_k^{(4)} \cdot w_{kj}^{(4)}\right )}_{\frac{\partial E}{\partial a_j^{(3)}}} \cdot \underbrace{a_j^{(3)} \cdot (1-a_j^{(3)})}_{\frac{\partial a_j^{(3)}}{\partial z_j^{(3)}}} \end{align}\] Som vi gjorde i afsnit 1.2.1, vil vi også give dette lidt lange udtryk en særlig betegnelse, nemlig \[\begin{align} \delta_j^{(3)} = \frac{\partial E}{\partial z_j^{(3)}}=\left ( \sum_{k=1}^{3} \delta_k^{(4)} \cdot w_{kj}^{(4)}\right ) \cdot a_j^{(3)} \cdot (1-a_j^{(3)}) \end{align}\] Det kan vist godt være lidt svært at bevare overblikket her, men nu er vi faktisk i mål! Vi indsætter i (9) \[\begin{align} \frac{\partial E}{\partial w_{ji}^{(3)}} &= \frac{\partial E}{\partial z_j^{(3)}} \cdot \frac{\partial z_j^{(3)}}{\partial w_{ji}^{(3)}} \\ &= \delta_j^{(3)} \cdot a_i^{(2)} \end{align}\]
Det er nu en smal sag at bestemme \(\frac{\partial E}{\partial b_j^{(3)}}\), da \[\begin{align} \frac{\partial E}{\partial b_j^{(3)}} &= \frac{\partial E}{\partial z_j^{(3)}} \cdot \frac{\partial z_j^{(3)}}{\partial b_j^{(3)}} \\ &= \delta_j^{(3)}\cdot \frac{\partial z_j^{(3)}}{\partial b_j^{(3)}} \end{align}\] Fra (1) har vi, at \[ z_j^{(3)} = \sum_{i=1}^3 w_{ji}^{(3)} a_i^{(2)} + b_j^{(3)} \] og derfor er \[ \frac{\partial z_j^{(3)}}{\partial b_j^{(3)}} = 1 \] Altså får vi \[\begin{align} \frac{\partial E}{\partial b_j^{(3)}} = \delta_j^{(3)} \end{align}\] Glæden er stor, da vi nu har alle ingredienser til at opskrive opdateringsreglerne for det tredje lag!
Bemærk, at udgangspunktet for ovenstående er, at vi først har lavet et feedforward i netværket, så vi har alle \(a_i^{(2)}\)- og \(a_j^{(3)}\)-værdier. Derudover har vi allerede opdateret vægtene og biasene i lag \(4\). Derfor kender vi også fejleddene \(\delta_k^{(4)}\) fra lag \(4\), som indgår i beregningen af \(\delta_j^{(3)}\) i (12). Altså er det muligt at foretage de beregninger, som opdateringsreglerne i lag \(3\) kræver.
Opdateringsregler for lag \(2\)
Vi er nu fremme ved det sidste lag, hvor vi skal have opdateret vægte og bias (husk på at \(a_i^{(1)}\)-værdierne jo ikke skal beregnes, men er inputværdierne til netværket). Den gode nyhed her er, at der absolut intet nyt er under solen! Vi vil derfor heller ikke gå i drabelige deltaljer med alle udregninger her, men blot skitsere idéen.
Vi er nu på jagt efter \[ \frac{\partial E}{\partial w_{ji}^{(2)}} \quad \text{og} \quad \frac{\partial E}{\partial b_j^{(2)}} \] og kigger vi på vores netværk i figur 1 kan vi se følgende afhængigheder: \[ \begin{matrix} & & & & z_1^{(3)} & & \\ & & & \nearrow & & \searrow & \\ w_{ji}^{(2)} & \rightarrow & z_j^{(2)} \rightarrow a_j^{(2)} & & & & E \\ & & & \searrow & & \nearrow & \\ & & & & z_2^{(3)} & & \\ \end{matrix} \] Vi kan nu igen skrive \[ \frac{\partial E}{\partial w_{ji}^{(2)}} = \frac{\partial E}{\partial z_j^{(2)}} \cdot \frac{\partial z_j^{(2)}}{\partial w_{ji}^{(2)}} \tag{13}\] Helt analogt til tidligere ses det nemt, at \[ \frac{\partial z_j^{(2)}}{\partial w_{ji}^{(2)}} = a_i^{(1)} \] og kædreglen giver igen, at \[ \frac{\partial E}{\partial z_j^{(2)}}= \frac{\partial E}{\partial a_j^{(2)}} \cdot \frac{\partial a_j^{(2)}}{\partial z_j^{(2)}} \tag{14}\] Her fås også uden problemer, at den sidste faktor kan skrives som \[ \frac{\partial a_j^{(2)}}{\partial z_j^{(2)}} = a_j^{(2)} \cdot (1-a_j^{(2)}) \] og bruger man kædereglen for funktioner af flere variable, kommer man frem til, at \[\begin{align} \frac{\partial E}{\partial a_j^{(2)}} &= \sum_{k=1}^2 \frac{\partial E}{\partial z_k^{(3)}} \cdot \frac{\partial z_k^{(3)}}{\partial a_j^{(2)}} \\ &= \sum_{k=1}^2 \delta_k^{(3)} w_{kj}^{(3)}, \end{align}\] hvor vi allerede har udregnet \(\delta_k^{(3)}\), da vi opdaterede vægtene og biasene i lag \(3\).
Indsætter vi i (14) og samtidig definerer fejlleddet \(\delta_j^{(2)}\) for det andet lag, får vi \[ \delta_j^{(2)} = \frac{\partial E}{\partial z_j^{(2)}} = \left ( \sum_{k=1}^2 \delta_k^{(3)} w_{kj}^{(3)} \right ) \cdot a_j^{(2)} \cdot (1-a_j^{(2)}) \] Alt i alt ender vi med \[\begin{align} \frac{\partial E}{\partial w_{ji}^{(2)}} &= \delta_j^{(2)} \cdot a_i^{(1)} \\ &= \delta_j^{(2)} \cdot x_i \end{align}\] fordi alle \(a_i^{(1)}\)-værdierne svarer til selve inputværdierne \(x_i\) til netværket.
Det er nu ikke svært at se, at \[ \frac{\partial E}{\partial b_j^{(2)}} = \delta_j^{(2)} \] og vi får derfor følgende opdateringsregler for lag 2:
Var det så egentlig smart med alle de indekser?
Hvis man er nået hertil, kan man godt følge sig en lille smule forpustet. Der har godt nok været mange indekser at holde styr på! Både nogle der var sænkede, og nogle der var hævede og sat i parenteser! Alligevel kan man måske godt se fidusen nu.
Hvis vi ser på de opdateringsregler, som vi lige har udledt, så kan man se, at selve opdateringsreglerne af vægte og bias følger præcis samme form. Faktisk kan man, hvis man sammenligner opdateringsreglerne for de tre lag se, at opdateringsreglerne er på denne form:
Bemærk her, at da vi allerede har lavet en feedforward i netværket, så kender vi outputværdierne \(a_i^{(\text{lag})}\) i alle lag. Det vil sige, at vi kan opdatere vægtene og biasene, når blot vi kan beregne fejlleddene.
Den eneste reelle forskel på opdateringsreglerne er, at fejlleddene udregnes lidt forskelligt, alt efter om der er tale om outputlaget eller et skjult lag:
Bemærk her, at fejlleddene fra outputlaget uden videre kan beregnes, da vi kender target-værdierne \(t_j\) og outputværdierne \(y_j\) fra netværket (fordi vi allerede har lavet en feedforward). Vi kan også beregne fejlleddene i alle skjulte lag, idet vi hele tiden arbejder bagud i netværket (backpropagation). Det vil sige, at vi hele tiden har adgang til fejlleddene i laget længere fremme (lag+1), hvor (lag+1) første gang vil svare til outputlaget. Desuden kender vi pga. feedforward alle outputværdier \(a_j^{(\text{(lag)})}\) og alle vægte \(w_{kj}^{(\text{(lag+1)})}\). Derfor kan vi også beregne fejlleddene i alle de skjulte lag.
Denne indsigt og den generelle overordnede struktur på opdateringsreglerne, var meget svær at indse med fremgangsmåde i afsnittet Hvordan træner man et kunstigt neuralt netværk?. Her druknede alt bare i et sandt bogstavshelvede!
Der er et par andre interessante ting at sige om beregningen af fejlleddene. Lad os først se på outputlaget: \[ \delta_j^{(\text{outputlag})} = -(t_j-y_j) \cdot y_j \cdot (1-y_j) \] Hvis der er stor forskel på target-værdien \(t_j\) og outputværdien \(y_j\), så bliver forskellen \(t_j-y_j\) numerisk stor. Altså vil en stor forskel på det, vi ønsker, og det vi får ud af netværket betyde, at fejlleddet bliver større og i sidste ende, at de vægte, som direkte påvirker outputtet, også vil blive opdateret meget. Endelig ser vi igen, at hvis outputneuronen er mættet (dvs. at \(y_j\) enten er tæt på \(0\) eller \(1\)), så vil fejlleddet ikke blive opdateret i samme grad, som hvis outputneuronen ikke havde været mættet (fordi hvis \(y_j\) enten er tæt på \(0\) eller \(1\), så vil \(y_j \cdot (1-y_j)\) være tæt på \(0\)).
Vi ser altså, at fejlleddet fra det sidste lag direkte afhænger af hvor stor forskellen er på target-værdi og outputværdi.
Ser vi så på fejlleddene fra de skjulte lag: \[ \delta_j^{(\text{lag})} = \left ( \sum_{k} \delta_k^{(\text{lag+1})} w_{kj}^{(\text{lag+1})} \right ) \cdot a_j^{(\text{lag})} \cdot (1-a_j^{(\text{lag})}) \] Så kan vi igen se, at hvis den tilhørende outputneuron, som fyrer værdien \(a_j^{(\text{lag})}\), er mættet, så vil fejlleddet være tættere på \(0\), end hvis neuronen ikke havde været mættet. Samtidig kan vi også se, at der i fejlleddet indgår en vægtet sum af alle fejlleddene fra laget længere fremme: \[ \sum_{k} \delta_k^{(\text{lag+1})} w_{kj}^{(\text{lag+1})} \] På den måde vil store fejl i laget længere fremme også få indflydelse på fejlleddet i det nuværende lag.
Kunstige neurale netværk helt generelt
Med det benarbejde vi lige har været igennem, ligger det faktisk lige til højrebenet at generalisere overstående til et vilkårligt kunstigt neuralt netværk.
Vi forestiller os nu, at vi har \(K\) lag i netværket, som det er illustreret på figur 4.
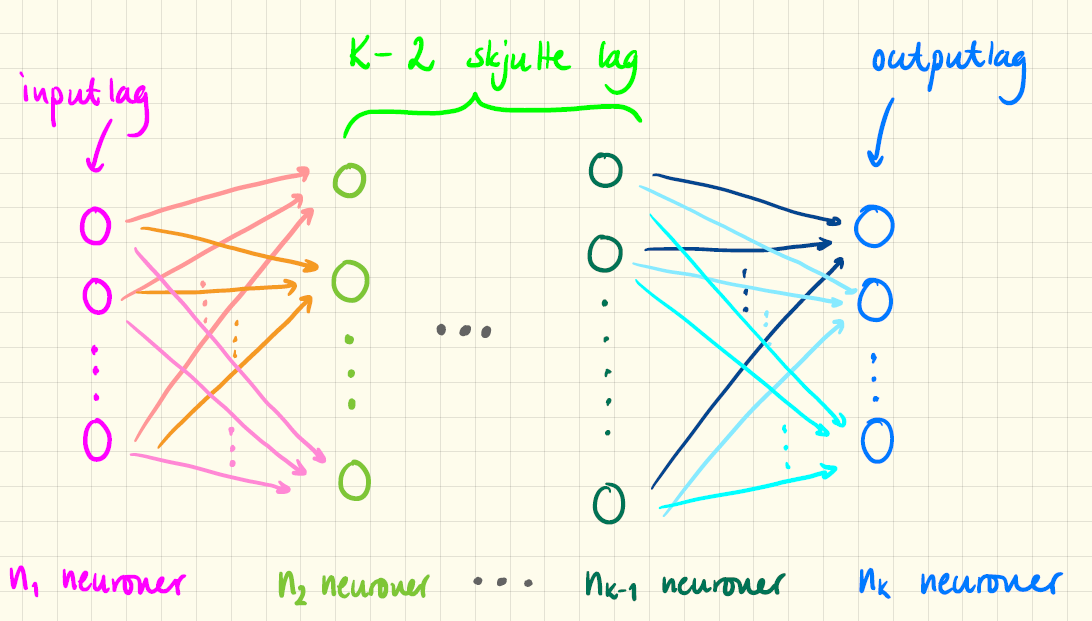
Det vil sige ét inputlag, ét outputlag og \(K-2\) skjulte lag. Antallet af neuroner i hvert lag kan variere og behøver ikke at være det samme. Så lad os navngive antallet af neuroner i de \(K\) lag på denne måde: \[ n_1, n_2, \dots, n_k, \dots, n_K \] Inputværdierne til netværket betegner vi: \[ a_1^{(1)}, a_2^{(1)}, \dots, a_{n_1}^{(1)} \] Feedforward ligningerne er nu helt identiske med dem vi opstillede i afsnit 1.1:
Hvis vi også kalder outputværdierne fra netværket for \[ y_1, y_2, \dots, y_{n_K} \] så beregnes disse værdier altså ved \[\begin{align} y_j = a_j^{(K)} &= \sigma(z_j^{(K)}) \end{align}\] for \(j \in \{1, 2, \dots, n_K \}\).
Backpropagation - generelt
Lad os så se på backpropagation. Vi ved fra det foregående, at der reelt set kun er to ting, vi skal gøre:
Finde opdateringsreglerne for vægte og bias i outputlaget.
Finde opdateringsreglerne for vægte og bias i et vilkårligt skjult lag.
Opdateringsregler i outputlaget
Vores tabsfunktion er stadig \[ E= \frac{1}{2} \sum_{i=1}^{n_K} \left ( t_i - a_i^{(K)} \right )^2, \] hvor \(t_i\) igen er targetværdierne. Vi skal bestemme \[ \frac{\partial E}{\partial w_{ji}^{(K)}} \quad \text{og} \quad \frac{\partial E}{\partial b_j^{(K)}} \] Vi gør præcis som i afsnit 1.2.1. Vi indser først, at vi har denne direkte afhængighed fra \(w_{ji}^{(K)}\) til \(E\): \[ w_{ji}^{(K)} \rightarrow z_j^{(K)} \rightarrow a_j^{(K)} \rightarrow E \] Derfor får vi \[ \frac{\partial E}{\partial w_{ji}^{(K)}} = \frac{\partial E}{\partial z_j^{(K)}} \cdot \frac{\partial z_j^{(K)}}{\partial w_{ji}^{(K)}} \tag{18}\] På grund af feedforwardligningen i (16) får vi for det første, at \[ \frac{\partial z_j^{(K)}}{\partial w_{ji}^{(K)}} = a_i^{(K-1)} \tag{19}\] Nu bruger vi kædereglen til at bestemme \[ \frac{\partial E}{\partial z_j^{(K)}} = \frac{\partial E}{\partial a_j^{(K)}} \cdot \frac{\partial a_j^{(K)}}{\partial z_j^{(K)}} \tag{20}\] På grund af feedforwardligningen i (17) og egenskaben ved differentialkvotienten af sigmoid-funktionen får vi sidste faktor til \[ \frac{\partial a_j^{(K)}}{\partial z_j^{(K)}} = a_j^{(K)}\cdot (1-a_j^{(K)}) \] Endelig får vi, ved at differentiere tabsfunktionen med hensyn til \(a_j^{(K)}\) \[ \frac{\partial E}{\partial a_j^{(K)}} = -(t_j-a_j^{(K)}) \] Vi definerer nu igen fejlleddet for outputlaget \(\delta_j^{(K)}\), som tidligere \[ \delta_j^{(K)} = \frac{\partial E}{\partial z_j^{(K)}} \] og indsætter vi det, vi netop har udledt, i (20) får vi \[ \delta_j^{(K)} = -(t_j-a_j^{(K)}) \cdot a_j^{(K)} \cdot (1-a_j^{(K)}) \] Indsætter vi nu det hele i (18), har vi altså: \[ \frac{\partial E}{\partial w_{ji}^{(K)}} = \delta_j^{(K)} \cdot a_i^{(K-1)} \] Det er ikke svært at overbevise sig selv om, at \[ \frac{\partial E}{\partial b_j^{(K)}} = \delta_j^{(K)} \] og derfor har vi:
Opdateringsregler i et vilkårligt skjult lag
Vi ser nu på et vilkårligt skjult lag \(k\), som hverken er inputlaget eller outputlaget. Det vil sige, at \(k \in \{2, 3, \dots, K-1 \}\). Vi antager, at vi har kørt backpropagation på alle lag, der ligger længere fremme i netværket, og specielt har vi altså beregnet fejlleddene i lag \(k+1:\) \[ \delta_j^{(k+1)} = \frac{\partial E}{\partial z_j^{(k+1)}} \] Vi indser først, at vi har denne afhængighed fra \(w_{ji}^{(k)}\) til tabsfunktionen \(E\): \[ \begin{matrix} & & & & z_1^{(k+1)} & & \\ & & & \nearrow & \vdots & \searrow & \\ w_{ji}^{(k)} & \rightarrow & z_j^{(k)} \rightarrow a_j^{(k)} & \rightarrow & z_j^{(k+1)} & \rightarrow & E \\ & & & \searrow & \vdots & \nearrow & \\ & & & & z_{n_{k+1}}^{(k+1)} & & \\ \end{matrix} \tag{21}\] Vi starter som tidligere med at bruge kædereglen én gang: \[ \frac{\partial E}{\partial w_{ji}^{(k)}} = \frac{\partial E}{\partial z_j^{(k)}} \cdot \frac{\partial z_j^{(k)}}{\partial w_{ji}^{(k)}} \tag{22}\] Fra feedforwardligningen i (16) får vi for det første, at \[ \frac{\partial z_j^{(k)}}{\partial w_{ji}^{(k)}} = a_i^{(k-1)} \] Endnu en anvendelse af kædereglen, og hvor vi også i samme hug definerer fejlleddet \(\delta_j^{(k)}\) for det \(k\)’te skjulte lag, giver: \[ \delta_j^{(k)} = \frac{\partial E}{\partial z_j^{(k)}}= \frac{\partial E}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} \tag{23}\] Den sidste partielle afledede kan vi udlede fra feedforwardligningen (17) og egenskaben ved differentialkvotienten af sigmoid-funktionen: \[ \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} = a_j^{(k)} \cdot (1-a_j^{(k)}) \] For at beregne \(\frac{\partial E}{\partial a_j^{(k)}}\) må vi have fat i kædereglen for funktioner af flere variable (se illustrationen i (21): \[\begin{align} \frac{\partial E}{\partial a_j^{(k)}} = \sum_{i=1}^{n_{k+1}} \frac{\partial E}{\partial z_i^{(k+1)}} \cdot \frac{\partial z_i^{(k+1)}}{\partial a_j^{(k)}} \end{align}\] Vi udnytter nu, at vi allerede kender fejlleddene fra lag \(k+1\) og kan derfor omskrive til
\[ \frac{\partial E}{\partial a_j^{(k)}} = \sum_{i=1}^{n_{k+1}} \delta_i^{(k+1)} \cdot \frac{\partial z_i^{(k+1)}}{\partial a_j^{(k)}} \tag{24}\]
Fra feedforwardligningen i (16) får vi, at \(z_i^{(k+1)}\) kan skrives som \[ z_i^{(k+1)} = \sum_{j} w_{ij}^{(k+1)} a_j^{(k)} + b_i^{(k+1)} \] og derfor er \[\begin{align} \frac{\partial z_i^{(k+1)}}{\partial a_j^{(k)}} = w_{ij}^{(k+1)} \end{align}\] Indsætter vi i (24) fås \[\begin{align} \frac{\partial E}{\partial a_j^{(k)}} = \sum_{i=1}^{n_{k+1}} \delta_i^{(k+1)} \cdot w_{ij}^{(k+1)} \end{align}\] og ved indsættelse i (23) får vi nu fejlleddet i det \(k\)’te lag \[ \delta_j^{(k)} = \frac{\partial E}{\partial z_j^{(k)}}= \left ( \sum_{i=1}^{n_{k+1}} \delta_i^{(k+1)} \cdot w_{ij}^{(k+1)} \right) \cdot a_j^{(k)} \cdot (1-a_j^{(k)}) \] Vi bruger nu udtrykket for \(\frac{\partial E}{\partial w_{ji}^{(k)}}\) i (22) og ender med \[\begin{align} \frac{\partial E}{\partial w_{ji}^{(k)}} = \delta_j^{(k)} \cdot a_i^{(k-1)} \end{align}\] og tilsvarende får vi også, at \[ \frac{\partial E}{\partial b_j^{(k)}} = \delta_j^{(k)} \] Opdateringsreglerne for et vilkårligt skjult lag bliver så:
Stokastisk gradientnedstigning
Vi har faktisk snydt lidt… Okay – indrømmet – det er lidt træls at komme at sige nu! Men i alt hvad vi har lavet indtil nu, har vi kun kigget på ét træningseksempel. Vi har ladet inputværdierne for det ene træningseksempel "kører igennem" netværket (feedforward), beregnet tabsfunktionen og brugt resultatet herfra til at opdatere alle vægtene (backpropagation). Men vi har jo ikke kun ét træningseksempel. Vi har faktisk rigtig mange! Måske ligefrem tusindvis af træningsdata. Men hvad gør man så?
Lad os lige genopfriske den tabsfunktion, som vi endte med i det helt generelle tilfælde: \[ E= \frac{1}{2} \sum_{i=1}^{n_K} \left ( t_i - a_i^{(K)} \right )^2. \tag{25}\] Her er \(t_i\) target-værdien for den \(i\)’te outputneuron for lige præcis det træningseksempel vi står med. Husk på at et givet træningseksempel består af inputværdierne \[ x_1, x_2, \dots, x_{n_1} \] og de ønskede target-værdier \[ t_1, t_2, \dots, t_{n_K}. \] Når vi kører disse inputværdier igennem netværket, får de selvfølgelig i sidste ende direkte betydning for outputværdierne i det sidste lag (\(K\)): \[ a_1^{(K)}, a_2^{(K)}, \cdots, a_{n_K}^{(K)}. \] Det vil sige, at i vores tabsfunktion i (25), så afhænger både \(t_i\)’erne og \(a_i^{(K)}\)’erne af træningseksemplet. Hvis vi sådan lidt generelt benævner vores træningseksempel med \(x\), så vil det kunne udtrykkes sådan her: \[ E_x= \frac{1}{2} \sum_{i=1}^{n_K} \left ( t_{x,i} - a_{x,i}^{(K)} \right )^2, \] hvor så \(t_{x,i}\) er target-værdien for den \(i\)’te outputneuron fra træningsdata \(x\) og \(a_{x,i}^{(K)}\) er outputværdien for den \(i\)’te outputneuron, som er beregnet på baggrund af inputværdierne fra træningsdata \(x\).
Den samlede tabsfunktion, som er den, vi i virkeligheden ønsker at minimere, bliver så gennemsnittet af tabsfunktionerne hørende til de enkelte træningsdata: \[ E = \frac{1}{n} \sum_x E_x= \frac{1}{n} \sum_x \left ( \frac{1}{2} \sum_{i=1}^{n_K} \left ( t_{x,i} - a_{x,i}^{(K)} \right )^2 \right ). \tag{26}\] Husk på at vi er ude efter \[ \frac{\partial E}{\partial w_{ji}^{(k)}} \quad \text{og} \quad \frac{\partial E}{\partial b_j^{(k)}} \] for \(k \in \{2, 3, \dots, K\}\) og hvor \(E\) nu er summen i (26). Heldigvis kan vi differentiere ledvis, og der gælder derfor \[ \frac{\partial E}{\partial w_{ji}^{(k)}} = \frac{1}{n} \sum_x \frac{\partial E_x}{\partial w_{ji}^{(k)}} \] og tilsvarende \[ \frac{\partial E}{\partial b_j^{(k)}} = \frac{1}{n} \sum_x \frac{\partial E_x}{\partial b_j^{(k)}} \] Det kommer så til at betyde, at opdateringsreglerne nu generelt bliver på formen \[ w_{ji}^{(k)} \leftarrow w_{ji}^{(k)}-\eta \cdot \frac{\partial E}{\partial w_{ji}^{(k)}} = w_{ji}^{(k)}-\eta \cdot \frac{1}{n} \sum_x \frac{\partial E_x}{\partial w_{ji}^{(k)}} \tag{27}\] og tilsvarende for biasene \[ b_j^{(k)} \leftarrow b_j^{(k)} -\eta \cdot \frac{\partial E}{\partial b_j^{(k)}} = b_j^{(k)}-\eta \cdot \frac{1}{n} \sum_x \frac{\partial E_x}{\partial b_j^{(k)}} \tag{28}\] Alle leddene \(\frac{\partial E_x}{\partial w_{ji}^{(k)}}\) og \(\frac{\partial E_x}{\partial b_j^{(k)}}\), som indgår i opdateringsreglerne, svarer netop til hvad vi har udledt i de foregående afsnit, fordi vi jo netop her kun så på ét træningseksempel ad gangen. Hvis vi overfører dette til opdateringsreglerne i outputlaget, så vil vi f.eks. få
Og helt tilsvarende vil det se ud for opdateringsreglerne i de skjulte lag.
Lad os lige dvæle lidt ved, hvad det her, det egentlig betyder. Lad os sige at vi har \(1000\) træningsdata. Så skal vi lade de \(1000\) træningsdata kører igennem netværket, så vi kan beregne de \(1000\) led, som indgår i de ovenstående summer. Herefter kan vi opdatere alle vægte og bias én gang. Det vil blot være ét lille skridt på vej ned i dalen mod det lokale minimum, som vi er på jagt efter. Dette lille skridt skal gentages rigtig mange gange, indtil værdien af tabsfunktionen ser ud til at begynde at konvergere – svarende til at vi har ramt det lokale minimum.
Så selvom gradientnedstigning kan bruges til at finde et lokalt minimum for tabsfunktionen \(E\), så er det faktisk også en beregningsmæssig stor og tung opgave! Derfor er der forsket meget videre i at gøre det endnu bedre og endnu hurtigere. I algoritmer som disse er der ofte et trade-off: Man kan gøre noget hurtigere ved at bruge mere hukommelse – eller bruge mindre hukommelse ved at gøre det en smule langsommere. En af de teknikker, der er kommet ud af den forskning, er, at man kan bruge mindre hukommelse ved i hvert opdateringsskridt kun at bruge en tilfældigt udvalgt del af træningsdata – det kunne f.eks. være \(10\%\) af alle træningsdata. Så vil man i hvert skridt stadig bruge opdateringsreglerne i (27) og (28), men hvor der nu kun summeres over de \(10 \%\) af træningsdatene. Hver gang man laver et nyt opdateringsskridt, vil man tage en ny tilfældigt udvalgt del af træningsdata. Denne teknik kalder man stokastisk gradientnedstigning (stochastic gradient descent). Og der er endnu flere af sådanne små ændringer, der enten gør algoritmen hurtigere eller, at den bruger mindre hukommelse. Det vil komme an på den enkelte anvendelse, hvad der er vigtigst her.