Hvorfor er simple neurale netværk smartere end ADALINE?
I noten om perceptroner beskrev vi perceptron learning algoritmen, som altid konvergerer, hvis data er lineært separabel. Men verden er sjældent lineært separabel, og derfor introducerede vi ADALINE algoritmen, som også virker, selvom data ikke er lineært separabel. I noten om simple neurale netværk beskrev vi en helt tredje metode.
Vi vil her med et enkelt lille eksempel afsløre, at ADALINE ikke altid er så smart, som man kunne tro. Dernæst vil vi forklare hvordan simple neurale netværk, kan være en løsning på det skitserede problem.
Vi vil se på data i nedenstående tabel
| \(x_1\) | \(x_2\) | Targetværdi |
|---|---|---|
| \(-0.5\) | \(0.5\) | \(1\) |
| \(-0.3\) | \(0.3\) | \(1\) |
| \(-0.1\) | \(0.7\) | \(1\) |
| \(0.1\) | \(0.4\) | \(-1\) |
| \(-0.1\) | \(0.2\) | \(-1\) |
| \(0.1\) | \(-0.1\) | \(-1\) |
Bemærk, at i ADALINE er targetværdien \(t \in \{-1,1\}\).
I figur 1 har vi indtegnet punkterne \((x_1,x_2)\) og farvet punkterne med en targetværdi på \(1\) blå og dem med en targetværdi på \(-1\) røde.
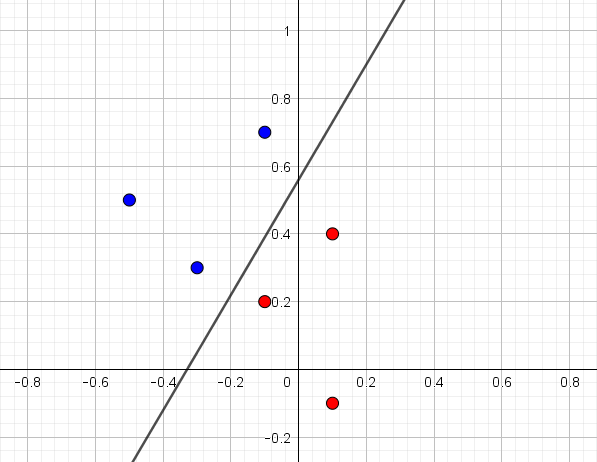
Det er tydeligt, at punkterne er lineært separable og den indtegnede linje er også den som ADALINE giver1. Du kan selv prøve ADALINE her. De estimerede vægte er \(w_0=-0.9346, w_1=-2.838\) og \(w_2=1.668\).Det vil sige, at den indtegnede linje har ligning
1 Her er alle startvægte sat til \(0\), learning rate er på \(0.1\), stop-kriterie er på \(0.000001\) og maksimalt antal iterationer er sat til \(50000\).
\[ -0.9346-2.838 x_1 + 1.668x_2=0 \]
Det er alt sammen meget fint, men lad os nu prøve at indtegne et nyt rødt punkt:
| \(x_1\) | \(x_2\) | Targetværdi |
|---|---|---|
| \(1\) | \(-1\) | \(-1\) |
Det nye punkt er indtegnet i figur 2 sammen med de øvrige seks punkter. Det er tydeligt, at data stadig er lineært separabel.
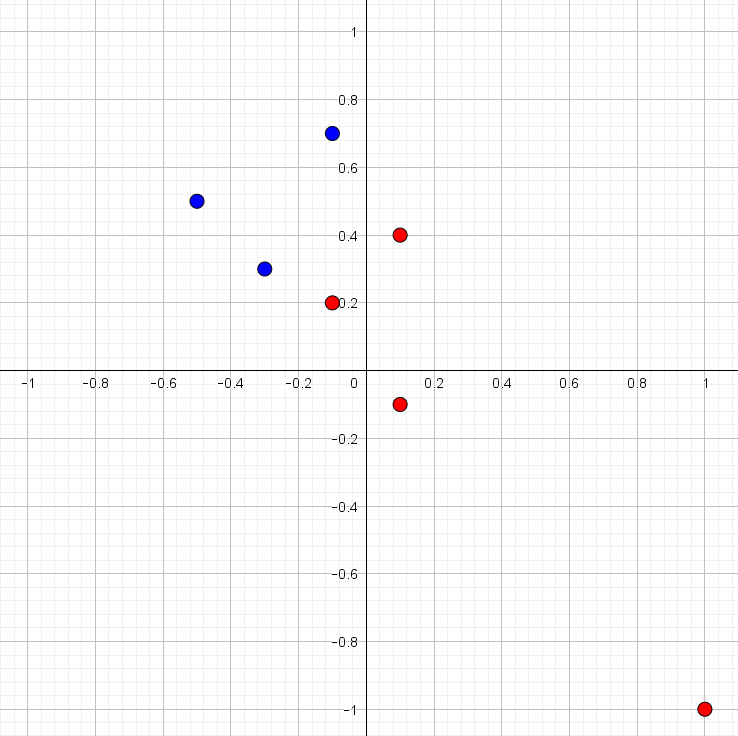
Hvis vi prøver at køre ADALINE algoritmen fås linjen, som er indtegnet i figur 3. Vi kan allerede se nu, at det er helt skørt. Data er lineært separabel, men alligevel er der et rødt punkt, som bliver klassificeret forkert – faktisk var den oprindelige linje fra figur 1 bedre.
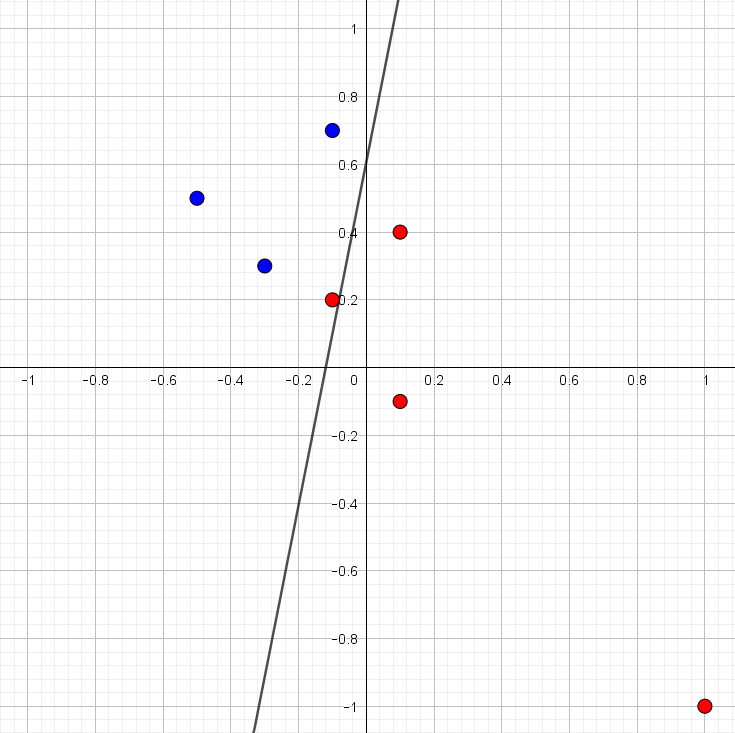
Det er jo ikke ligefrem super overbevisende. Data er lineært separabel og alligevel kan ADALINE ikke finde ud af at finde en ret linje, som kan adskille de røde punkter fra de blå!
Hvis vi skal forstå, hvad der sker, må vi se lidt nærmere på den tabsfunktion, som ADALINE forsøger at mininere. Fra afsnittet om ADALINE ved vi, at tabsfunktionen2 er
2 Bemærk her, at det ikke er afgørende, at der er ganget med \(1/2\) – det viser sig bare smartere senere.
\[ \begin{aligned} E(w_0, w_1, &\dots, w_n)\\ &= \frac{1}{2} \sum_{m=1}^{M} \left (t_m- (w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}) \right)^2 \end{aligned} \tag{1}\]
hvor det \(m\)’te træningseksempel er \[(x_{m,1}, x_{m,2}, \dots, x_{m,n}, t_m)\]
Det vil sige, at det \(m\)’te træningseksempel giver et bidrag til tabsfunktionen på
\[ \left ( t_m- (w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}) \right)^2 \]
For et blåt punkt med \(t_m=1\) vil det sige, at bidraget til tabsfunktionen er præcis \(0,\) hvis \[ 1- (w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n})=0 \] og for et rødt punkt med \(t_m=-1\) er bidraget til tabsfunktionen præcis \(0,\) hvis \[ -1- (w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n})=0 \] Nu er \(1- (w_0 + w_1 \cdot x_1 + \cdots + w_n \cdot x_n)=0\) og \(-1- (w_0 + w_1 \cdot x_1 + \cdots + w_n \cdot x_n)=0\) jo bare ligninger for rette linjer3. Disse linjer ses indtegnet på figur 4 (som henholdsvis en blå og rød stiplet linje) sammen med de oprindelige seks punkter og den linje, som ADALINE fandt baseret på disse seks punkter. Samtidig er det for hvert punkt markeret, hvor meget dette punkt bidrager til tabsfunktionen.
3 Det er i hvert tilfælde "bare linjer", når \(n=2\). Hvis \(n=3\), er der tale om ligningen for en plan, og hvis \(n>3\), kalder man det for ligningen for en "hyperplan". Men sidstnævnte er visuelt svære at forestille sig, fordi koordinatsystemet, disse hyperplaner skal tegnes i, har en dimension større end \(3\). Og de er ikke så nemme at tegne!
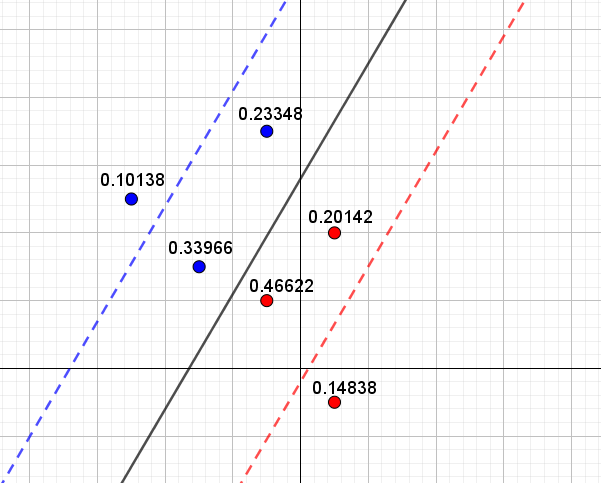
Det ses nu på figur 4, at blå punkter, som ligger tæt på den blå stiplede linje, bidrager mindst til tabsfunktionen, mens røde punkter, som ligger tæt på den røde stiplede linje, ligeledes bidrager mindst til tabsfunktionen. Den samlede værdi af tabsfunktionen4 er her \(0.75\).
4 Værdien udregnes ved at lægge alle bidragene sammen og gange med \(\frac{1}{2}\). Jævnfør udtrykket for tabsfunktionen i (1).
Laver vi nu samme øvelse med det ekstra punkt fås resultat i figur 5.
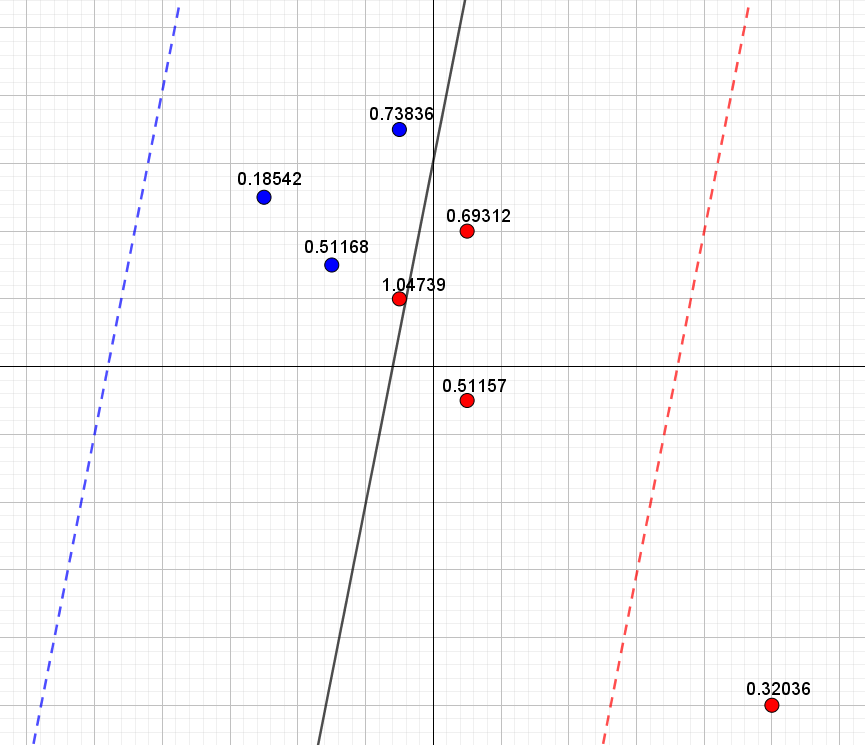
Igen ser vi, at blå punkter tæt på den blå stiplede linje bidrager mindst til tabsfunktionen og tilsvarende for de røde punkter, som ligger tæt på den røde stiplede linje. Det nye punkts bidrag til tabsfunktionen bliver derfor her det mindste bidrag blandt alle de røde punkter. Den samlede værdi af tabsfunktionen er her \(2.00\).
Hvis vi i stedet prøver at bruge vores egen oprindelige linje (baseret på de seks første punkter), som rent faktisk kunne adskille de blå punkter fra de røde, så fås det resultat, som ses i figur 6.
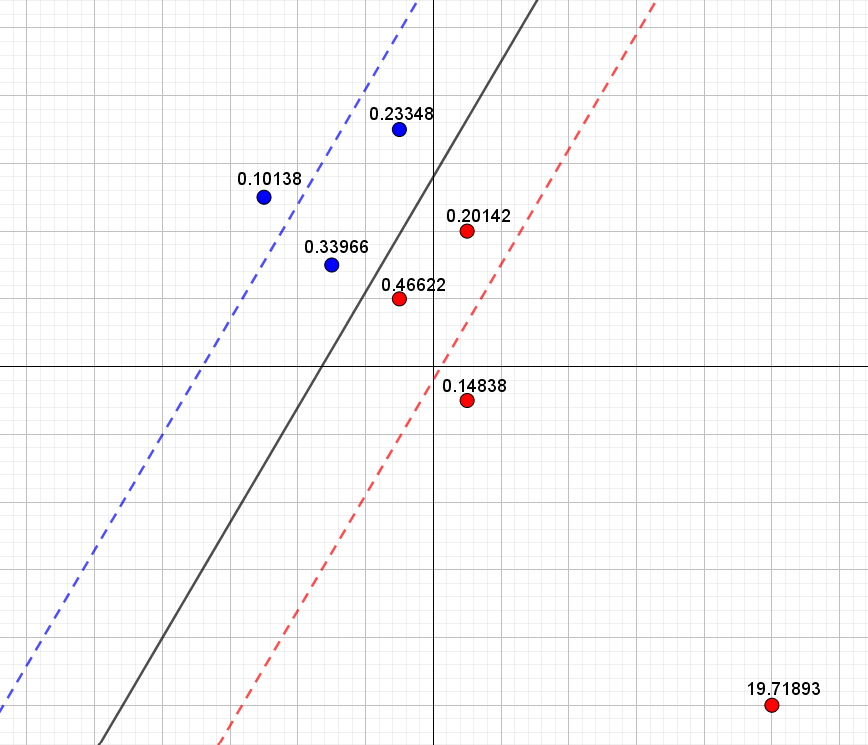
Det er nu tydeligt, at det nye røde punkter ligger så langt væk fra den stiplede røde linje, at det bidrager betydeligt til tabsfunktionen. Derfor er den samlede værdi af tabsfunktionen \(10.60\) – og derfor vælger ADALINE linjen i figur 5 til at adskille punkterne. Ikke fordi, det er den linje, som giver den laveste andel af korrekt klassificerede, men fordi det er den linje, som minimerer tabsfunktionen! Det kan jo godt virke lidt skørt, når vi selv kan indtegne en linje, som kan separere alle punkterne.
Simple neurale netværk og aktiveringsfunktioner
Problemet med ADALINE, som vi har set i eksemplet ovenfor, opstår fordi, et ekstremt punkt får lov til at "trække" uforholdsmæssigt meget i den linje, som ADALINE finder, for at dette punkts bidrag til tabsfunktionen ikke skal blive alt for stort.
Vi så det i figur 5 og figur 6. I figur 5 brugte vi den linje, som ADALINE gav, og her var det ekstreme punkts bidrag til tabsfunktionen på \(0.32\). I figur 6 valgte vi en linje, som oplagt er bedre til at adskille de blå punkter fra de røde, men her er det ekstreme punkts bidrag til tabsfunktionen helt oppe på \(19.72\).
For at forstå det lidt bedre skal vi måske lige repetere, hvordan man finder afstanden fra et punkt \(P(x_1,y_1)\) til en linje \(l\) med ligning \(ax+by+c=0\):
\[ \textrm{dist}(P,l)=\frac{|a x_1 + b y_1 +c|}{\sqrt{a^2+b^2}} \]
Denne afstandsformel kan generaliseres, så afstanden fra et punkt \(P(x_{m,1}, x_{m,2}, \dots, x_{m,n})\) (i et \(n\)-dimensionalt rum!) til planen \(\alpha\) med ligning \(w_0+w_1 x_1 + w_2 x_2 + \cdots + w_n x_n=0\) er:
\[ \textrm{dist}(P,\alpha)=\frac{|w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}|}{\sqrt{w_1^2 + w_2^2 + \cdots + w_n^2}} \]
Det vil sige, at udtrykket i tælleren \(|w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}|\) bliver et mål for hvor langt væk punktet \(P(x_{m,1}, x_{m,2}, \dots, x_{m,n})\) ligger fra planen. Det forklarer, hvordan et ekstremt punkt kan give et meget stort bidrag til tabsfunktionen:
\[ \left ( t- (w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}) \right)^2 \tag{2}\]
Hvis punktet ligger langt væk fra den plan, som måske umiddelbart ser fornuftig ud, så vil punktet give et stort bidrag til tabsfunktionen, fordi værdien af \(w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}\) bliver stor, og dermed vil bidraget til tabsfunktionen i (2) også blive stort!
Alt det her leder os frem til, at valget af tabsfunktion måske i virkeligheden ikke er super smart. Problemet opstår grundlæggende, fordi targetværdien \(t\) og udtrykket i den inderste parentes i (2) er på to helt vidt forskellige skalaer. Targetværdien er enten \(-1\) eller \(1\), mens udtrykket \(w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}\) kan antage en hvilken som helst reel værdi – en værdi som kan blive vældig stor, hvis punktet \(P(x_{m,1}, x_{m,2}, \dots, x_{m,n})\) ligger langt væk fra planen. Derfor bliver ADALINE nødt til at tvinge planen med ligningen
\[ w_0 + w_1 \cdot x_{1} + \cdots + w_n \cdot x_{n}=0 \]
over mod et ekstremt punkt, sådan at dette punkts bidrag til tabsfunktionen ikke bliver alt for stort.
Problemet kan løses ved at bruge et simpelt neuralt netværk.
Helt grundlæggende handler problemet om, at targetværdi \(t,\) og det udtryk, som vi beregner på baggrund af punktet \(P(x_{m,1}, x_{m,2}, \dots, x_{m,n})\), skal være på samme skala. I det simple neurale netværk brugte vi sigmoid-funktionen \(\sigma\), som aktiveringsfunktion. Forskriften for sigmoid-funktionen er:
\[ \sigma(x)=\frac{1}{1+e^{-x}} \tag{3}\]
og grafen ses i figur 7.
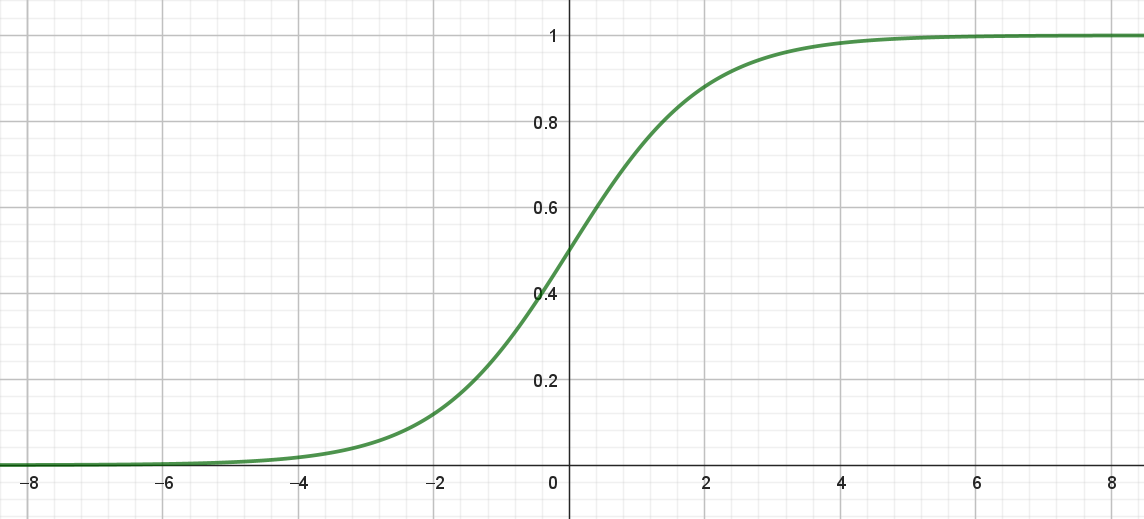
Det centrale her er værdimængden for sigmoid-funktion:
\[ Vm(\sigma)=(0,1). \]
Det vil vi udnytte og nu omdefinere targetværdien \(t\) på denne måde:
\[ t= \begin{cases} 1 & \textrm{hvis punktet er blåt} \\ 0 & \textrm{hvis punktet er rødt} \\ \end{cases} \]
Så targetværdierne er nu \(0\) eller \(1\) i stedet for \(-1\) og \(1\). Vi husker nu, hvordan vi definerede tabsfunktionen for det simple neurale netværk:
\[ \begin{aligned} E(w_0, w_1, &\dots, w_n) \\ &= \frac{1}{2} \sum_{m=1}^{M} \left (t_m- \sigma(w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n}) \right)^2 \end{aligned} \tag{4}\]
Bemærk, at problemet med de to skalaer nu er løst. Targetværdien er enten \(0\) eller \(1\) samtidig med, at \(\sigma(w_0 + w_1 \cdot x_{m,1} + \cdots + w_n \cdot x_{m,n})\) også ligger mellem \(0\) og \(1\). Vi sammenligner altså ikke længere pærer med bananer! Den "perceptron", som minimerer tabsfunktionen i (4), er netop det, vi kalder for et simpelt neuralt netværk.
I noten om simple neurale netværk beskrev vi, hvordan vi kan tænke på outputværdien
\[ o = \sigma(w_0 + w_1 \cdot x_1 + \cdots + w_n \cdot x_n) \]
som en sandsynlighed for at punktet \(P(x_1, x_2, \dots, x_n)\) er blåt. Det gjorde vi på denne måde:
\[ \textrm{Nyt punkt }= \begin{cases} \textrm{blåt} & \textrm{hvis } o \geq 0.5\\ \textrm{rødt} & \textrm{hvis } o < 0.5\\ \end{cases} \tag{5}\]
hvor
\[ o = \sigma(w_0 + w_1 \cdot x_1 + \cdots + w_n \cdot x_n). \]
Vi argumenterede også for, at skillelinjen, for hvornår et punkt \((x_1, x_2, \dots, x_n)\) er blåt eller rødt, kan beskrives ved ligningen
\[ w_0 + w_1 \cdot x_{1} + \cdots + w_n \cdot x_{n} = 0 \]
Tabsfunktionen i simple neurale netværk giver os altså stadigvæk en plan, som kan bruges til at adskille de røde punkter fra de blå.
Lad os prøve først at illustrere det med datasættet bestående af de seks punkter i figur 1. Resultat af at bruge ADALINE (fuldt optrukket linje) og et simpelt neuralt netværk (stiplet linje) ses i figur 8. Det er her tydeligt, at begge metoder kan bruges til at finde en linje, som adskiller de blå punkter fra de røde, og der er i det hele taget ikke den store forskel på de to metoder.
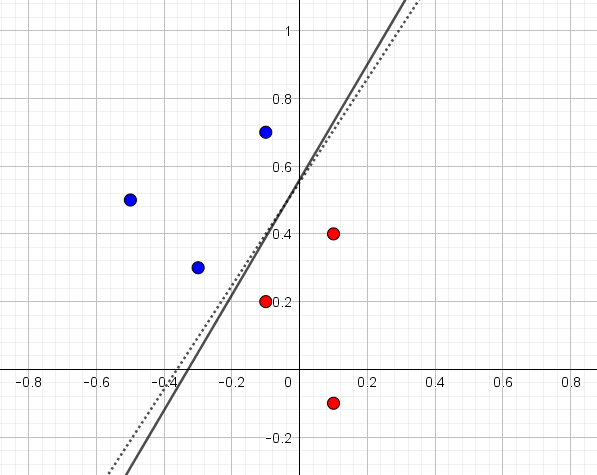
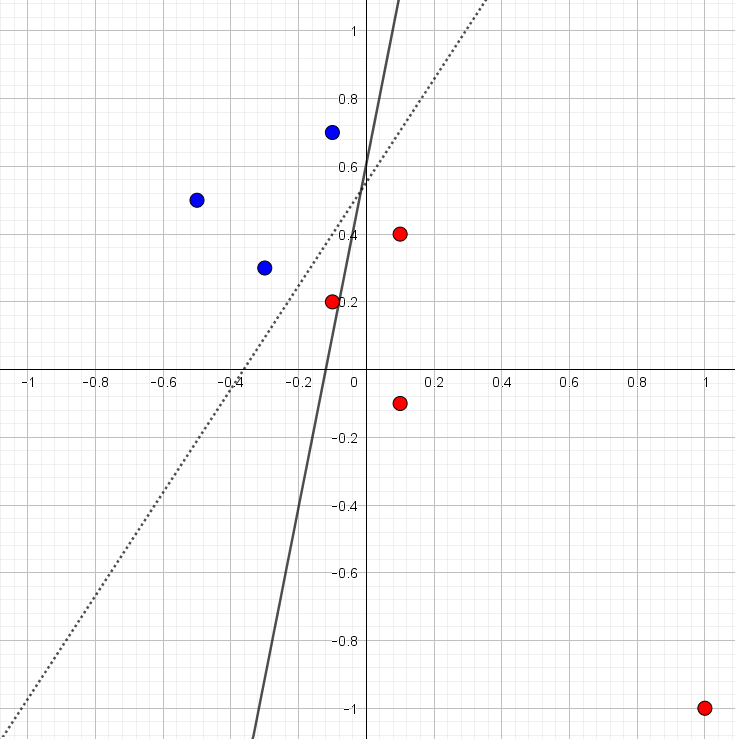
Bruger vi nu ADALINE og et simpelt neuralt netværk på data fra figur 2 fås resultatet i figur 9. Igen svarer ADALINE til fuldt optrukket linje og sigmoid til stiplet linje. Vi kan nu se, at det simple neurale netværk præcis gør det, som vi havde håbet på: Den adskiller de blå punkter fra de røde også selvom ét af punkterne er ekstremt.
Vægtene fra det simple neurale netværk i det sidste eksempel er \(w_0=-6.046\), \(w_1=-16.69\) og \(w_2=10.94\) svarende til linjen med ligning \[ -6.046 - 16.69x_1+10.94x_2=0 \] Udregner vi \[ o = \sigma(-6.046 - 16.69x_1+10.94x_2) \] får vi altså sandsynligheden for at et punkt er blåt. Gør vi det fås resultatet i nedenstående tabel:
| \(x_1\) | \(x_2\) | Targetværdi | Sandsynlighed |
|---|---|---|---|
| \(-0.5\) | \(0.5\) | \(1\) | \(1.00\) |
| \(-0.3\) | \(0.3\) | \(1\) | \(0.90\) |
| \(-0.1\) | \(0.7\) | \(1\) | \(0.96\) |
| \(0.1\) | \(0.4\) | \(0\) | \(0.03\) |
| \(-0.1\) | \(0.2\) | \(0\) | \(0.10\) |
| \(0.1\) | \(-0.1\) | \(0\) | \(0.00\) |
| \(1\) | \(-1\) | \(0\) | \(0.00\) |
Der er her fin overensstemmelse mellem targetværdien og den beregnede sandsynlighed (outputværdien \(o\)). Læg også mærke til at det ekstreme punkt har en beregnet sandsynlighed på \(0.00\) og dermed bliver prædikteret til klart at være et ikke blåt – det vil sige et rødt – punkt.