Når man træner en AI model, sker det som regel ved, at man forsøger at minimere de fejl, som modellen laver, når den anvendes på data, hvor man allerede kender svaret.
For at blive lidt mere konkret så minimerer man en såkaldt tabsfunktion \(E\), som har til formål at "måle", hvor god en AI model1 er. En tabsfunktion \(E\) har altid den egenskab, at \(E \geq 0\), og at en lille værdi af \(E\) svarer til en god model (der er et lille tab), mens en stor værdi af \(E\) svarer til en mindre god model. Derfor vælger man den model, som giver den mindste værdi af tabsfunktionen.
1 Med AI model tænker vi her på en perceptron, et simplet neuralt netværk, et generelt neuralt netværk eller en anden form for funktion, som kan bruges til at prædiktere et eller andet.
AI modellen trænes altså ved at finde minimum for tabsfunktionen. Det gøres ofte ved hjælp af gradientnedstigning – men den konkrete metode er ikke så vigtig lige nu. Det vigtige er her at forstå, at hvis man skal finde minimum for en funktion, så har man brug for at kunne differentiere.
Tabsfunktionen er en sammensat funktion. Den er sammensat af lineære funktioner, som vi kender rigtig godt fra tidligere, andengradspolynomier, og en særlig klasse af funktioner, som kaldes for aktiveringsfunktioner. Og det giver nok mening, at hvis man skal differentiere selve tabsfunktionen, så må man også kunne differentiere den anvendte aktiveringsfunktion \(f\).
Desuden viser det sig vigtigt, at det ikke må være alt for beregningsmæssigt tungt at beregne funktionsværdierne \(f(x)\) og \(f'(x)\). Det skal simpelthen gøres så mange gange – derfor dur det ikke, at det tager for lang tid. Det er derfor ønskværdigt, hvis en aktiveringsfunktions afledede funktion \(f'(x)\) kan beregnes forholdvis simpelt ved hjælp af \(f(x)\). Det betyder nemlig, at hvis vi allerede har udregnet \(f(x)\), så kræver det ikke ret meget også at udregne \(f'(x)\). Det kan illustreres med et eksempel:
Eksempel 1 Funktionen
\[ f(x)=\mathrm{e}^{kx} \]
har afledede funktion
\[ f'(x)=k \cdot \mathrm{e}^{kx} \]
Det vil sige, at vi kan udtrykke \(f'(x)\) ved hjælp af \(f(x)\) på denne måde:
\[ f'(x)= k \cdot f(x). \] Det betyder, at hvis man allerede har udregnet funktionsværdien \(f(x_0)\), så kan man meget nemt udregne tangenthældningen \(f'(x_0)\) i punktet \((x_0,f(x_0))\) ved at gange \(f(x_0)\) med \(k\).
Men ikke alle funktioner har denne egenskab, hvilket det næste eksempel illustrerer:
Eksempel 2 Grafen for funktionen
\[ f(x)=2x^3-3x^2-4x+5 \] ses i figur 1.
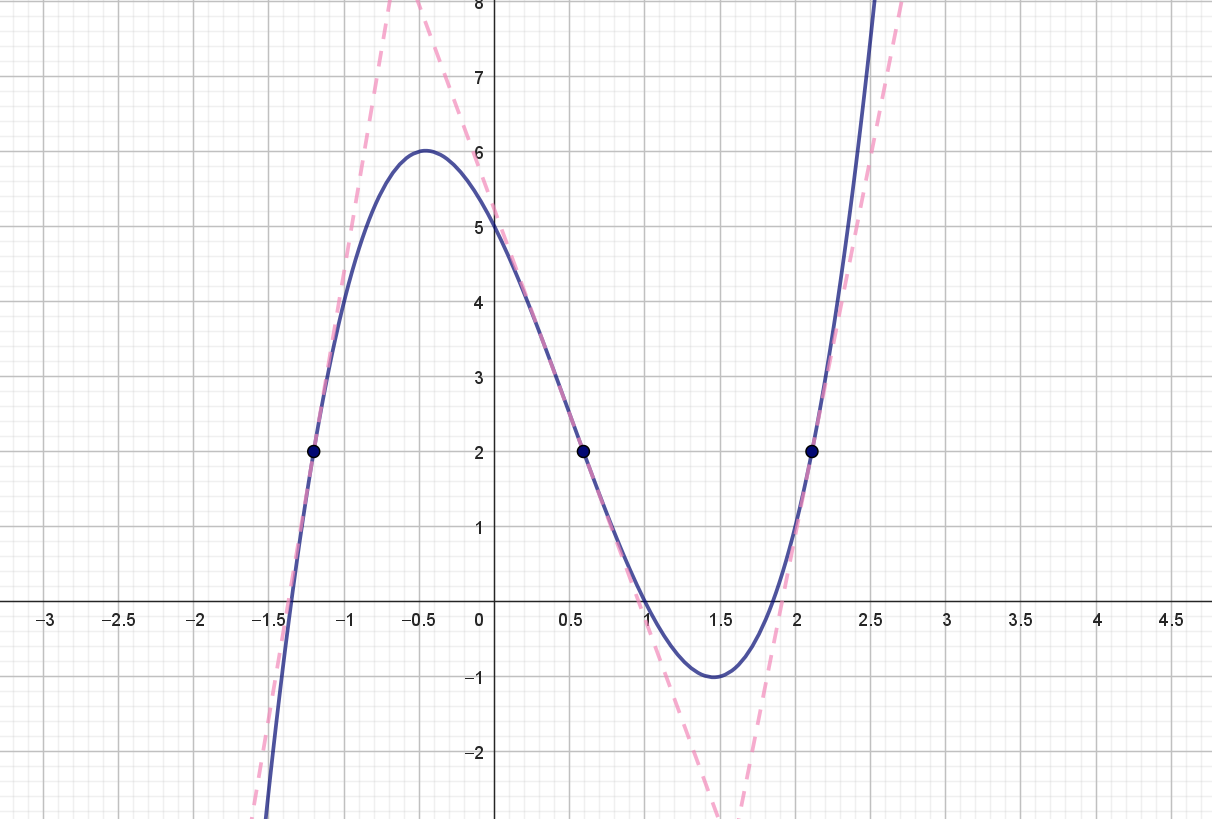
På grafen er der markeret tre punkter, hvor funktionsværdien er \(2\). I disse tre punkter er tangenten til grafen også indtegnet (som stiplede linjer). Her ses det tydeligt, at disse tangenters hældninger ikke er ens. Det betyder derfor, at \(f'(x)\) ikke kan beregnes simpelt alene ud fra funktionsværdien \(f(x)\).
Hvis du vil vide lidt mere om, hvad det der AI egentlig går ud på, så kan du se denne video:
I det nedenstående vil vi nu behandle en række af de mest anvendte aktiveringsfunktioner. Vi finder deres afledede funktioner, og vi vil se, hvordan de afledede funktioner alle kan udtrykkes ved hjælp af den oprindelig aktiveringsfunktion.