Sigmoid-funktionen har forskrift

\[ f(x)=\frac{1}{1+\mathrm{e}^{-x}}, \tag{1}\]

som også kan skrives

\[ f(x)=\frac{\mathrm{e}^x}{1+\mathrm{e}^x}, \] hvilket ses med at gange med \(\mathrm{e}^x\) i både tæller og nævner i (1).

Grafen for Sigmoid-funktionen ses i figur 1.

Figur 1: Grafen for sigmoid-funktionen.

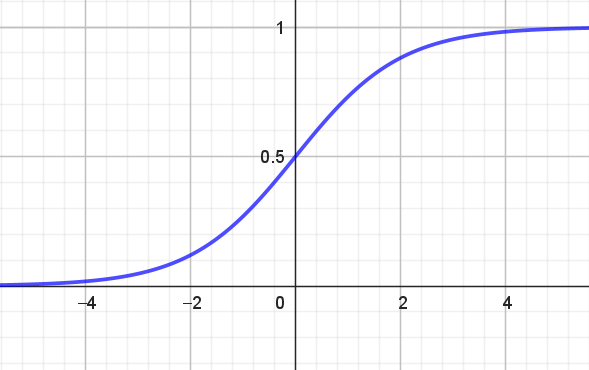
Det ser på figur 1 ud som om, at værdimængden for \(f\) er det åbne interval¹ \((0,1)\). Det skrives

¹ Bemærk, at det åbne interval \((0,1)\) også kan skrives \(]0,1[\).

\[ Vm(f)=(0,1). \]

Hvis du vil have et lidt bedre argument for det, kan du læse i boksen herunder.

Argument for værdimængden for \(f\)

Vi vil her argumentere for, at værdimængden for \(f\) er \((0,1)\). Vi vil starte med at se, at funktionsværdierne for \(f\) ligger mellem \(0\) og \(1\).

Da både tæller og nævner i (1) er positive, så må \(f(x)>0\). Og da

\[ 1<1+\mathrm{e}^{-x} \] så må

\[ \frac{1}{1+\mathrm{e}^{-x}}<\frac{1+\mathrm{e}^{-x}}{1+\mathrm{e}^{-x}}=1. \]

Det vil sige, at \[ 0 < f(x) < 1 \] og derfor må værdimængden for \(f\) være en del af intervallet \((0,1)\). Det kan skrives sådan her

\[ Vm(f) \subseteq (0,1). \] Vi vil nu vise, at vi kan komme lige så tæt på \(0\) og \(1\), som det skal være. Det vil med andre ord sige, at værdimængden for \(f\) "fylder" hele intervallet \((0,1)\) ud.

På figuren herunder ses grafen for \(\mathrm{e}^{-x}\).

Da \(\mathrm{e}^{-x}\) er en aftagende eksponentialfunktion vil

\[ \mathrm{e}^{-x} \rightarrow 0 \quad \textrm{når} \quad x \rightarrow \infty \] og

\[ \mathrm{e}^{-x} \rightarrow \infty \quad \textrm{når} \quad x \rightarrow -\infty. \]

Det betyder, at \[ \frac{1}{1+\mathrm{e}^{-x}} \rightarrow 1 \quad \textrm{når} \quad x \rightarrow \infty \]

og

\[ \frac{1}{1+\mathrm{e}^{-x}} \rightarrow 0 \quad \textrm{når} \quad x \rightarrow -\infty. \]

Alt i alt har vi altså argumenteret for, at værdimængden for \(f\) er \((0,1)\).

De følgende opgaver går ud på at vise, at

\[ f'(x)= \frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^2} \] og at \(f'(x)\) kan udtrykkes ved hjælp af \(f(x)\) på denne måde

\[ f'(x)= f(x)\cdot (1-f(x)). \]

Opgave 1: Differentiation af sigmoid-funktionen

Vis, at \[ f'(x)= \frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^2}. \]

Hints til opgave 1

Vi skal starte med at se, at vi kan tænke på sigmoid-funktionen \[ f(x)=\frac{1}{1+\mathrm{e}^{-x}}. \] som en "dobbelt sammensat" funktion. Sigmoid-funktionen består nemlig af en brøk på formen \(\frac{1}{x}\) og af eksponentialfunktionen \(\mathrm{e}^{-x}\).

Gør følgende:

• Start med at opskrive differentialkvotienten for \[\frac{1}{x} \quad \textrm{og} \quad \mathrm{e}^{-x}.\]

• Brug ovenstående til at vise, at \[ f'(x)= \frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^2}. \]

Opgave 2: Omskrivning af \(f'(x)\) for sigmoid-funktionen

Vis, at \[ f'(x)= f(x)\cdot (1-f(x)). \] når \[ f(x)=\frac{1}{1+\mathrm{e}^{-x}}. \]

Hints til opgave 2

Der er flere fremgangsmåder for at løse opgaven:

Fremgangsmåde 1

• Isolér \(\mathrm{e}^{-x}\) i \[ f(x)=\frac{1}{1+\mathrm{e}^{-x}}. \]

• Indsæt dette udtryk for \(\mathrm{e}^{-x}\) i \[ f'(x)= \frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^2} \] og reducer.

  Hint! Du får brug for at sætte på fælles brøkstreg. Husk også at man dividere med en brøk ved at gange med den omvendte.

Fremgangsmåde 2

• Start med at udregne \[1-f(x).\] Hint! Sæt på fælles brøkstreg ved at skrive \(1\) som \(\frac{1+\mathrm{e}^{-x}}{1+\mathrm{e}^{-x}}\).

• Vis nu at \[ f(x)\cdot (1-f(x)) = \frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^2}=f'(x). \] Husk, at man ganger to brøker med hinanden ved at gange tæller med tæller og nævner med nævner.