Facit til forløbet "Kan vi genkende håndskrevne tal?"
Gennemsnitlig pixelværdi
Ciffer: 0
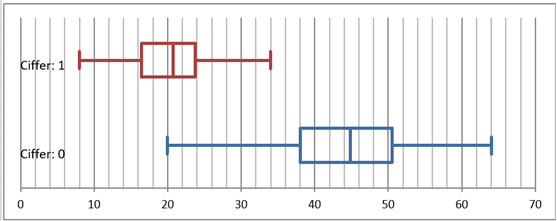
Hvis datasættet grupperes fra \(20\) til \(64\) i intervaller med en bredde på \(2\) fås det udvidede kvartilsæt til:
\[ (20.57, 38.55, 44.65, 51.09, 63.04) \]
Ciffer: 1
Hvis datasættet grupperes fra \(8\) til \(34\) i intervaller med en bredde på \(2\) fås det udvidede kvartilsæt til:
\[ (9.62, 16.375, 20.79, 23.62, 33.09) \] Boksplots
Antal hvide pixels
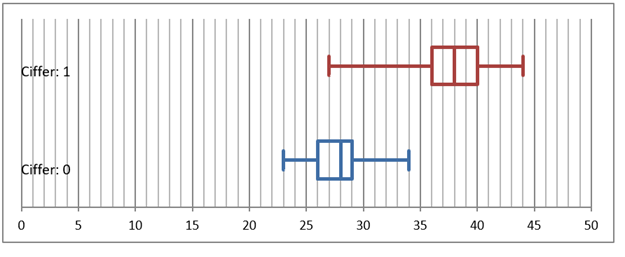
Ciffer: 0
Hvis datasættet ikke grupperes fås det udvidede kvartilsæt til:
\[ (23, 26, 28, 29, 34) \]
Ciffer: 1
Hvis datasættet ikke grupperes fås det udvidede kvartilsæt til:
\[ (27, 36, 38, 40, 44) \]
Gennemsnitlig pixelværdi
Ved \(x=30.2\) bliver 5 klassificeret forkert. Det giver en klassifikationsnøjagtighed på \(97.5 \%\).
Antal hvide pixels
Ved \(y=31.5\) bliver 3 klassificeret forkert. Det giver en klassifikationsnøjagtighed på \(98.5 \%\).
Begge features
Det kan ikke gøres bedre, selvom vi bruger begge features.
Hvis man bruger en pixelopløsning på \(14 \times 14\) eller \(28 \times 28\) pixels bliver mindst 4 cifre klassificeret forkert.
Det er helt umuligt at kende forskel på 0 og 3-taller, hvis man bruger den gennemsnitlige pixelværdi og antallet af hvide pixels. Dette er illustreret her:
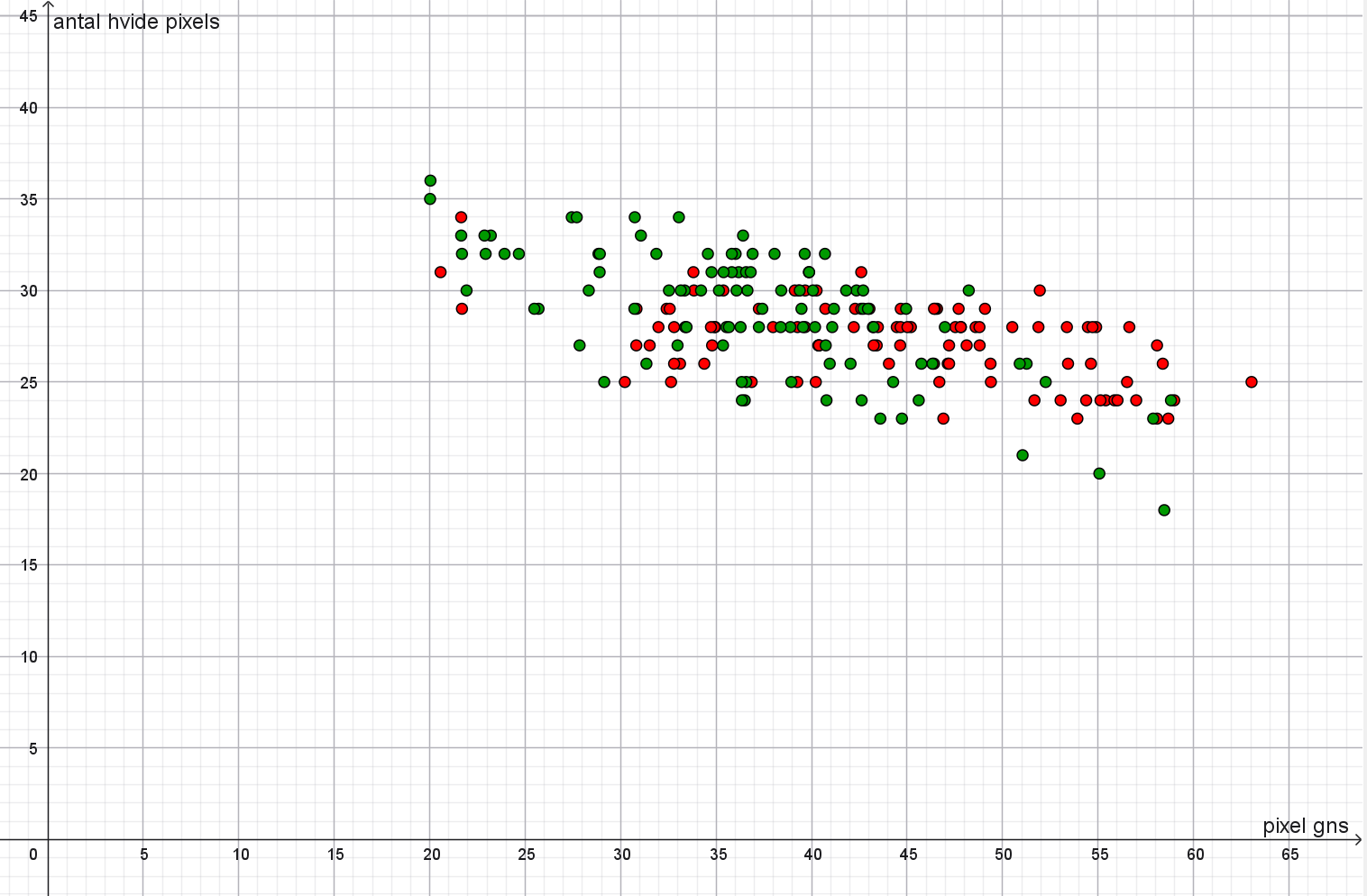
Plot af \((\textrm{lodret}_\textrm{gns}, \textrm{vandret}_\textrm{gns})\):
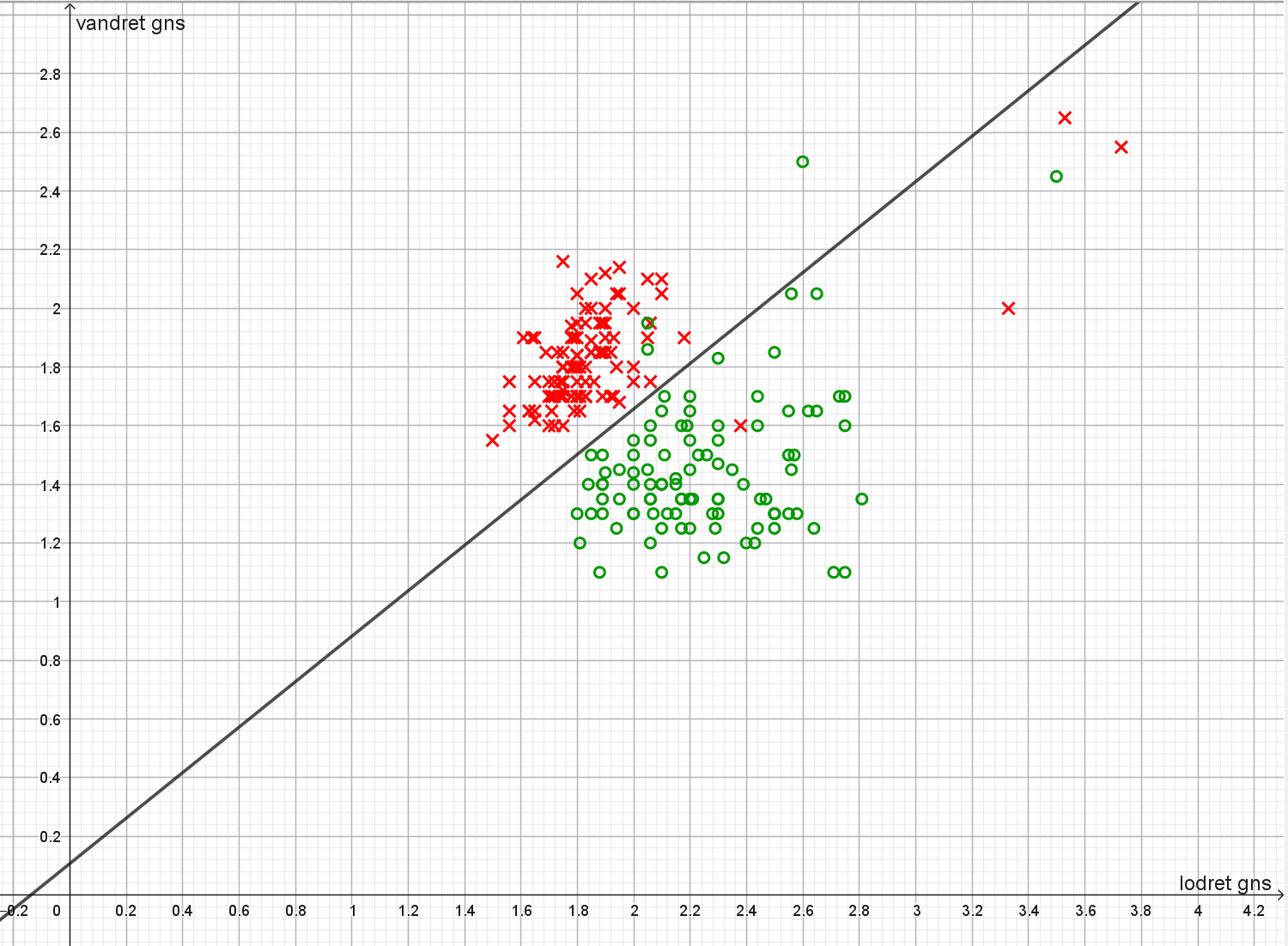
Det kan ikke lade sig gøre at klassificere cifrene med id 3, 8, 35, 54, 327, 344, 398 korrekt.
Klassifikationsnøjagtigheden er \(96.5 \%\).
Plot af \((\textrm{lodret}_\textrm{gns}, \textrm{vandret}_\textrm{gns})\) baseret på en pixel-opløsning på \(7\):
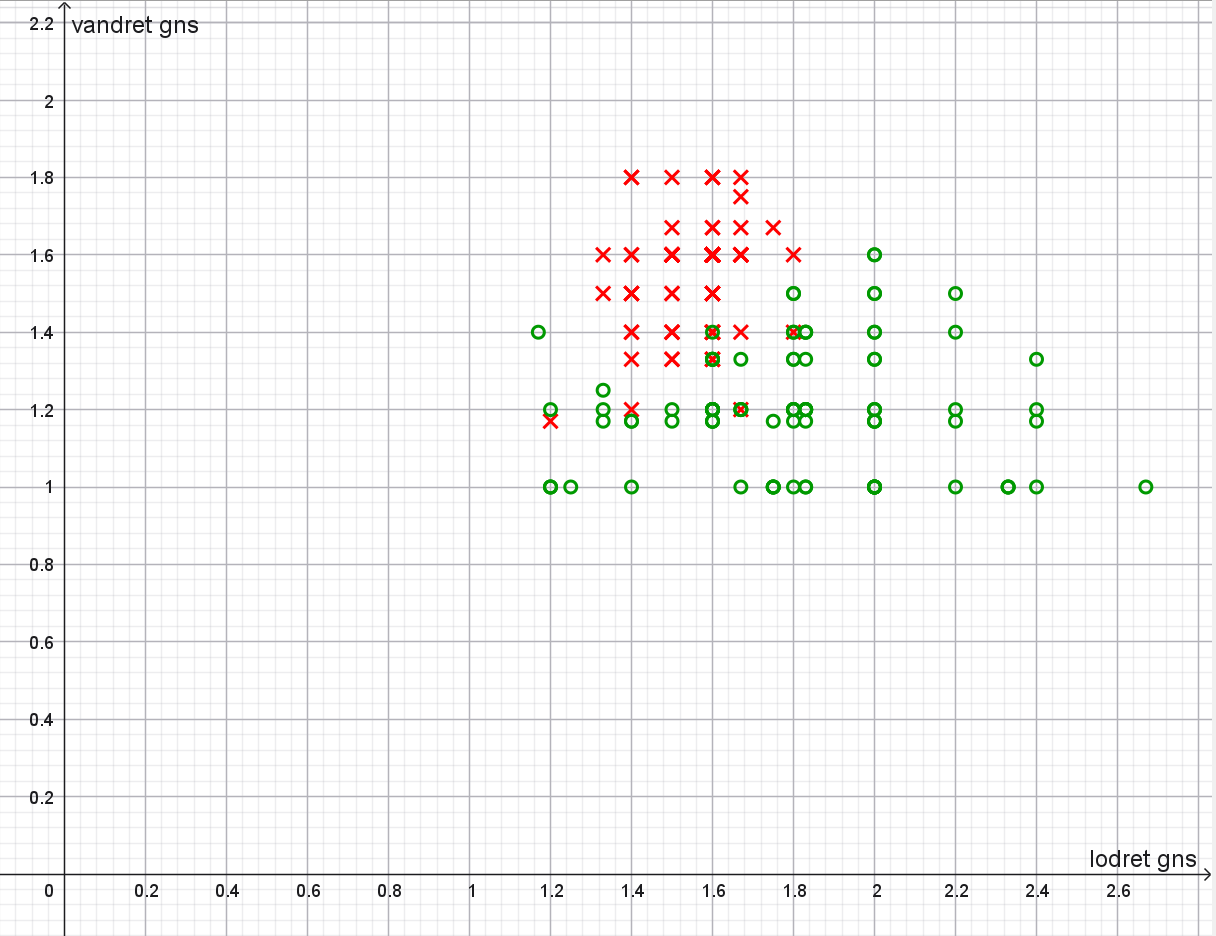
Som det kan ses på ovenstående plot, giver en pixel-opløsning på \(7\) faktisk anledning til flere fejl! Det vil sige, at klassifikationsnøjagtigheden falder.
Plot af \((\textrm{lodret}_\textrm{gns}, \textrm{vandret}_\textrm{gns})\) baseret på en pixel-opløsning på \(14\):
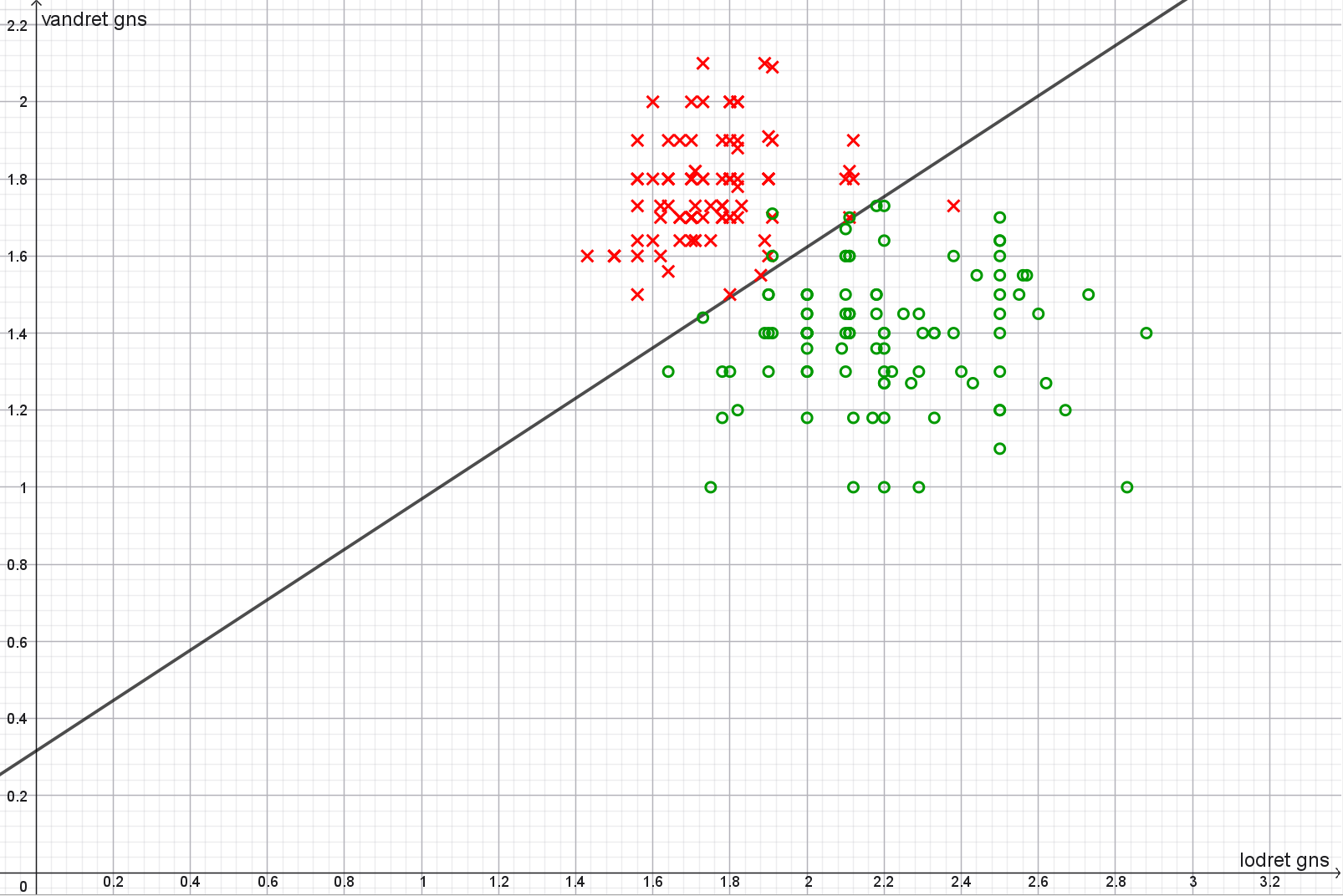
Her kan vi komme helt ned på fire cifre (id 8, 326, 327, 329), som misklasifficeres. Det giver en klassifikationsnøjagtighed på \(98 \%\).