Inddeling af musik i grupper
Formål
I dette forløb vil vi se på, hvordan en algoritme, der hedder K-means, kan anvendes til at inddele musiknumre i grupper, for eksempel for at en musiktjeneste kan give anbefalinger til ny musik, som man sikkert gerne vil høre.
Midterpunkt
Inden vi går i gang med musiknumre, skal vi se på, hvordan man kan finde midterpunktet for en gruppe af punkter. Hvis vi for eksempel har fire punkter med koordinatsæt:
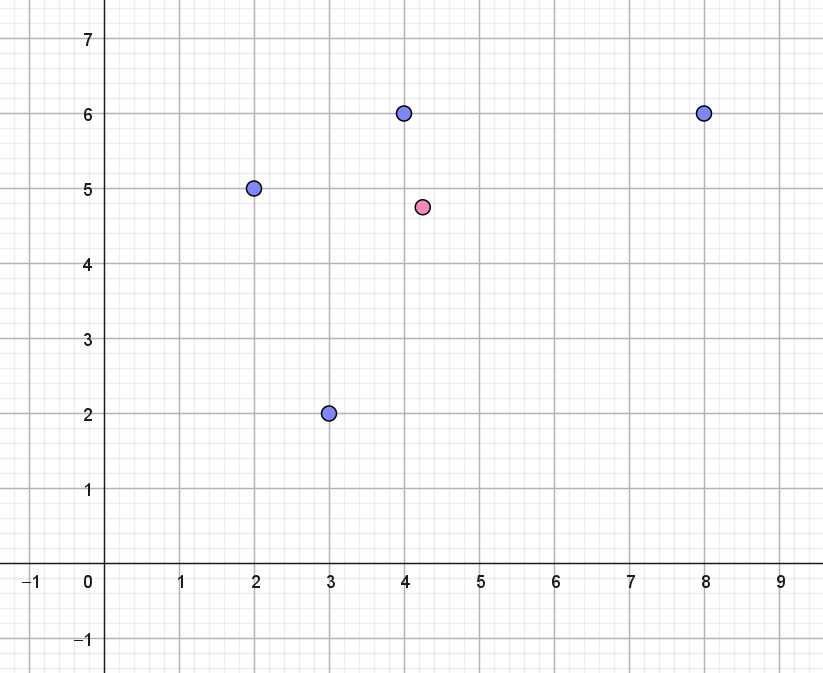
\[ (3,2) \qquad (8,6) \qquad (4,6) \qquad (2,5) \] så kan vi beregne denne gruppes midterpunkt ved at tage gennemsnittet af alle \(1.\) koordinaterne samt gennemsnittet af alle \(2.\) koordinaterne. Dette vil give koordinatsættet til midterpunktet:
\[ \left ( \frac{3+8+4+2}{4}, \frac{2+6+6+5}{4} \right)=(4.25, 4.75) \]
På figur 1 ses de fire punkter (blå) og midterpunktet (lyserødt). Læg mærke til, hvordan midterpunktet pænt ligger midt blandt de fire andre punkter.
K-means til inddeling af musiknumre i grupper
For at kunne opdele musiknumre i grupper er det nødvendigt at finde nogle informationer (også kaldet for features) til hvert nummer. En oplagt information kunne umiddelbart være musikgenre: Rock, pop, klassisk, country og så videre.
Når man skal lave en opdeling af nogle musiknumre, bliver opdelingen foretaget af en computer, som også selv kan analysere musiknumrene og finde featureværdier. Nogle af de features, man kan bruge er: Lydniveau, energi, instrumentalitet, dansbarhed, positivitet og tempo.
For at anvende algoritmen K-means, skal alle features først og fremmest være talværdier. Derudover bør hver feature enten være angivet på samme skala, for eksempel fra \(0\) til \(1\), eller ændres ved hjælp af en metode, som kaldes for feature-skalering, som gør, at hver feature får lige stor betydning.
Her ses på et mindre eksempel med 15 musiknumre, man ønsker at opdele i tre grupper ud fra tre features: Danceabilty, energy og speechiness.
| Nummer | Danceability | Energy | Speechiness | Gruppe |
|---|---|---|---|---|
| Barbie Girl | \(0.76\) | \(0.95\) | \(0.04\) | \(1\) |
| Shape of You | \(0.83\) | \(0.65\) | \(0.08\) | \(2\) |
| Set Fire to the Rain | \(0.60\) | \(0.67\) | \(0.02\) | \(3\) |
| Wake Me Up | \(0.53\) | \(0.78\) | \(0.05\) | \(1\) |
| Baby One More Time | \(0.76\) | \(0.70\) | \(0.03\) | \(2\) |
| Just The Way You Are | \(0.64\) | \(0.84\) | \(0.04\) | \(3\) |
| New Rules | \(0.76\) | \(0.72\) | \(0.07\) | \(1\) |
| Stan | \(0.78\) | \(0.74\) | \(0.21\) | \(2\) |
| In Da Club | \(0.90\) | \(0.71\) | \(0.37\) | \(3\) |
| Blinding Lights | \(0.51\) | \(0.80\) | \(0.06\) | \(1\) |
| Blank Space | \(0.76\) | \(0.70\) | \(0.05\) | \(2\) |
| Dance Monkey | \(0.82\) | \(0.59\) | \(0.09\) | \(3\) |
| Hotline Bling | \(0.90\) | \(0.62\) | \(0.06\) | \(1\) |
| Die To Live | \(0.42\) | \(0.97\) | \(0.14\) | \(2\) |
| White Iverson | \(0.67\) | \(0.52\) | \(0.04\) | \(3\) |
Numrene er her placeret i en tilfældig af de tre grupper fra start, så algoritmen har et sted at starte. Opgaven er så, at numrene skal inddeles på en måde, så rimeligt ens numre kommer i samme gruppe. Der behøver ikke være lige mange numre i hver gruppe i den færdige inddeling, men der skal være tre grupper med numre i vores eksempel.
Fordi alle musiknumrene er repræsenteret ved tre features, kan vi tænke på hvert nummer, som et punkt i et 3-dimensionelt koordinatsystem. For eksempel svarer nummeret "Barbie Girl" til punktet med koordinatsæt \((0.76, 0.95, 0.04)\).
Idéen er nu, at vi udregner et midterpunkt for alle numrene i gruppe 1, et andet midterpunkt for alle numrene i gruppe 2 og et tredje midterpunkt for alle numrene i gruppe 3. Da vores punkter nu har tre koordinater, findes midterpunktet ved at tage gennemsnittet af henholdsvis alle \(1.\), \(2.\) og \(3.\) koordinater.
Herefter vil vi se på hvert enkelt nummer og afgøre, hvilket af de tre midterpunkt, nummeret ligger tættest på. Hvis nummeret ligger tættest på midterpunktet for den gruppe, nummeret allerede er i, sker der ikke noget. Hvis nummeret derimod ligger tættest på midterpunktet for en af de andre grupper, bliver nummeret flyttet til den pågældende gruppe. Dette er idéen bag K-means, som vi kan opsummere sådan her:
K-means algoritmen
Start med at sætte alle musiknumre i en tilfældig af de tre grupper.
Udregn midterpunktet for hver af de tre grupper.
Udregn for hvert musiknummer afstanden fra det punkt, som repræsenterer musiknummeret, til hver af de tre midterpunkter. Placér musiknummeret i den gruppe, hvis midterpunkt nummeret er tættest på.
Gentag punkt 2 og 3, indtil ingen musiknumre skifter gruppe.
K-means algoritmen er et eksempel på det, som man kalder for unsupervised learning, fordi vi ikke på forhånd har nogle informationer om, hvilke musiknumre som passer sammen.
Vi skal altså nu for hvert enkelt nummer have undersøgt, hvilket af de tre midterpunktet, nummeret ligger tættest på. Du kender allerede formlen for afstand mellem to punkter i planen, hvor hvert punkt har to koordinater
\[P(x_1,y_1) \qquad \textrm{og} \qquad Q(x_2,y_2)\]
Da er afstanden mellem \(P\) og \(Q\):
\[ |PQ|= \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2} \]
Når der er tre koordinater:
\[P(x_1,y_1,z_1) \qquad \textrm{og} \qquad Q(x_2,y_2,z_2)\] udvides formlen blot med et led mere under kvadratrodstegnet:
\[ |PQ|= \sqrt{(x_2-x_1)^2+(y_2 - y_1)^2+(z_2 - z_1)^2} \]
Herunder er afstanden til de tre midterpunkter beregnet for alle numrene.
| Nummer | Afstand midterpunkt 1 | Afstand midterpunkt 2 | Afstand midterpunkt 3 | Opr. gruppe | Ny gruppe |
|---|---|---|---|---|---|
| Barbie Girl | \(0.189\) | \(0.213\) | \(0.295\) | \(1\) | |
| Shape of You | \(0.187\) | \(0.159\) | \(0.110\) | \(2\) | |
| Set Fire to the Rain | \(0.143\) | \(0.160\) | \(0.156\) | \(3\) | |
| Wake Me Up | \(0.162\) | \(0.189\) | \(0.235\) | \(1\) | |
| Baby One More Time | \(0.104\) | \(0.102\) | \(0.095\) | \(2\) | |
| Just The Way You Are | \(0.086\) | \(0.128\) | \(0.207\) | \(3\) | |
| New Rules | \(0.088\) | \(0.067\) | \(0.076\) | \(1\) | |
| Stan | \(0.181\) | \(0.129\) | \(0.134\) | \(2\) | |
| In Da Club | \(0.382\) | \(0.331\) | \(0.314\) | \(3\) | |
| Blinding Lights | \(0.184\) | \(0.210\) | \(0.259\) | \(1\) | |
| Blank Space | \(0.101\) | \(0.089\) | \(0.078\) | \(2\) | |
| Dance Monkey | \(0.227\) | \(0.196\) | \(0.123\) | \(3\) | |
| Hotline Bling | \(0.259\) | \(0.235\) | \(0.187\) | \(1\) | |
| Die To Live | \(0.346\) | \(0.365\) | \(0.432\) | \(2\) | |
| White Iverson | \(0.255\) | \(0.243\) | \(0.172\) | \(3\) |
Beregningerne skal så gentages, typisk mange gange, indtil der ingen ændringer sker. Når algoritmen har fået inddelt alle numrene i tre grupper, så yderligere en omgang beregninger ikke flytter numrene mellem grupperne, er algoritmen færdig. Men det kan godt kræve rigtigt mange beregninger, som vi derfor ikke vil lave manuelt.
Hvis du er god til regneark, for eksempel Excel, kan du få Excel til smart at lave beregningerne. Alternativt kan du bruge et gratis program Orange, som vi også bruger til andre forløb her på siden.
Tag udgangspunkt i det punktplot, som du lavede i opgave 3.
- Farvelæg punkterne, så punkter i samme inddeling får samme farve.
Sådan gør du i GeoGebra
Gå ind i regnearket og tilføj en søjle (i
E), som angiver hvilken gruppe musiknummeret er kommet i.Stil dig i celle
F2, højreklik og vælg "Egenskaber". Vælg herefter fanen "Avanceret".I det felt, hvor der står "Rød", skriver du
If(E2==1,1,0).I det felt, hvor der står "Grøn", skriver du
If(E2==2,1,0).I det felt, hvor der står "Blå", skriver du
If(E2==3,1,0).
Det kommer til at se sådan her ud (hvis du har GeoGebra på dansk bliver "If" lavet om til "Hvis"):
- Marker igen celle
F2og tag ved den lille kasse i nederste hjørne af celleF2og trække ned, så du får udfyldt kolonneFfor hele datasættet. Alle punkterne skulle nu gerne være farvet som ønsket.
- Når du drejer rundt i dit 3-dimensionale koordinatsystemer, giver inddelingen af punkterne så mening i forhold til punkternes placering?