Del 2: Gradientnedstigning

Forventet tid ca. 1 x 90 min.




Aktivitet 1 - Kunstige neuroner

Læs afsnittet "Medlemsapp til Good Food" i noten om kunstige neuroner.

Opgave 1: Arbejdsspørgsmål til noten

Forklar med dine egne ord, hvad følgende betyder:

  • Targetværdi
  • Outputværdi
  • Træningsdatasæt
  • Tabsfunktion




Aktivitet 2 - Gradientnedstigning

Læs afsnittet "Hvordan bestemmes vægtene" i noten om kunstige neuroner (du behøver ikke at forstå alt i afsnittet - de "vilde" udregninger i forhold til at differentiere kan du for eksempel bare spring over!).

Vi vil illustrere gradientnedstigning i et simpelt eksempel:

Opgave 2: Minimum for en funktion af to variable

Lad os se på en funktion \(f\), som afhænger af to variable \(x\) og \(y\) (i noten om kunstige neuroner svarer de to variable til et eksempel med to vægte \(w_0\) og \(w_1\)):

\[ f(x,y)= 0.2x^2-1.2x+0.3y^2-2.4y+8.6 \]

  • Tegn grafen for funktionen i GeoGebra (her skriver man forskriften ind i inputfeltet og vælger derefter "Vis" \(\rightarrow\) "3D Grafik").

Tænk på grafen som en skibakke. Nede i bunden af bakken er der "After Ski", så der vil du selvfølgelig gerne ned! Det svarer matematisk til funktionens minimum.

  • Hvis du kigger på grafen alene - hvad er så dit bedste bud på minimumsstedet \((x,y)\) (altså i hvilket \((x,y)\)-koordinat ser det ud til, at "After Ski" ligger)?

Vi vil nu bruge gradientnedstigning til at bestemme minimum.

Opgave 3: Opdateringsregler

  • Bestem de såkaldte partielle afledede \(\frac{\partial f}{\partial x}\) og \(\frac{\partial f}{\partial y}\). Når du for eksempel skal finde \(\frac{\partial f}{\partial x}\), så skal du differentiere \(f(x,y)\), hvor du tænker på \(x\) som den variable og \(y\) som en konstant. Tilsvarende med \(\frac{\partial f}{\partial y}\).

  • Brug de partielle afledede til at opskrive opdateringsreglerne:

    \[ \begin{aligned} x^{(\textrm{ny})} &\leftarrow x - \eta \cdot \frac{\partial f}{\partial x} \\ y^{(\textrm{ny})} &\leftarrow y - \eta \cdot \frac{\partial f}{\partial y} \end{aligned} \]

Nu stiller vi os et tilfældigt sted på skibakken – lad og sige i punktet \((6,8,f(6,8))\).

  • Udregn funktionsværdien \(f(6,8)\) og indtegn punktet \((6,8,f(6,8))\) i dit koordinatsystem (i GeoGebra skriver du bare (6,8,f(6,8))).

Du skal nu bruge ovenstående opdateringsregler til at finde ned mod "After Ski". Vi beslutter os for at vælge en skridtlængde på \(\eta = 0.1\). Den første opdatering bliver så:

\[ \begin{aligned} x^{(\textrm{ny})} &\leftarrow 6 - 0.1 \cdot \frac{\partial f}{\partial x}(6,8) \\ y^{(\textrm{ny})} &\leftarrow 8 - 0.1 \cdot \frac{\partial f}{\partial y}(6,8) \end{aligned} \]

Hint! Her er \[\frac{\partial f}{\partial x}(6,8)=0.4 \cdot 6-1.2= 1.2\] og \[\frac{\partial f}{\partial y}(6,8)=0.6 \cdot 8-2.4=2.4\]

  • Udregn \(x^{(\textrm{ny})}\), \(y^{(\textrm{ny})}\) og funktionsværdien \(f(x^{(\textrm{ny})}, y^{(\textrm{ny})})\). Er funktionsværdien blevet mindre sammenlignet med \(f(6,8)\)?

  • Indtegn punktet \((x^{(\textrm{ny})},y^{(\textrm{ny})},f(x^{(\textrm{ny})},y^{(\textrm{ny})}))\) i dit koordinatsystem. Kan du se, at du er på vej ned mod skibakken?

Det bliver lidt tungt at skulle lave disse udregninger i hånden. Vi vil derfor gøre det i Excel eller i GeoGebras regneark. I den næste opgave forklarer vi, hvordan man gør i GeoGebra:

Opgave 4: Gradientnedstigning i GeoGebra

  • Udfyld et regneark på denne måde:

    • I celle A1 skriver du 6 (svarende til \(x=6\), der hvor vi starter).
    • I celle B1 skriver du 8 (svarende til \(y=8\)).
    • I celle C1 skriver du f(A1,B1) (det kræver, at du allerede har defineret funktionen i inputfeltet).
    • I celle D1 skriver du (A1,B1,C1) (læg mærke til at punktet bliver tegnet ind i koordinatsystemet).

Vi skal nu have skrevet opdateringsreglerne ind. Du har nok tidligere fået, at \[ \frac{\partial f}{\partial x}=0.4x-1.2 \]

og

\[ \frac{\partial f}{\partial y}=0.6y-2.4 \]

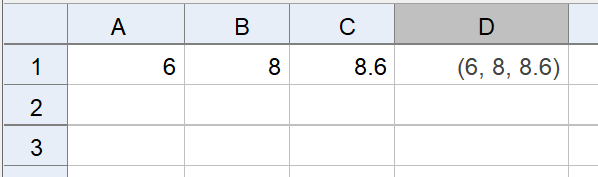
  • Du skal udvide regnearket på denne måde:

    • I celle A2 skriver du = A1 - 0.1*(0.4*A1-1.2).
    • I celle B2 skriver du = B1 - 0.1*(0.6*B1-2.4).
    • I celle C2 skriver du f(A2,B2).
    • I celle D2 skriver du (A2,B2,C2).

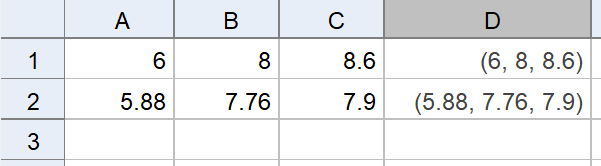
  • Du kan nu markere række to, tage ved den lille kasse i nederste højre hjørne og trække ned for at beregne nye punkter. Gør det!

  • Hvor mange opdateringer skal du lave, for at funktionsværdien ikke ser ud til at ændre sig mere?

  • Svarer det minimum, du finder ved hjælp af gradientnedstigning til det minimum, som du tidligere har aflæst på grafen?

Tillykke! Du er nu kommet til "After Ski"!!