Opdatering af vægte i et simpelt neuralt netværk med ét skjult lag (men med cross-entropy som tabsfunktion)

Forudsætninger og tidsforbrug

• Neurale netværk.
• Sigmoid aktiveringsfunktion.
• Gradientnedstigning.
• Cross-entropy tabsfunktion.

Forudsætningerne kan med fordel dækkes ved hjælp af noten om simple neurale netværk, da notationen derfra vil blive anvendt i dette forløb, samt noten om tabsfunktioner.

Dette forløb ligner forløbet om opdatering af vægte i neuralt netværk med to skjulte lag, men er lidt sværere, da man desuden skal modificere nogle elementer i forhold til noten om simple neurale netværk.

Tidsforbrug: Ca. 90 minutter.

Formål

Formålet med dette forløb er gennem detaljerede beregninger at forstå, hvordan vægtene i et neuralt netværk til klassifikation med ét skjult lag opdateres med brug af sigmoid aktiveringsfunktionen og gradientnedstigning med cross-entropy som tabsfunktion.

Dette kan ses som et skridt på vejen til at forstå, hvordan vægtene opdateres i et generelt neuralt netværk.

Et meget lille datasæt

I neurale netværk er der ofte rigtige mange inputvariable (features), rigtigt mange vægte og rigtig mange træningsdata.

For bedre at forstå, hvor vægtene opdateres i et neuralt netværk, vil vi her se på et meget lille eksempel, så det manuelt er muligt at lave opdateringen af vægtene.

Vi vil lave et netværk med 2 inputvariable (\(x_1\) og \(x_2\)), 1 neuron i det skjulte lag (\(y\)) og 1 neuron i outputlaget (\(o\)). Netværket er illustreret i figur 1.

Figur 1: Grafisk illustration af et neuralt netværk med 2 inputvariable og ét skjulte lag, som består af én neuron.

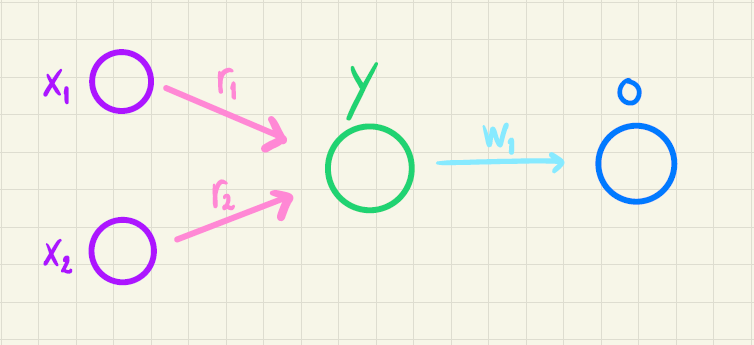
Konkret vil vi se på to features \(x_1\) og \(x_2\) og en targetværdi \(t\) ud fra følgende træningsdatasæt:

\(x_1\)	\(x_2\)	\(t\)
1	2	0
2	3	1
3	7	0

Vi vælger en learning rate på

\[\eta = 0.1,\]

sigmoid-funktionen som aktiveringsfunktion

\[\sigma(x)=\frac{1}{1+e^{-x}}\]

og cross-entropy som tabsfunktion \[ E = - \sum_{m=1}^{M} \left( (t^{(m)} \cdot \ln(o^{(m)}) + (1-t^{(m)}) \cdot \ln(1-o^{(m)}) \right) \] Endeligt vælger vi startvægtene fra inputlaget til det skjulte lag som

\[ r_0=0.5 \textrm{ (bias)},\qquad r_1=0.5,\qquad r_2=0.5 \]

og fra det skjulte lag til outputlaget som

\[ w_0=0.5 \textrm{ (bias)}, \qquad w_1=0.5 \]

Plan

Planen er nu følgende:

• Lav feedforward fra \(x\) laget til \(y\) laget.

• Lav feedforward fra \(y\) laget til \(o\) laget.

• Opskriv opdateringsregler for \(w\)-vægtene.

• Opdatér \(w\)-vægtene.

• Opskriv opdateringsregler for \(r\)-vægtene.

• Opdatér \(r\)-vægtene.

Opgaver

Opgave 1: Feedforward fra \(x\) til \(y\) lag

• Udregn

  \[r_0 + r_1 \cdot x_1^{(m)} + r_2 \cdot x_2^{(m)}\]

  for hver af de 3 træningseksempler.

• Udregn

  \[y^{(m)}=\sigma(r_0 + r_1 \cdot x_1^{(m)} + r_2 \cdot x_2^{(m)})\]

  for hver af de 3 træningseksempler.

Opgave 2: Feedforward fra \(y\) til \(o\) lag

• Udregn på tilsvarende vis \(o^{(m)}\) for hver af de 3 træningseksempler.

Opgave 3: Opskriv opdateringsregler for \(w\)-vægtene

• Opskriv opdateringsreglen for \(w_0\) og \(w_1\). Husk, at

  • sigmoid-funktionen har følgende egenskab: \(\sigma'(x)=\sigma(x) \cdot (1-\sigma(x))\)
  • tabsfunktionen er cross-entropy.

Opgave 4: Opdatér \(w\)-vægtene

• Udregn

  \[\delta_w^{(m)} = t^{(m)}-o^{(m)}\]

• Udregn

  \[\sum_{m=1}^{3} \delta_w^{(m)}\]

• Opdatér \(w_0\)-vægten

  \[w_0^{ny} \leftarrow w_0 + \eta \cdot \sum_{m=1}^{3} \delta_w^{(m)}\]

• Udregn

  \[\sum_{m=1}^{3} \delta_w^{(m)} \cdot y^{(m)}\]

• Opdatér \(w_1\)-vægten

  \[w_1^{ny} \leftarrow w_1 + \eta \cdot \sum_{m=1}^3 \delta_w^{(m)} \cdot y^{(m)}\]

Opgave 5: Opskriv opdateringsregler for \(r\)-vægtene

• Opskriv opdateringsreglen for \(r_0, r_1\) og \(r_2\).

Opgave 6: Opdatér \(r\)-vægtene

• Lav udregninger tilsvarende dem i opgave 4 og opdatér af \(r\)-vægtene.

Opgave 7: Udregn værdien af tabsfunktionen

• Udregn værdien af tabsfunktionen inden opdateringen.

• Udregn værdien af tabsfunktionen efter opdateringen.

Værdien skulle meget gerne være blevet mindre med opdateringen.

Anden opdatering af vægtene

Overvej, om du kan strømline dine beregninger, eventuelt i Excel eller i dit CAS værktøj, så det bliver hurtigere at opdatere vægtene en gang mere på samme måde.

Opgave 8: Opdater vægtene anden gang

• Beregn de opdaterede vægte.

• Beregn tabsfunktionen på de opdaterede vægte.

Bemærk, at værdien af tabsfunktionen er blevet lidt mindre. Formålet er jo netop at minimere den gennem gradientnedstigning, så som regel bør værdien bliver mindre, hver gang vægtene opdateres.

Løsninger til opgaver

Facitliste.