Aktiveringsfunktionen ReLU som står for Reflected Linear Unit har forskrift
\[ f(x) = \begin{cases} x & \textrm{hvis } x > 0 \\ 0 & \textrm{hvis } x \leq 0 \\ \end{cases} \] og grafen for ReLU-funktionen ses i figur 1.
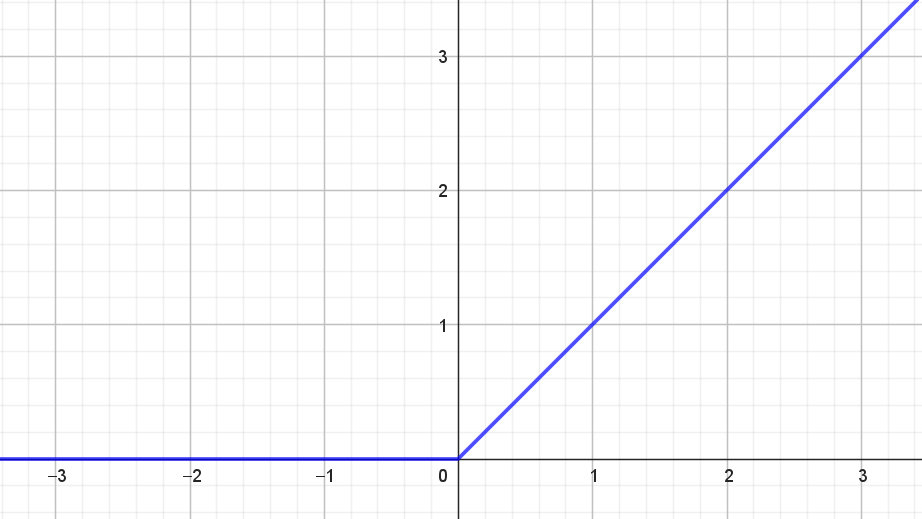
Værdimængden for ReLU-funktionen er \([0, \infty)\).
Det er ret tydeligt, at ReLU-funktionen ikke er differentiabel i \(0\). Men hvis vi definerer, at \(f'(0)\) skal være \(0\) så ses det nemt, at
\[ f'(x) = \begin{cases} 1 & \textrm{hvis } x > 0 \\ 0 & \textrm{hvis } x \leq 0 \\ \end{cases}. \]
ReLU-funktionen adskiller sig fra de andre aktiveringsfunktioner ved, at værdimængden er ubegrænset. Hvis man ønsker at bruge aktiveringsfunktionen til at modellere en sandsynlighed, som beskrevet tidligere, så dur det selvfølgelig ikke. Men i praksis viser ReLU-funktionen sig at være utrolig anvendelig som aktiveringsfunktion i de skjulte lag i kunstige neurale netværk. For det første kan nogle af de andre aktiveringsfunktioner resultere i det, vi i afsnittet om valg af tabsfunktion i noten om kunstige neurale netværk, kalder for slow learning. Det betyder kort sagt, at det går for langsomt med at finde minimum for tabsfunktionen. Dét problem har ReLU-funktionen ikke. For det andet er det meget hurtigt og nemt at udregne både ReLU-funktionen selv og også dens afledede. Det er for eksempel til sammenligning beregningsmæssigt tungere at udregne sigmoid-funktionen og dennes afledede. Hvis man har et netværk med millioner af neuroner, så er denne beregningsmæssige forskel ikke uvæsentlig.