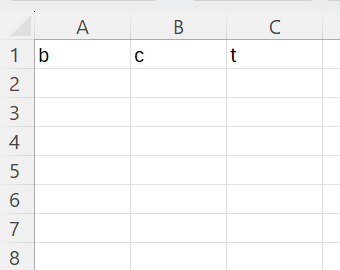
AI og rødder i andengradspolynomier
Formål
Et andengradspolynomium kan have enten ingen, én eller to rødder. Vi vil her undersøge,om man mon kan bruge kunstig intelligens til at bestemme antallet af rødder i et andengradspolynomium.
Formålet er dog ikke at bruge eksisterende AI metoder til at bestemme antallet af rødder, men derimod at I selv får kendskab til, hvordan sådan nogle metoder fungerer. I skal altså lære lidt om nogle af de principper, der ligger bag diverse AI algoritmer.
Andengradspolynomier og rødder
Lad os lige starte med at minde om, at et andengradspolynomium er en funktion med en forskrift på formen \[ f(x)=ax^2 + bx + c, \quad a \neq 0 \] Grafen for et andengradspolynomium kaldes som bekendt for en parabel. I figur 1 ses tre eksempler på sådanne parabler.
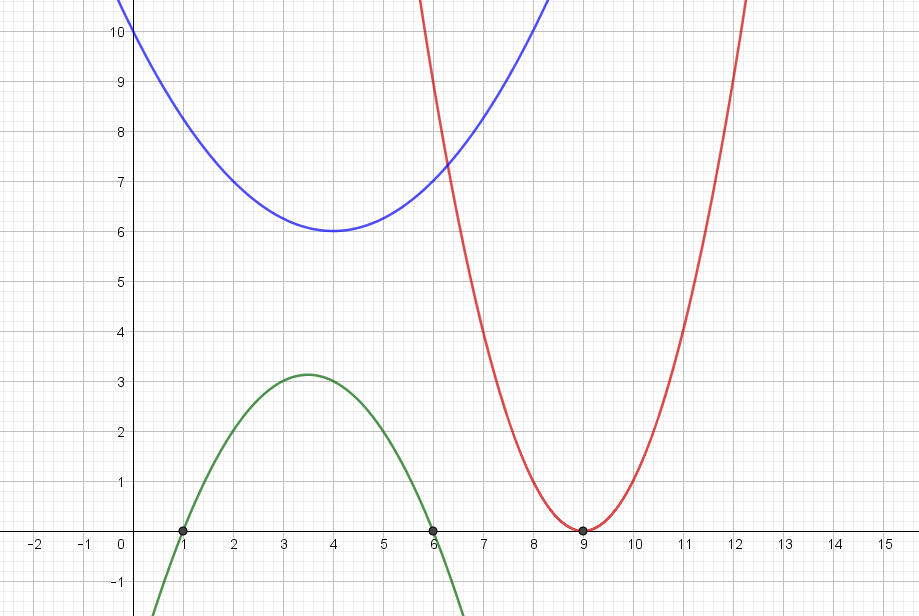
Hvis vi løser andengradsligningen \[ f(x)=ax^2 + bx + c=0 \] finder vi andengradspolynomiets rødder. Men at løse \(f(x)=0\), svarer netop til at bestemme, hvor den tilhørende parabel skærer \(x\)-aksen. I figur 1 kan vi se, at den grønne parabel skærer \(x\)-aksen to steder. Det vil sige, at det tilhørende andengradspolynomium har to rødder. Den røde parabel skærer \(x\)-aksen ét sted – det tilhørende andengradspolynomium har altså én rod. Endelig kan vi se, at den blå parabel slet ikke skærer \(x\)-aksen, og det tilhørende andengradspolynomium har derfor ingen rødder.
Du husker nok, hvordan man bestemmer antallet af rødder i et andengradspolynomium. Vi har brug for diskriminanten \(d\):
\[ d = b^2-4ac \tag{1}\]
Og der gælder så, at \[ \begin{aligned} &d<0: \quad f \text{ har ingen rødder} \\ &d=0: \quad f \text{ har én rod} \\ &d>0: \quad f \text{ har to rødder} \\ \end{aligned} \]
Idéen er nu at undersøge, om vi kan bruge kunstig intelligens til at afgøre1, om et andengradspolynomium overhovedet har nogle rødder alene ude fra de tre koefficienter \(a\), \(b\) og \(c\) – og helt uden at kende noget til diskriminantformlen i (1)!
1 Det er klart, at der er intet nyt under solen her. Vi kan jo bare selv beregne diskriminanten og svare på spørgsmålet. Men formålet er her at lære lidt om, hvad det vil sige at bruge kunstig intelligens i et tilfælde, hvor vi allerede selv kender svaret. Desuden findes der ingen lukkede løsningsformler for at bestemme rødder i et polynomium, så snart graden af polynomiet er \(5\) eller derover. Så idéen kan generaliseres, og så er den måske slet ikke så tosset endda!
Inden vi går i gang, vil vi starte med at indse, at i stedet for at løse ligningen
\[ A x^2 + Bx + C = 0, \quad \quad A \neq 0 \tag{2}\]
(hvis du undrer dig, så er det med vilje, at vi lige nu bruger store bogstaver til koefficienterne), så kan vi lige så godt løse en ligning på formen
\[ x^2 + bx +c =0 \] hvor altså \(a=1\). Det virker måske som en forsimpling, men da vi i (2) har antaget, at \(A \neq 0,\) så kan vi dividere igennem med \(A\) og få
\[ \begin{aligned} \frac{A}{A} x^2 + \frac{B}{A} x + \frac{C}{A} &= \frac{0}{A} \quad \Leftrightarrow \\ x^2 + \frac{B}{A} x + \frac{C}{A} &= 0. \end{aligned} \]
Det betyder, at når vi skal bestemme rødder i andengradspolynomier, så er det tilstrækkeligt, at betragte andengradspolynomier med en forskrift på formen
\[ f(x)=x^2+bx+c, \] hvor \(b=B/A\) og \(c=C/A\). Man kan altså bare tage sit oprindelige andengradspolynomium \(g(x)=Ax^2+Bx+C\) og dividerer igennem med \(A\). Lad os illustrere det med et eksempel.
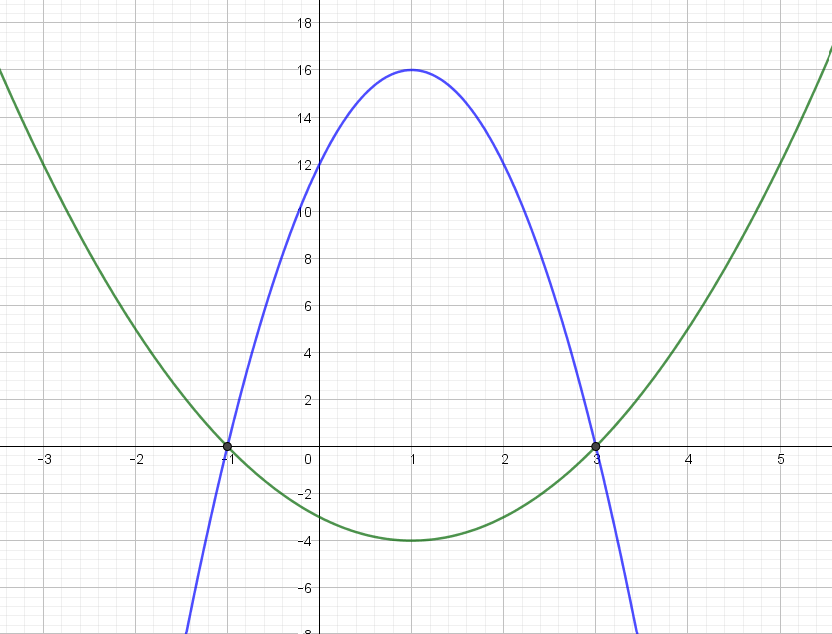
Eksempel 1 Betragt andengradspolynomiet med forskriften
\[ g(x)=-4x^2+8x+12 \] Her har vi \(A=-4, B=8\) og \(C=12\). Løser vi ligningen \(g(x)=0\), finder vi ud af, at \(g\) har to rødder nemlig \(-1\) og \(3\). Dividerer vi forskriften for \(g\) igennem med \(A=-4\) fås et nyt andengradspolynomium \(f\) med forskrift
\[ f(x)=x^2-2x-3 \] Her er koefficienterne \(a=1, b=-2\) og \(c=-3\). Men \(f\) har præcis samme rødder som \(g\) – nemlig \(-1\) og \(3\). Dette ses også illustreret i figur 2, hvor grafen for \(g\) og \(f\) begge skærer \(x\)-aksen i \(-1\) og \(3\).
Træningsdata
I dette eksempel vil vi nøjes med at se på, om vi kan bruge en metode fra kunstig intelligens, så vi forhåbentlig kan få svar på, om et givent andengradspolynomium enten har ingen eller en eller to rødder. Vi vil altså gerne finde en metode, som for en given parabel kan svare på, om parablen skærer \(x\)-aksen eller ej (og altså ikke hvor mange gange den eventuelt skærer \(x\)-aksen).
For at bruge kunstig intelligens skal vi have lavet en masse eksempler på forskellige andengradspolynomier (det vil her sige med forskellige værdier af \(b\) og \(c\)) samtidig med, at vi også finder ud af, om det tilhørende andengradspolynomium har rødder eller ej. Den værdi, der angiver om et polynomium har rødder eller ej, kalder man for en targetværdi. Man kunne for eksempel gøre det ved at sige, at hvis et andengradspolynomium har én eller to rødder, så sætter vi targetværdien til \(1\), og hvis et andengradspolynomium ikke har nogle rødder, så sætter vi targetværdien til \(-1\). Tænk på det som en lille label du sætter på hvert eksempel, hvor du fortæller, hvad det rigtige svar er – “det er altså det her, jeg gerne vil have, at du lærer!”. Samlet set kalder man de forskellige eksempler inklusiv targetværdien for træningsdata.
Træning af kunstig intelligens
En simpel metode inden for kunstig intelligens er at prøve at bestemme en ret linje, som kan bruges til at adskille de røde punkter fra de blå punkter i det punktplot, som I har lavet i opgave 3.
Hvis man skal have en computer til at gøre det, så vil man typisk starte med en hel tilfældig ret linje med en ligning på formen
\[y=a \cdot x+b\]
og så prøve at opdatere hældningen \(a\) og skæring med \(y\)-aksen \(b\), sådan at linjen bliver bedre og bedre til at adskille de røde punkter fra de blå.
Nu ser vi jo på andengradspolynomier med en forskrift på formen \(f(x)=x^2+bx+c\). Det vil sige, at \(b\) allerede har en betydning. Derfor er det ikke så hensigtsmæssigt at bruge \(b\) igen i ligningen for en ret linje. Derfor vælger vi her at beskrive den rette linje med en ligning på formen
\[ y = w_1 \cdot x + w_0 \] Det vil altså sige, at \(w_1\) er linjens hældning, og \(w_0\) er linjens skæring med \(y\)-aksen.
Som du netop har opdaget, er det en umulig opgave, vi har givet os selv! Vi kan ikke finde en ret linje, som i alle tilfælde kan bruges til at adskille de røde punkter fra de blå. 😕
Lad os se på hvorfor. Som tidligere nævnt har vores linje en ligning på formen
\[ y=w_1 \cdot x + w_0 \]
Men nu har vi \(b\)-værdier ud af \(x\)-aksen og \(c\)-værdier op af \(y\)-aksen, så i virkeligheden ser ligningen sådan her ud:
\[ c=w_1 \cdot b + w_0 \tag{3}\]
hvor \(b\) og \(c\) jo svarer til koefficinter i forskellige andengradspolymonier med forskrift \(f(x)=x^2+bx+c\).
Vi husker nu på formlen for diskriminanten \(d=b^2-4ac=b^2-4c\), da \(a=1\) i vores eksempel. Skillelinjen for om andengradspolynomiet har ingen eller flere rødder, går netop ved \(d=0\). Det vil sige
\[ b^2-4c =0 \tag{4}\]
som kan omskrives til
\[ c = \frac{1}{4}b^2 \tag{5}\]
Men vi kan ikke finde nogle værdier af \(w_0\) og \(w_1\), så udtrykket i (3) kommer til at svare til udtrykket i (5). Det er fordi, at i (3) indgår der kun et \(b\), mens der i (5) indgår et \(b^2\). Denne observation giver os imidlertid også en løsning på vores problem. I stedet for at lade træningsdata bestå af \(b\)- og \(c\)-værdier, så vil vi i stedet lade træningsdata bestå af \(b^2\)- og \(c\)-værdier! Det vil sige, at vi ud af \(x\)-aksen vil afsætte \(b^2\) og op af \(y\)-aksen, vil vi afsætte \(c.\)
Idéen med at prøve at adskille to grupper af punkter med en ret linje bruges blandt andet i den AI-metode, som kaldes for perceptroner. Metoden kan bruges, når man gerne vil kunne adskille to grupper af punkter fra hinanden baseret på en række forskellige værdier – disse værdier kalder man for features. Du kender måske kandidattests, hvor man på baggrund af svarene fra en række spørgsmål gerne vil kunne forudsige, om en person vil stemme på rød eller blå blok til det næste valg. Det kunne man for eksempel bruge en perceptron til at hjælpe med at afgøre, og det kan du læse meget mere om her.
Hvis du vil prøve at bruge den metode på dine data om andengradspolynomier, kan du gøre det her.