Sandsynlighedsregning og mængdeteori

I det følgende skal vi se på sandsynlighedsteori. Alle har selvfølgelig en fornemmelse for, hvor sandsynligt det er, at "noget" indtræffer – for eksempel at man slår en sekser med en terning eller trækker et rødt kort fra et spil kort. Hurtigt kan det dog blive mere besværligt, og for at kunne arbejde systematisk med sandsynligheder er det nødvendigt først at forstå mængdeteori, som kan være med til at give overblik over det, man i sandsynlighedsregning kalder for hændelser.

Mængdeteori

En mængde er blot en samling af forskellige elementer. Det kunne være en samling, der indeholder bogstaverne \(b\), \(d\) og \(k\). Denne mængde skrives

\[\{b,d,k\}.\]

Vi siger, at mængden indeholder elementerne \(b\), \(d\) og \(k\). Hvis vi kalder mængden for \(M\), betyder \(d\in M\), at \(M\) indeholder elementet \(d\) (eller at \(d\) er indeholdt i \(M\)). At et element \(x\) ikke er i mængden \(M\) skrives som \(x\not \in M\).

Bemærk, at en mængde kan indeholde alt muligt. Det kunne også være en mængde med tal som \(\{1,3,5\}\) eller en mængde med personer.

Hvis man har to mængder \(A\) og \(B\), da siger vi, at de to mængder er ens, hvis det er sådan, at ethvert element, der er i \(A\), også er i \(B\), og ethvert element, der er i \(B\), også er i \(A\). Hvis \(A\) og \(B\) er ens, skrives det som \(A=B\).

Eksempel 1 (Ens mængder) Vi ser på følgende tre mængder: \[ \begin{aligned} A &=\{1,2,3,5\} \\ B &=\{1,4,5\} \\ C &=\{1,3,2,5\}. \end{aligned} \] Hvilke af disse er mon ens? Her er det mængderne \(A\) og \(C\), som er ens, hvilket viser, at rækkefølgen ved opskrivningen af elementerne ikke er vigtig. Det vigtige er altså blot, om et element er med i mængden eller ej.

Delmængde

Man kalder \(A\) for en delmængde af \(B\), hvis alle de elementer, som er i \(A\), også findes i \(B\). I det tilfælde skriver man:

\[ A \subseteq B. \]

Dette er illustreret i figur 1, som kaldes for et Venn-diagram.

Figur 1: Venn-diagram som illustrerer, at \(A\) er en delmængde af \(B\): \(A\subseteq B\).

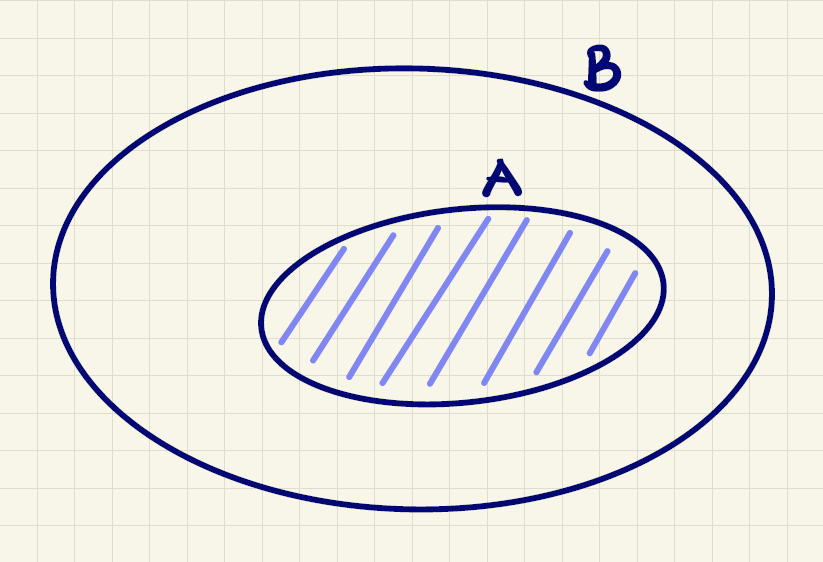
Ofte vil man arbejde med flere mængder og kombinere disse til at lave nye mængder.

Foreningsmængde og fællesmængde

Givet to mængder \(A\) og \(B\), da indføres foreningsmængden af \(A\) og \(B\) betegnet med

\[A\cup B\]

som mængden, der netop indeholder de elementer, som er i \(A\) eller \(B\) eller begge af disse. Dette er illustreret i figur 2.

Figur 2: Venn-diagram som illustrerer foreningsmængden \(A\cup B\).

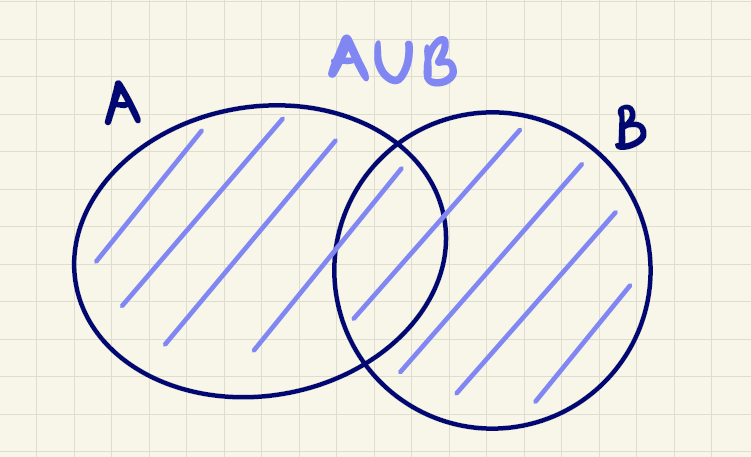
Læg mærke til, at \(A \cup B = B \cup A\).

Desuden indføres fællesmængden af \(A\) og \(B\) betegnet med

\[A\cap B\]

som mængden, der netop indeholder de elementer, som er indeholdt i både \(A\) og \(B\). Det er vist i figur 3.

Figur 3: Venn-diagram som illustrerer fællesmængden \(A\cap B\).

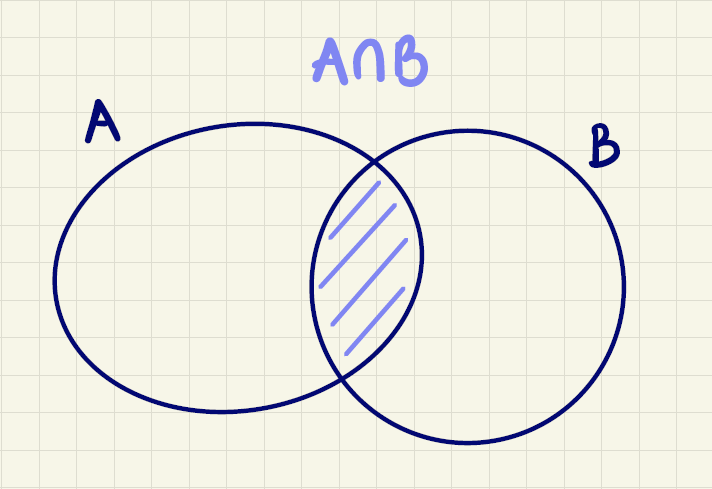
Læg mærke til, at \(A \cap B = B \cap A\).

Eksempel 2 (Foreningsmængde og fællesmængde) Vi lader

\[ A=\{1,2,3,4,5,6\} \quad \textrm{og} \quad B=\{2,4,6,8\}. \] Foreningsmængden er da

\[ A\cup B=\{1,2,3,4,5,6,8\} \] og fællesmængden er

\[ A\cap B=\{2,4,6\}. \]

Disjunkte mængder

En vigtig mængde er den tomme mængde, som betegnes med \(\emptyset\). Det er altså mængden uden elementer.

Hvis to mængder \(A\) og \(B\) opfylder, at \(A\cap B=\emptyset\) siger man, at \(A\) og \(B\) er disjunkte. Disjunkte mængder har derved ikke nogle elementer til fælles. Man kan også sige, at der ikke er noget overlap mellem de to mængder. Et eksempel på to disjunkte mængder er vist i figur 4. Her ses det tydeligt, at de to mængder ikke overlapper.

Figur 4: Venn-diagram som illustrerer to disjunkte mængder \(A\) og \(B\).

Eksempel 3 (Disjunkte mængder) Vi ser på følgende tre mængder:

\[ \begin{aligned} A &=\{1,2,3,5\} \\ B &=\{1,4,6\} \\ C &=\{3,5,7\}. \end{aligned} \] Her er

\[ \begin{aligned} A \cap B &= \{1\} \\ A \cap C &= \{3, 5\} \\ B \cap C &= \emptyset. \end{aligned} \] Det vil sige, at \(B\) og \(C\) er disjunkte.

Komplementærmængde

Når man betragter mængder, vil man ofte udelukkende se på elementer af en bestemt slags. Som i de tidligere eksempler kunne det være, at alle elementer er heltal. Her tænker vi, at vi arbejder indenfor et univers \(U\), som er alle mulige tænkelige elementer, og de mængder vi ellers ser på indeholder så elementer, som er i mængden \(U\).

Lad os se på et univers \(U\) og en mængde \(A\), som kun indeholder elementer, der også er i \(U\). Vi vil så indføre komplementærmængden for \(A\), som mængden indeholdende netop de elementer fra \(U\), som ikke er i \(A\). Komplementærmængden til \(A\) skrives \(\overline{A}\). Dette er illustreret i figur 5.

Figur 5: Venn-diagram som illustrerer komplementærmængden \(\overline{A}\).

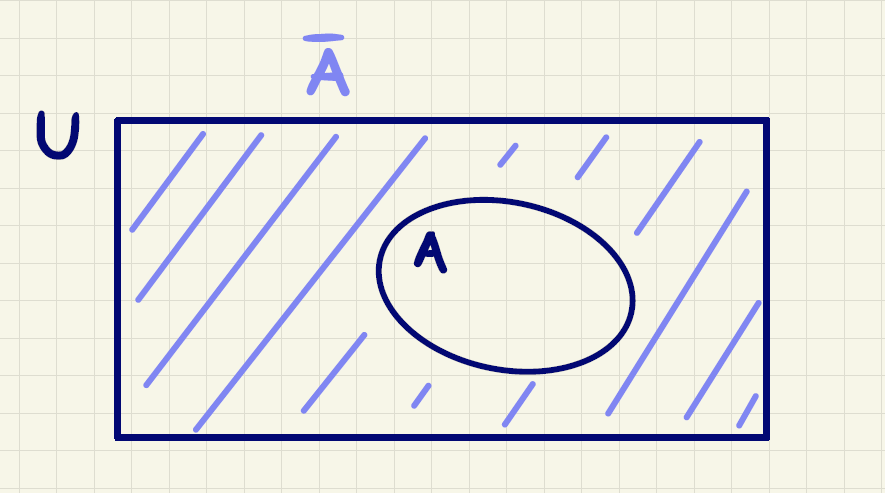
Lad os se på et eksempel.

Eksempel 4 (Komplementærmængde) Vi ser på et univers

\[ U=\{1,2,3,4,5,6,7,8\} \]

og en mængde \(A\):

\[ A=\{1,2,3\}. \]

Da er komplementærmængden til \(A\):

\[ \overline{A}= \{4,5,6,7,8\} \]

fordi det netop er alle de elementer i universet \(U\), som ikke er i \(A\).

Givet en mængde \(A\), så kaldes \(A_1,A_2,...,A_n\) en opdeling af \(A\), hvis \(A_1,A_2,...,A_n\) er mængder, som er parvis disjunkte, og hvor

\[ A=A_1\cup A_2\cup \cdots \cup A_n. \]

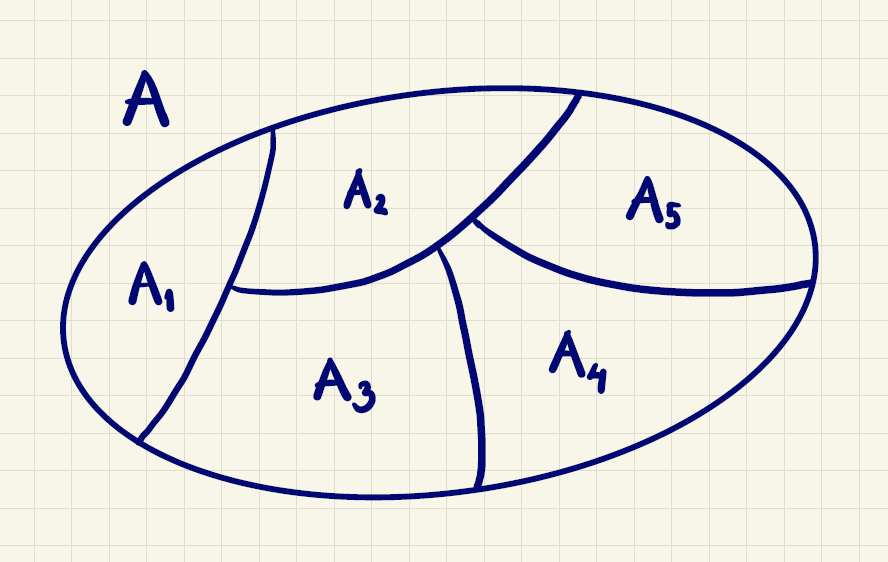
Et eksempel på en opdeling af en mængde \(A\) i mængderne \(A_1, A_2, A_3, A_4\) og \(A_5\) ses i figur 6.

Figur 6: Venn-diagram som illustrerer en opdeling af en mængde \(A\) i mængderne \(A_1, A_2, A_3, A_4\) og \(A_5\).

Eksempel 5 (Opdeling) Hvis man har mængden

\[ A=\{1,2,3,4,5,6,7,8\} \]

kan man lave en opdeling af \(A\) i to mængder \(A_1\) og \(A_2\), hvor \(A_1\) indeholder de lige tal fra \(A\), mens \(A_2\) indeholder de ulige tal fra \(A\):

\[ \begin{aligned} A_1 &= \{2, 4, 6, 8\} \\ A_2 &= \{1, 3, 5, 7\}. \end{aligned} \]

Hvis det var en mængde indeholdende elever på et gymnasium, kunne man lave en opdeling efter hvilke klasser, man kommer fra.

Sandsynlighed

I sandsynlighedsregning tænker man, at man udfører et forsøg eller et eksperiment, hvor der er nogle mulige udfald. Mængden af disse udfald kaldes udfaldsrummet.

På forhånd ved man ikke, hvad resultatet af et eksperiment bliver, men ofte kender man sandsynligheden for, at hvert udfald i et udfaldsrum \(U\) indtræffer. Rent matematisk svarer det til, at man kender en såkaldt sandsynlighedsfunktion \(P\).

Formelt definerer man et sandsynlighedsfelt på denne måde:

Definition 1 (Sandsynlighedsfunktion) Ved et sandsynlighedsfelt forstås en sandsynlighedsfunktion \(P\), der til hvert udfald \(u_i\) i et udfaldsrum \(U=\{u_1,u_2,\ldots,u_n\}\) knytter et reelt tal \(P(u_i)\), hvor

\[0 \leq P(u_i)\leq 1\]

og hvor

\[ P(u_1)+P(u_2)+\cdots + P(u_n)=1=100 \%. \]

\(P(u_i)\) kaldes sandsynligheden for udfaldet \(u_i\).

Lad os se på et konkret eksempel.

Eksempel 6 (Sandsynlighedsfunktion) Vi tænker, at man slår med en almindelig terning, hvor udfaldet kan være \(1,2,3,4,5,6\). Udfaldsrummet er altså \(U= \{1,2,3,4,5,6\}.\)

Her vil sandsynligheden for, at man slår \(3\) være \(P(3)=\frac{1}{6}\). Ved dette eksempel er sandsynligheden for hvert udfald ens. Sandsynlighedsfeltet kan skrives op på denne måde:

\(u\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
\(P(u)\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)

Når vi i eksemplet ovenfor siger, at sandsynligheden for at slå \(1,2,3,4,5\) eller \(6\) alle er \(\frac{1}{6}\), så er det baseret på vores fornuft: Terningen har seks sider, og der må være samme sandsynlighed for at lande på hver af dem¹ – ergo er hver af sandsynlighederne \(\frac{1}{6}\). En sandsynlighed bestemt på denne måde, kaldes for en a priori sandsynlighed.

¹ Hvis der altså er tale om en såkaldt ærlig terning. Man kan også købe "snydeterninger", som meget gerne vil lande på for eksempel 6. De er gode at have med til pakkespil (hvis altså dine medspillere bruger almindelige terninger)!

Hændelse

En delmængde \(A\) af udfaldsrummet \(U\) kaldes for en hændelse:

Definition 2 (Hændelse) Lad \(U\) være et udfaldsrum. En delmængde \(A\) af udfaldsrummet kaldes for en hændelse.

Vi definerer sandsynligheden for \(A\) ved

\[ P(A) = \sum_{u\in A} P(u). \tag{1}\]

Sandsynligheden for en hændelse fås altså ved at lægge sandsynligheden for hver af de udfald, som udgør hændelsen, sammen. Det illustreres nemmest med et eksempel:

Eksempel 7 (Lige antal øjne) Lad os igen se på sandsynlighedsfeltet i eksempel 6. Et eksempel på en hændelse er, at terningen viser et lige antal øjne. Det vil sige, at

\[ A= \{2, 4, 6\}. \]

Dermed er

\[ P(A) = \sum_{u\in A} P(u) = P(2) + P(4) + P(6) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2} \] som forventet.

Symmetriske sandsynlighedsfelter

Hvis sandsynligheden for hvert udfald er den samme kaldes sandsynlighedsfeltet for symmetrisk. Det vil sige, at sandsynlighedsfeltet i eksempel 6 er symmetrisk. Hvis der i alt er \(n\) udfald, vil sandsynligheden for et enkelt udfald \(u\in U\) i et symmetrisk sandsynlighedsfelt være

\[ P(u)=\frac{1}{n}. \]

Vi ser nu på en hændelse \(A\), som i alt består af \(k\) udfald. Da bliver sandsynligheden for \(A\)

\[ P(A)=\underbrace{\frac{1}{n} + \frac{1}{n} + \cdots + \frac{1}{n}}_{k \textrm{ led}}= \frac{k}{n}. \] De udfald, som er i hændelsen \(A\), kalder man også for gunstige udfald. Det betyder, at ovenstående formel kan udtrykkes på denne måde:

\[ P(A)=\frac{\textrm{antal gunstige udfald}}{\textrm{antal mulige udfald}}. \] Vær opmærksom på, at denne formel kun gælder i symmetriske sandsynlighedsfelter.

Eksempel 8 (Lige antal øjne, fortsat) Da sandsynlighedsfeltet, som vi så på i eksempel 6 og eksempel 7 er symmetrisk, kunne vi også have fundet \(P(A)\) ved at bruge formlen ovenfor. Der er \(3\) udfald i \(A\) og \(6\) mulige udfald i alt. Dermed er

\[ P(A)=\frac{3}{6}=\frac{1}{2}. \]

Ikke-symmetriske sandsynlighedsfelter

Det er selvfølgelig ikke altid, at man har et symmetrisk sandsynlighedfelt. Vi vil illustrere et ikke-symmetrisk sandsynlighedsfelt med et eksempel.

Eksempel 9 (Produktion af bolde) Vi forestiller os en maskine, der producerer bolde og for hver gang, der bliver lavet en bold, er der \(20 \%\) chance for, at den bliver rød, \(40 \%\) chance for at den bliver blå, \(10 \%\) chance for at den bliver grøn, og \(30 \%\) chance for at den bliver gul.

Her er udfaldsrummet \(U = \{\textrm{rød}, \textrm{blå}, \textrm{grøn}, \textrm{gul} \}\). Desuden er \(P(\textrm{rød})=20 \%\), \(P(\textrm{blå})=40 \%\), \(P(\textrm{grøn})=10 \%\) og \(P(\textrm{gul})=30 \%\). Opskrevet i en tabel ser det sådan her ud:

\(u\)	rød	blå	grøn	gul
\(P(u)\)	\(20 \%\)	\(40 \%\)	\(10 \%\)	\(30 \%\)

Hvis vi ser på hændelsen

\[ A: \textrm{der laves en rød eller blå bold}, \]

da bliver sandsynligheden ifølge definition 2:

\[ P(A)=P(\textrm{rød})+P(\textrm{blå})=20\%+40\%=60\%. \]

Altså blot summen af sandsynlighederne for hvert af udfaldene i hændelsen.

Hvis man ser på hændelser som mængder, kan man ved hjælp af Venn-diagrammet i figur 7 se, at der må gælde

\[ P(A\cup B)=P(A)+P(B)-P(A\cap B). \]

Figur 7: Venn-diagram som illustrerer sammenhængen mellem \(P(A\cup B)\), \(P(A)\), \(P(B)\) og \(P(A\cap B)\).

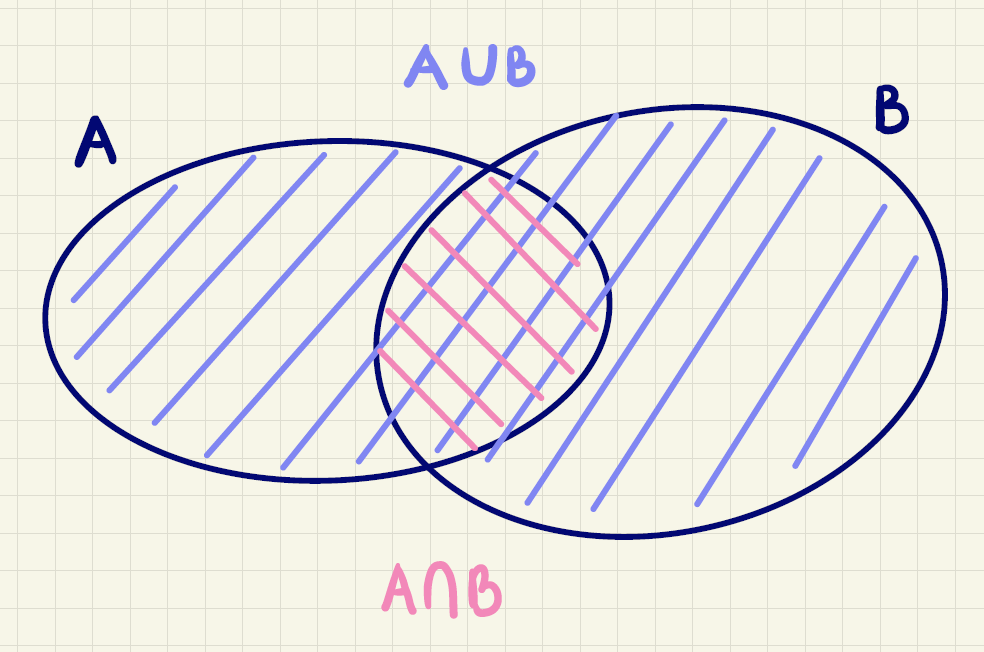
Vi kan argumentere for resultatet på følgende måde: Hvis man tager alle udfald fra \(A\) og bagefter alle udfald fra \(B\), vil de udfald, som er i begge hændelser (svarende til fællesmængden \(A \cap B\)), blive taget med to gange. Hvis vi vil finde sandsynligheden for \(P(A \cup B)\), er vi derfor nødt til at trække sandsynligheden \(P(A \cap B)\) fra \(P(A)+P(B)\), fordi den er talt med to gange.

Hvis de to hændelser \(A\) og \(B\) er disjunkte, hvorved \(A\cap B\) er den tomme mængde, bliver

\[ P(A\cup B)=P(A)+P(B). \]

Når man ser på hændelsen \(\overline{A}\) svarende til komplementærmængden af en hændelse \(A,\) er det oplagt, at

\[ P(\overline{A}) + P(A)=1 \] og dermed må

\[ P(\overline{A})=1-P(A). \]

Eksempel 10 (Kast med to terninger) Vi kaster en ganske almindelig terning to gange og ønsker at finde sandsynligheden for, at man mindst en af gangene får en 6’er. Vi definerer hændelserne:

\[ \begin{aligned} &A: \textrm{man slår en 6'er i det første kast} \\ &B: \textrm{man slår en 6'er i det andet kast} \\ \end{aligned} \] hvor der her er underforstået, at det er lige meget, hvad man slår i det modsatte kast.

Da er den ønskede sandsynlighed:

\[ P(A\cup B)=P(A)+P(B)-P(A\cap B). \] Her må

\[ P(A)=P(B)=\frac{1}{6} \]

og

\[ P(A\cap B)=\frac{1}{36} \]

da \(A\cap B\) må svare til, at man får en 6’er i begge kast.

Derfor er

\[ P(A\cup B)=P(A)+P(B)-P(A\cap B)=\frac{1}{6}+\frac{1}{6}-\frac{1}{36}=\frac{11}{36}. \] Læg her mærke til, at udfaldet, hvor man i begge kast får en 6’er, både er i hændelsen \(A\) og \(B\).

Estimat for sandsynlighed

Ofte vil man støde på tilfælde, hvor man ikke kender en sandsynlighed, og heller ikke bare kan regne sandsynligheden ud. Det kunne for eksempel være sandsynligheden for at vinde i et lykkehjul eller i et reklamespil. Her vil firmaer ofte få det til at fremstå som om, at det er let at vinde et større beløb ved, at alle felter er lige store. Det er illustreret i figuren herunder:

Figur 8: Lykkehjul.

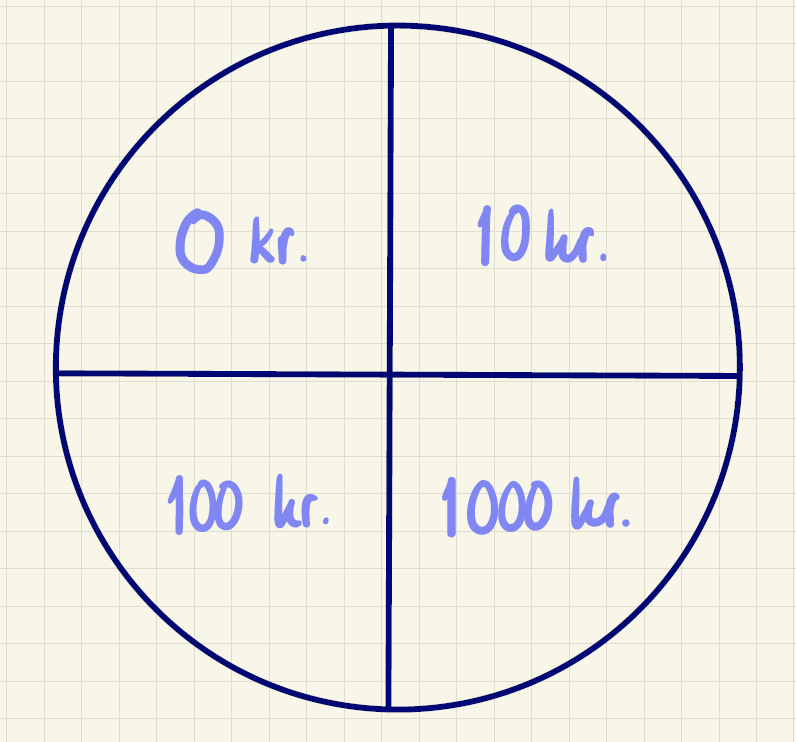
Her skulle man tro, at man vinder 1000 kroner med sandsynlighed \(\frac{1}{4}\), men det er desværre nok ikke tilfældet.

For at få et estimat for sandsynligheden for at vinde, kan man prøve lykkehjulet mange gange og finde et estimat, \(\hat{p}\), for sandsynligheden for at vinde ved at udregne

\[ \hat{p}=\frac{\textrm{antal successer}}{\textrm{antal forsøg}}. \]

Her har vi antaget, at sandsynligheden for succes ikke ændres. Estimatet for sandsynligheden fås altså ved at tage en stikprøve, hvor man prøver mange gange. En sandsynlighed bestemt på denne måde kaldes for en frekventiel sandsynlighed.

Eksempel 11 (Uærlig terning) En klasse slår med en uærlig terning 234 gange og noterer det antal øjne, terningen viser. På den baggrund kan de estimere sandsynligheden for henholdsvis \(1, 2, 3, 4, 5\) og \(6\):

\(u\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
Antal successer	\(10\)	\(13\)	\(19\)	\(19\)	\(30\)	\(143\)
\(P(u)\)	\(\frac{10}{234} \approx\) \(4.3 \%\)	\(\frac{13}{234} \approx\) \(5.6 \%\)	\(\frac{19}{234} \approx\) \(8.1 \%\)	\(\frac{19}{234} \approx\) \(8.1\%\)	\(\frac{30}{234} \approx\) \(12.8 \%\)	\(\frac{143}{234} \approx\) \(61.1 \%\)

Her kan man jo tydeligt se, hvorfor det er en god terning at snige med til et pakkespil!

Betinget sandsynlighed og uafhængighed

Nogle gange kan man være interesseret i sandsynligheden for, at en hændelse \(A\) indtræffer, når man allerede ved, at en anden hændelse \(B\) er indtruffet. Det kunne for eksempel være sandsynligheden for at få 12 til skriftlig eksamen i matematik, hvis man allerede ved, at eleven går i en naturvidenskabelig studieretning.

Til en sådan sandsynlighed benyttes notationen \(P(A|B)\). Det er altså sandsynligheden for, at \(A\) sker, når det er givet, at \(B\) er sket. Det læses derfor også som sandsynligheden for \(A\) givet \(B\).

Lad os se på et par eksempler:

Eksempel 12 (Kast med en ærlig terning) Vi ser igen på, at man slår med en ganske almindelig terning. Her ønsker vi at bestemme sandsynligheden for, at man slår noget lige givet, at man slår mindst \(4\).

Her vil

\[ A=\{2,4,6\} \]

svarer til at slå noget lige og

\[ B=\{4,5,6\} \]

svarer til at slå mindst \(4\). Det er så netop sandsynligheden \(P(A|B)\) vi skal have fundet.

Her kan vi tænke på det som om, at udfaldrummet kun består af \(B=\{4,5,6\}\) og ved hændelsen \(A\), skal vi kun se på den del, som også er i \(B\). Det svarer til

\[ A \cap B = \{4, 6\}. \]

Da det samtidigt er et symmetrisk sandsynlighedsfelt, vil vi få sandsynligheden ved

\[ P(A|B)=\frac{\textrm{antal gunstige}}{\textrm{antal mulige}}=\frac{2}{3}. \]

I formlen i ovenstående eksempel kan vi prøve at dele med det samlede antal udfald i tæller og nævner:

\[ P(A|B)=\frac{\frac{2}{6}}{\frac{3}{6}}. \]

I tælleren ser vi faktisk på sandsynlighden for fællesmængden for de to hændelser:

\[ P(A\cap B)=\frac{2}{6} \]

mens nævneren svarer til

\[ P(B)=\frac{3}{6}. \]

Det leder frem til følgende definition på betinget sandsynlighed

Definition 3 (Betinget sandsynlighed) Lad \(A\) og \(B\) være to hændelser, hvor \(P(B) \neq 0\). Ved den betingede sandsynlighed \(P(A | B)\) forstås tallet

\[ P(A|B)=\frac{P(A\cap B)}{P(B)} \]

Lad os se på endnu et eksempel.

Eksempel 13 (Interesse for fodbold) Her udvælger vi en tilfældig gymnasieelev og ser på, om den udvalgte er interesseret i fodbold. Her kan vi for eksempel se på sandsynligheden for, at den udvalgte er interesseret i fodbold givet, at den udvalgte er en dreng.

Alle vil nok tænke, at information om kønnet af den udvalgte vil ændre sandsynligheden for, om den udvalgte er interesseret i fodbold.

Lad os sige, at der i alt er \(500\) gymnasieelever, hvoraf \(200\) er drenge og \(300\) piger. Desuden er \(120\) drenge interesseret i fodbold, mens \(90\) piger er interesseret i fodbold.

Vi kan nu beregne \(P(\textrm{fodbold})\), \(P(\textrm{fodbold } | \textrm{ dreng})\) og \(P(\textrm{fodbold } | \textrm{ pige})\).

Vi antager, at hver gymnasieelev udvælges med samme sandsynlighed. Der er altså tale om et symmetrisk sandsynlighedsfelt. Derfor er

\[ P(\textrm{fodbold})=\frac{\textrm{antal gunstige}}{\textrm{antal mulige}}=\frac{210}{500}=42\%. \]

Hvis vi skal finde \(P(\textrm{fodbold }| \textrm{ dreng})\) er det sandsynligheden for, at den udvalgte er interesseret i fodbold givet, at den udvalgte er en dreng. Med denne formulering giver det mening kun at se på drengene, og om en udvalgt blandt drengene vil være interesseret i fodbold:

\[ P(\textrm{fodbold }| \textrm{ dreng})=\frac{\textrm{antal gunstige}}{\textrm{antal mulige}}=\frac{120}{200}=60\%. \]

Her ses det, at hvis man får information om, at det er en dreng, der er udvalgt, så ændrer det på sandsynligheden for, at den udvalgte er interesseret i fodbold.

Ved beregningen af \(P(\textrm{fodbold }| \textrm{ dreng})\) i eksemplet ovenfor kan vi igen dividere i tæller og nævner med antallet af gymnasieelever i alt og få:

\[ P(\textrm{fodbold }| \textrm{ dreng})=\frac{\frac{120}{500}}{\frac{200}{500}}. \]

Her svarer tælleren til, at den udvalgte både er en dreng, og at han er interesseret i fodbold (hændelsen svarer altså til en fællesmængde). Nævneren svarer til sandsynligheden for, at den udvalgte er en dreng. Altså

\[ P(\textrm{fodbold }| \textrm{ dreng})=\frac{P(\textrm{fodbold} \cap \textrm{dreng})}{P(\textrm{dreng})}. \]

Læg mærke til, at det igen svarer til definition 3. Beregningen med formlen svarer til, at man begrænser sig til udfald, hvor \(B\) indtræffer, og ser hvor sandsynligt det er, at \(A\) indtræffer der.

Fra definition 3 er det nemt at udlede følgende sætning:

Sætning 1 Lad \(A\) og \(B\) være to hændelser, da gælder

\[ P(A\cap B)= P(A|B)\cdot P(B) \]

Man siger to hændelser er uafhængige, hvis viden om, at den ene hændelse indtræffer, ikke påvirker sandsynligheden for den anden. Det kan vi formulere sådan her:

Definition 4 (Uafhængige hændelser) Lad \(A\) og \(B\) være to hændelser. Da siger man, at \(A\) og \(B\) er uafhængige, hvis

\[ P(A|B)=P(A) \]

I eksempel 13 er der ikke uafhængighed mellem hændelserne at "den udvalgte er en dreng" og hændelsen "den udvalgte er interesseret i fodbold". I eksemplet var \(P(\textrm{ fodbold})=42\%\), mens \(P(\textrm{ fodbold } | \textrm{ dreng})=60\%\).

Et af de helt centrale resultater i forbindelse med betingede sandsynligheder er Bayes sætning.

Sætning 2 (Bayes sætning) Givet to hændelser \(A\) og \(B\). Da gælder, at

\[P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}\]

Bevis

Givet to mængder \(A\) og \(B\), så ved vi, at \(A\cap B=B\cap A\), og derfor er

\[ P(A\cap B)=P(B\cap A). \]

Vi benytter sætning 1 på begge sider af lighedstegnet og får:

\[P(A|B) \cdot P(B) = P(B|A) \cdot P(A).\]

Her isoleres \(P(A|B)\) ved at dividere med \(P(B)\):

\[ P(A|B) = \frac{P(B|A)\cdot P(A)}{P(B)}. \]

Ofte benyttes Bayes sætning til at bestemme den betingede sandsynlighed \(P(A|B)\) ud fra den betingede sandsynlighed \(P(B|A)\).

Eksempel 14 (Interesse for fodbold, fortsat) Vi ønsker at finde sandsynligheden for, at en udvalgt er en dreng givet, at den udvalgte er en, som er interesseret i fodbold. Vi vil altså bestemme sandsynligheden \(P(\textrm{dreng }| \textrm{ fodbold})\). Fra bayes sætning får vi

\[ P(\textrm{dreng }| \textrm{ fodbold})=\frac{P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{dreng})}{P(\textrm{fodbold})}. \] I eksempel 13 har vi udregnet \(P(\textrm{fodbold}) = 42 \%\) og \(P(\textrm{fodbold } | \textrm{ dreng}) = 60 \%\). Da der er \(200\) drenge ud af i alt \(500\) gymnasieelever, er \(P(\textrm{dreng}) = 40 \%\), og vi kender derfor alle sandsynligheder på højre side i ovenstående udtryk og får

\[ P(\textrm{dreng } | \textrm{ fodbold})=\frac{60 \% \cdot 40 \%}{42\%}\approx 57.1\%. \] I eksemplet var der altså \(40 \%\), som var drenge, men der var samtidig en større del af dem, som var interesseret i fodbold i forhold til pigerne. Derfor er det forventet, at den udregnede sandsynlighed er større end \(40 \%\).

Opgave: Betinget sandsynlighed og uafhængighed

Du finder en opgave om betinget sandsynlighed og uafhængighed her: Opgave 1.

Opdeling og sandsynlighed

Fra definition 2 følger det, at hvis \(A_1,A_2,...,A_n\) er en opdeling af en hændelse \(A\), så er

\[ P(A)=P(A_1)+P(A_2)+\cdots+P(A_n). \]

Når vi skal finde sandsynligheden for en hændelse \(B\), kan det nogle gange være en idé at benytte en opdeling af udfaldsrummet \(U\).

Sætning 3 (Loven om total sandsynlighed) Lad \(B\) være en hændelse og lad \(A_1,A_2,...,A_n\) være en opdeling af udfaldsrummet \(U\). Så er

\[ P(B)=P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+\cdots +P(B|A_n)\cdot P(A_n) \]

Bevis

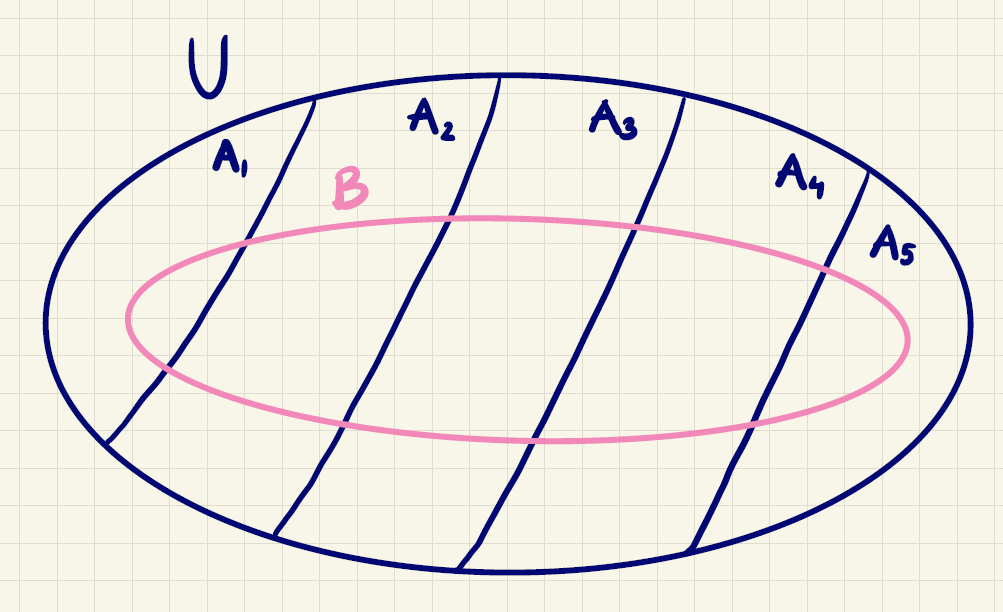
På figur 9 herunder ses det, at mængden \(B\) kan opdeles i mængderne

\[ B\cap A_1,B\cap A_2,\ldots,B\cap A_n. \]

Derfor er

\[ P(B)=P(B\cap A_1)+P(B\cap A_2)+\cdots+P(B\cap A_n). \]

Ved at benytte sætning 1 for hvert led på højresiden, får vi derfor, at

\[ \begin{aligned} P(B)=P(B|A_1)\cdot P(A_1) &+P(B|A_2)\cdot P(A_2) \\ &+\cdots +P(B|A_n)\cdot P(A_n) \end{aligned} \]

Hvilket netop var det, vi gerne ville vise.

Figur 9: En opdeling af mængden \(B\).

Vi illustrerer sætningen med eksemplet om fodbold.

Eksempel 15 (Interesse for fodbold, fortsat 2) Lad os tage eksemplet fra tidligere med fodbold, men hvor vi lige glemmer antallet af elever. Vi husker blot, at

\[ \begin{aligned} P(\textrm{dreng}) &= 40 \% \\ P(\textrm{pige}) &= 60 \% \end{aligned} \]

Samtidig ved vi, at \(60\%\) af drengene er interesseret i fodbold, og \(30\%\) af pigerne er interesseret i fodbold. Det vil sige, at

\[ \begin{aligned} P(\textrm{fodbold } | \textrm{ dreng}) &= 60 \% \\ P(\textrm{fodbold } | \textrm{ pige}) &= 30 \% \end{aligned} \]

Hvis man ønsker at beregne sandsynligheden for, at en tilfældig udvalgt gymnasieelev er interesseret i fodbold, kan vi lave en opdeling af alle gymnasieeleverne i henholdsvis drenge og piger. Fra sætning 3 får vi derfor

\[ \begin{aligned} P(\textrm{fodbold}) &=P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{dreng})+P(\textrm{fodbold } | \textrm{ pige})\cdot P(\textrm{pige}) \\ &=60\%\cdot 40\%+30\% \cdot 60 \%=42\%. \end{aligned} \]

Fra sætning 1 ved vi, at

\[ P(\textrm{fodbold} \cap \textrm{dreng}) = P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{ dreng}) \]

og vi har lige set, at

\[ \begin{aligned} P(\textrm{fodbold}) =P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{dreng})+P(\textrm{fodbold } | \textrm{ pige})\cdot P(\textrm{pige}) \end{aligned} \]

Fra definitionen på betinget sandsynlighed (definition 3) ved vi, at

\[ P(\textrm{dreng } | \textrm{ fodbold}) = \frac{P(\textrm{fodbold} \cap \textrm{dreng})}{P(\textrm{fodbold})} \]

Derfor får vi, at

\[ \begin{aligned} P(\textrm{dreng } | \textrm{ fodbold}) &=\frac{P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{ dreng})}{P(\textrm{fodbold } | \textrm{ dreng})\cdot P(\textrm{dreng})+P(\textrm{fodbold }| \textrm{ pige})\cdot P(\textrm{pige})} \end{aligned} \]

Indsætter vi de faktiske tal, får vi

\[ P(\textrm{dreng } | \textrm{ fodbold}) = \frac{60 \% \cdot 40 \%}{60 \% \cdot 40 \% + 30 \% \cdot 60 \%} \approx 57.1 \% \] hvilket stemmer med det, vi fik i eksempel 14. Bemærk, at vi her har udregnet den betingede sandsynlighed \(P(\textrm{dreng } | \textrm{ fodbold})\) uden at kende det faktiske antal elever. Det er nok at kende de procenter, som vi startede med i eksemplet.

Opgave: Opdeling og sandsynlighed

Du finder en opgave om opdeling og sandsynlighed her: Opgave 2.