Hvilken politiker er du mest enig med?

C-niveau
Kort
Samfundsfag

Forløbet kræver kendskab til:

  • Afstand mellem to punkter.

Tidsforbrug: Ca. 2 x 90 minutter.

Formål

Evnen til at skelne mellem forskellige kategorier er helt central for os som mennesker. Vi kan langt oftest kende forskel på et æble og en pære, på en cykel og en knallert eller på om en person er en kvinde eller en mand. Men hvordan får man en computer til at gøre det samme?

Formålet med dette forløb er at lære lidt om nogle af de metoder, som ligger bag, når en computer skal lære at kende forskel på forskellige ting. Forløbet slutter med at undersøge, hvordan en computer kan afgøre, hvor enig eller uenig man er med en given politiker.

Introduktion

Vi har apps på vores telefoner eller computere, som ud fra et billede kan genkende personer eller fra nogle få strofer kan genkende en sang. Der er scannere i lufthavne og andre steder, som kan genkende farlige ting, og biler har autopiloter, der selv holder afstanden til forankørende. Vi har også apps, som går den anden vej, og forvrænger et billede af en person, så personen bliver svær at genkende, men ofte alligevel kan genkendes, selvom ansigtet er fordrejet.

Så alle steder og hele tiden foregår der bevist eller ubevist en skelnen mellem forskellige kategorier, men hvordan foregår denne skelnen i grunden? Hvis vi skulle svare fyldestgørende på dette spørgsmål, om overhovedet muligt, ville det nok betyde et langt studie på universitetet og sikkert mere end dette, men lad os starte med et meget simpelt eksempel, og tage den derfra.

Vi får brug for din viden om afstande mellem punkter, men kommer også til senere at se på andre former for afstande. Det er en fordel af lave opgaverne i grupper, da der kan blive en del af diskutere.

VIDEO: Hvem ligner du mest?

I denne video gives en kort introduktion til forløbet.

Afstand mellem to punkter

NoteOpgave 1

På figur 1 nedenfor er der \(10\) røde punkter, \(10\) blå punkter og \(10\) grønne punkter – samt et enkelt gråt punkt \(P\) i midten. Et af de blå punkter er særligt markeret, men da det ligger ret langt fra \(P\) bør det nok ikke betyde så meget for, hvilket farve \(P\) skal have, som de punkter, der ligger tættere på \(P\).

  • Vurdér ud fra de øvrige punkter i nærheden af \(P\), om du synes, at \(P\) bør være rødt, blåt eller grønt, så det ligner sine naboer mest.
Figur 1: Koordinatsystem med \(10\) røde punkter, \(10\) blå punkter og \(10\) grønne punkter – samt et enkelt gråt punkt \(P\).
NoteOpgave 2

På figur 2 er der andre \(31\) punkter, samt en cirkel med radius \(10\) omkring det grå punkt \(P(15,15)\).

  • Tæl hvor mange røde, blå og grønne punkter, der ligger inde i cirklen.
  • Kan det bruges til at beslutte, hvilken farve det grå punkt bør have?
Figur 2: Koordinatsystem med \(31\) punkter, samt en cirkel med radius \(10\) omkring det grå punkt \(P(15,15)\)
NoteOpgave 3

Vi arbejder videre med punkterne fra opgave 2. Brug den interaktive figur nedenfor.

  • Hvilket resultat giver det, hvis cirklens radius kun var halvt så stor?
NoteOpgave 4

Det går nok ikke i længden blot at ville vurdere på øjemål, så du må til at regne lidt. I tabellen herunder er koordinater og farver på de \(10\) punkter, der ligger tættest på det grå punkt i opgave 2 og 3.

  • Udregn afstanden fra det grå punkt \(P(15,15)\) til hver af disse \(10\) punkter.

  • Afgør så, hvor mange af hver farve, der ligger indenfor en cirkel med radius \(5\) omkring det grå punkt. Det er nok specielt det blå punkt lige på kanten af cirklen, hvor beregningen er vigtig, men hvis en computer skal lave arbejdet automatisk, vil den jo beregne alle afstandene, da den ikke bare kan "kigge på figuren", som et menneske kan.

  • Hvilken farve tyder det på, at det grå punkt bør have?

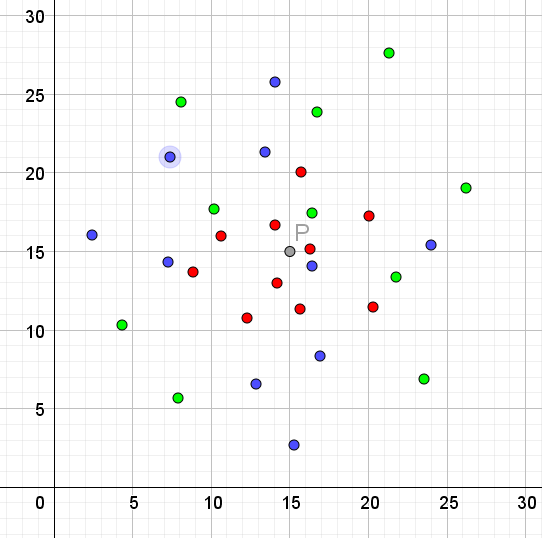
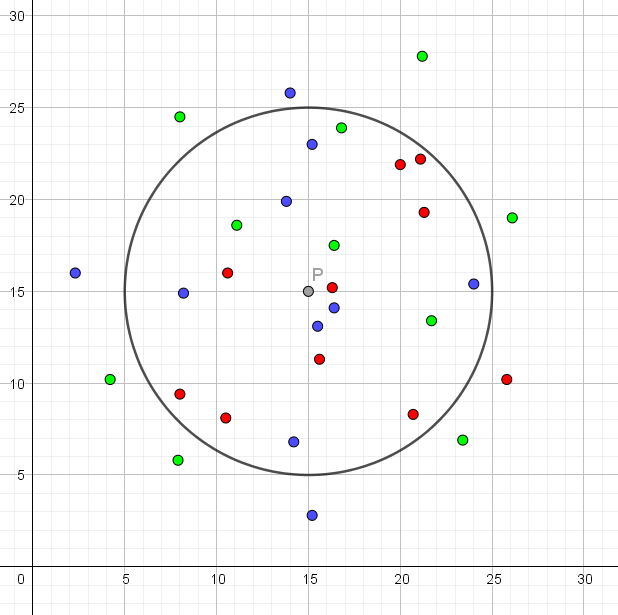
Farve
Blå \((13.8, 19.9)\) \((8.2, 14.9)\) \((16.4, 14.1)\) \((15.5, 13.1)\)
Rød \((10.6, 16.0)\) \((16.3, 15.2)\) \((15.6, 11.3)\)
Grøn \((11.1, 18.6)\) \((16.4, 17.5)\) \((21.7, 13.4)\)
NoteOpgave 5
  • Overvej, hvad der sker, hvis cirklens radius vælges som en meget lille værdi eller som en meget stor værdi i forhold til at bruge metoden til at bestemme, hvilken farve det grå punkt bør have. Kan det give problemer?
NoteOpgave 6

I den interaktive figur herunder er \(27\) andre punkter indsat i et koordinatsystem, og der er tegnet en cirkel med centrum i det grå punkt \(P(15,15)\).

  • Undersøg, hivlken farve \(P\) skal have ved forskellig valg af radius.

Opsamling

Det bliver nok klart, at der er brug for en metode til at beslutte, hvor stor radius skal være for at få det bedste resultat. Kort og lidt simpelt forklaret, involverer det noget, som man kalder træningsdata og testdata. Man har for eksempel 1000 punkter, som man kender farven på. Man lader så som om, at man ikke kender farven på for eksempel 200 af punkterne (som man så kalder testdata). Så bruger man de øvrige 800 punkter (træningsdata) til at forudsige farven af hver af de 200 punkter i testdata. Dette gør man for forskellige værdier af radius, hvorefter man vælger den radius, der forudsiger flest af de 200 punkters farve korrekt. Hvis for eksempel radius 5 forudsiger 121 punkters farve korrekt, radius 10 furudsiger 135 punkters farve korrekt, og radius 20 kun forudsiger 87 punkters farve korrekt, så har radius 10 jo klaret sig bedst.

Manhattan-afstand

I nogle situationer giver den almindelige afstand mellem punkter ikke så god mening. For eksempel er de fleste veje på Manhattan i New York enten nord-syd eller øst-vest, så man kan ikke bare gå eller køre "på skrå", men kun lodret eller vandret.

Hvis vi ser på punkterne \(P(2,3)\) og \(Q(5,7)\), så er den almindelige afstand \(5\) ved hjælp af Pythagoras, mens Manhattan-afstanden er \(3+4=7\). Dette er illustreret på figur 3.

Figur 3: Den almindelige afstand mellem punkterne \(P(2,3)\) og \(Q(5,7)\) er \(5\), mens Manhattan-afstanden er \(7\).
NoteOpgave 7

  • Indtegn punkterne \(A(1,7)\), \(B(3,4)\) og \(C(5,6)\) i et koordinatsystem.

  • Udregn både almindelig afstand og Manhattan-afstand mellem hvert par af punkter.

NoteOpgave 8

I eksemplet og i opgave 7 var Manhattan-afstanden større end den almindelige afstand, men kan Manhattan-afstanden være mindre end den almindelige afstand eller kan de to afstande være ens?

NoteOpgave 9

Se på figur 4 herunder fra opgave 2 igen.

Punkterne inde i cirklen har en almindelig afstand på under \(10\) til det grå punkt, men hvilke af punkterne har mon en Manhattan-afstand på under \(10\) til det grå punkt?

  • Overvej, hvordan punkter med en Manhattan-afstand på præcis \(10\) til det grå punkt ligger (måske er du nødt til at tegne lidt)?

  • Den almindelige afstand giver en cirkel med det grå punkt i centrum, men hvilken figur giver Manhattan-afstanden omkring det grå punkt?

  • Hvilken farve bør det grå punkt derfor have, hvis Manhattan-afstanden benyttes? Giver det samme resultatet, som du fik i opgave 2?

Figur 4: Koordinatsystem med \(31\) punkter, samt en cirkel med radius \(10\) omkring det grå punkt \(P(15,15)\)
NoteOpgave 10

Opstil en formel for den almindelige afstand mellem to punkter med koordinaterne \((x_1, y_1)\) og \((x_2, y_2)\). Det er en formel, du kender i forvejen.

Opstil tilsvarende en formel for Manhattan-afstanden. Det er nok ikke en formel, du har set før.

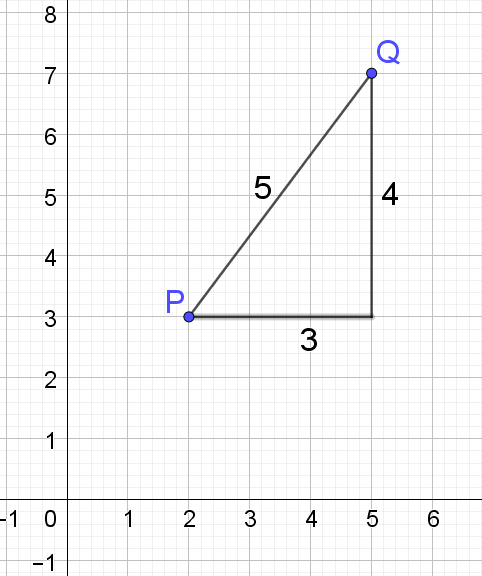
Du kan læse mere om Manhattan-afstanden her.

Hvilken politiker er du mest enig med?

Op til både folketings-, kommunal- og regionalvalg kan man svare på en række spørgsmål, hvorefter ens svar bliver sammenlignet med politikernes svar på de samme spørgsmål. Herefter kan man så se, hvem man er mest enig med.

Her er et eksempel fra kommunalvalget i 2025: Tag kandidattesten Kommunalvalg 2025 - Altinget - Alt om politik: altinget.dk.

NoteOpgave 11
  • Klik på linket ovenfor, vælg din egen kommune i testen og besvar spørgsmålene. Se derefter, hvem du ifølge kandidattesten er mest enige med, og hvor mange procent enige I er. Klik også på "Sammenlign svar", hvor du i detaljer kan se, hvor I er enig eller uenige.

Men hvordan virker det mon? Hvordan vurderes, hvilken kandidat du er mest enig med, og hvordan udregnes, hvor mange procent enige I er?

Til hvert spørgsmål kan der svares "helt uenig", "uenig", "enig" eller "helt enig", men desuden er der en skjult "neutral" mulighed i midten, som man ikke kan vælge:

Helt uenig Uenig Neutral Enig Helt enig

Afstanden mellem to svar regnes som antal "felter" i tabellen, så afstanden mellem "Uenig" og "Enig" er \(2\), mens afstanden mellem "Enig" og "Helt enig" er \(1\), og den største afstand er \(4\).

I figur 5 ses en persons svar og et partis kandidaters svar på \(23\) spørgsmål. Opstillingen på figuren er lidt anderledes end på Altinget for at gøre det mere overskueligt, men indholdet er tilsvarende. Bemærk, at antallet af spørgsmål kan variere fra kommune til kommune, så du har måske færre eller flere spørgsmål.

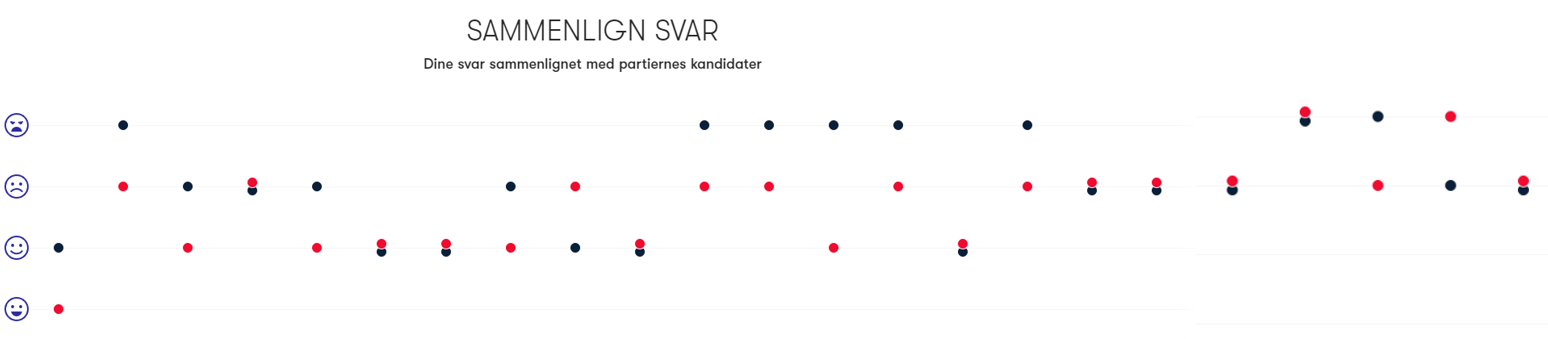
Figur 5: En persons svar (sort) og et partis kandidaters svar (rød) på \(23\) spørgsmål.

Afstanden i det første spørgsmål er \(1\), afstanden i det andet spørgsmål også \(1\) og afstanden i det tredje spørgsmål er \(2\) på grund af den skjulte "neutral" mulighed i midten.

NoteOpgave 12

  • De 3 første afstande er altså 1, 1 og 2. Udregn afstanden for hver af de øvrige \(20\) spørgsmål.

  • Læg så afstandene sammen, hvilket svarer til en form for Manhattan-afstand, da afstanden regnes for hvert enkelt spørgsmål for sig. Hvilken samlet afstand giver det?

NoteOpgave 13

  • Hvad er den mindst mulig samlede afstand for de \(23\) spørgsmål? Hvordan skal svarene for partiet og for vælgeren se ud fra at få denne afstand?

  • Hvad er den størst mulige afstand, og hvordan skal svarene så se ud?

NoteOpgave 14

Vend tilbage til dine egne svar på testen.

Beregn afstand i forhold til den kandidat, du var mest enig med, og den kandidat, du var mest uenig med.

For hver kandidat viser siden, hvor mange procent I er enige. Overvej, hvordan denne procent er regnet ud - tænk på afstanden som "hvor uenige I er" - og brug det til at regne en procent for "enighed".

Passer dine udregninger med sidens procenter?

Delvis facitliste

Facitliste.