Lever du bæredygtigt?
Formål
Vi skal i dette forløb snuse til, hvad kunstig intelligens er for noget. Vi tager udgangspunkt i lineære funktioner af både én og to variable. Dernæst skal vi se på, hvordan man finder toppunktet for en parabel med en såkaldt iterativ metode. Herefter skal vi se, hvordan denne metode kan bruges til at finde bedste rette linje. Endelig slutter vi af med at træne et simpelt kunstigt neuralt netværk i et eksempel, som handler om at kunne forudsige, om en person lever bæredygtigt eller ej baseret på svarene på en række spørgsmål.
Funktioner
Vi starter med at se på funktioner, som vi kender dem.
Et taxafirma – lad os kalde det "Taxa1" – tager \(10\) kroner for hver kørt kilometer. Prisens afhængighed af afstanden kan så beskrives med formlen: \[ \textrm{Pris} = \textrm{Afstand} \cdot 10 \] hvor afstanden måles i kilometer, og prisen fås i kroner. Situationen kan illustreres, som vist i figur 1.
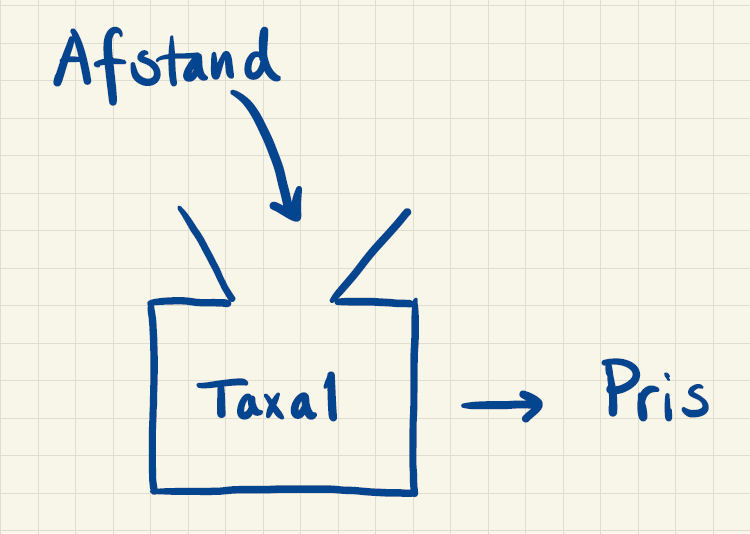
Et andet taxafirma – lad os kalde det "Taxa2" – tager kun \(5\) kroner for hver kørt kilometer, men tager så desuden \(3\) kroner for hvert minut turen tager. Prisens afhængighed af både afstand og tid kan så beskrives med formlen: \[ \textrm{Pris} = \textrm{Afstand} \cdot 5 + \textrm{Tid} \cdot 3 \] hvor afstanden måles i kilometer, tiden måles i minutter og prisen fås i kroner. Det kan illusteres sådan her:
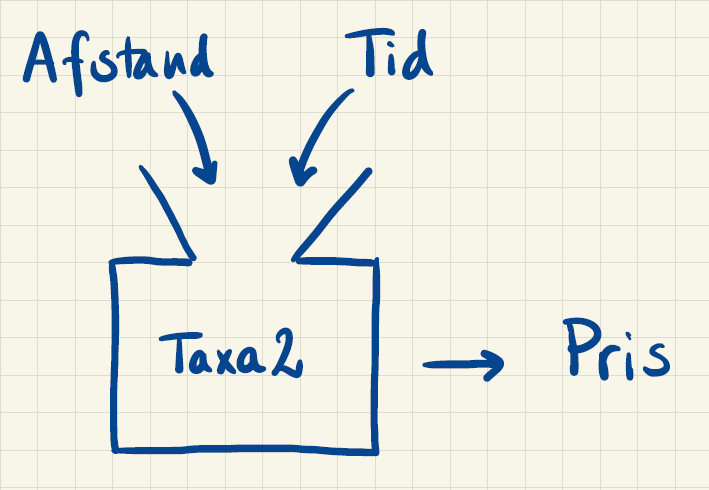
Det brugte input kaldes de uafhængige variable, det beregnede output kaldes den afhængige variabel og sammenhængen, der beskriver, hvordan output afhænger af input, kalder vi en funktion.
For "Taxa1" er prisen en funktion af én variabel – afstanden – og tallet \(10\) er en parameter, der bruges til at fastlægge funktionen.
For "Taxa2" er prisen en funktion af to variable – afstand og tid – og tallene \(3\) og \(5\) er parametre, der bruges til at fastlægge funktionen.
Neurale net
Inden for kunstig intelligens får man brug for nogle mere komplicerede funktioner, end dem vi så i taxaeksemplet, nemlig de såkaldte kunstige neurale net. Et kunstigt neuralt net forsøger at efterligne hjernen med et antal hjerneceller (neuroner) og forbindelser mellem dem. Man kan illustrere det således:
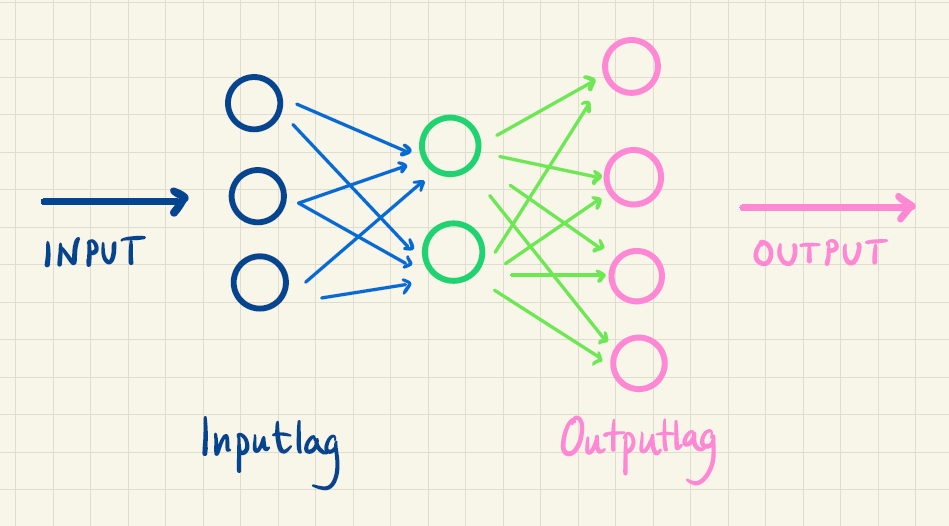
Idéen er, at man sender nogle inputvariable ind i nettet (vist som de mørkeblå cirkler til venstre i figur 3), hvor der sker nogle beregninger (de grønne cirkler i midten). Herefter returnerer netværket én eller flere outputværdier (vist som de lyserøde cirkler til højre).
Det kan være meget mere kompliceret, end det vi har vist i figur 3 – med mange flere knudepunkter i mange lag og med mange forbindelser.
Uanset om input er tal, tekster, billeder, film eller andet, så bliver det altid oversat til et antal tal, så der kan sendes et tal til hvert knudepunkt i inputlaget.
Alle forbindelserne har tilknyttet en parameter (også kaldet en vægt), som bliver ganget på tallet, inden det bliver sendt videre. Det samlede input til et knudepunkt er i det mest simple tilfælde summen af de sendte bidrag fra knudepunkterne i laget før1.
1 Ofte anvender man også en såkaldt aktiveringsfunktion. Det kan du læse mere om her.
Til sidst ender man med et tal i hvert knudepunkt i outputlaget, som så kan oversættes tilbage til tal, tekster, billeder, film eller andet.
Bemærk, at alle vægtene knyttet til forbindelserne mellem knudepunkterne fastlægger den funktion, som beskriver hvordan output afhænger af input.
Vi kan illustrere funktionen fra "Taxa2" med samme billede, hvor en konkret taxatur bliver oversat til to tal: afstand og tid. Det er vist i figur 4.
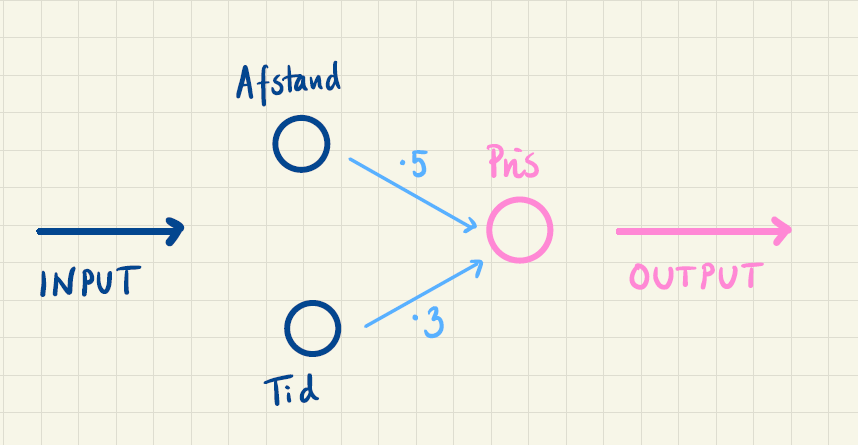
For at få et velfungerende neuralt net skal man altså forsøge at vælge disse vægte, så man får det ønskede output. Det gøres i en iterativ proces, hvor man gradvist træner det neurale net ved hjælp af store mængder træningsdata.
De næste to eksempler Toppunkt for en parabel og Bedste rette linje skal illustrere metoderne bag den iterative proces, der bruges til at træne neurale net.
Det man gør, når man træner et neuralt net til et datasæt, svarer til det, man gør, når man finder bedste rette linje for et sæt af datapunkter. I afsnittet Bedste rette linje ser vi, hvordan den iterative metode virker i dette tilfælde. Inden da forklares den iterative metode i afsnittet Toppunkt for en parabel.
Toppunkt for en parabel
Formålet i det første eksempel her er at finde gode tilnærmede bud til \(x\)-koordinaten i toppunktet for en parabel. Det er her en vigtig pointe, at vi ikke bruger de eksakte formler, der jo faktisk findes. På den måde kan vi illustrere den iterative proces i et tilfælde, hvor vi kender den eksakte løsning.
Grafen for et andengradspolynomium er en parabel, og hvis tallet foran \(x^2\) er positivt, vender grenene opad. Toppunktets \(x\)-værdi er derfor den \(x\)-værdi (\(x_T\)), der giver den mindst mulige \(y\)-værdi (\(y_T\)). Se figur 5.
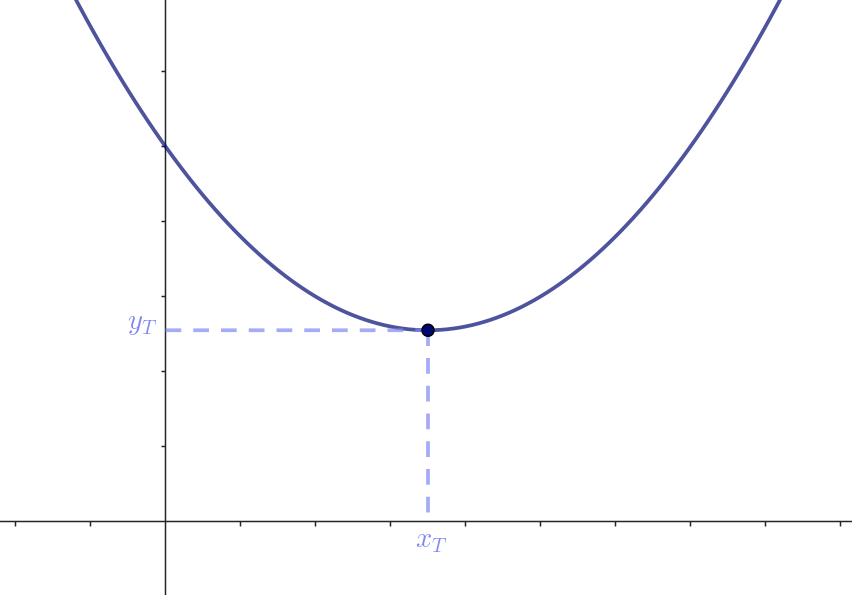
Når vi ønsker at finde toppunktets \(x\)-værdi med en iterativ proces, vil vi tænke på parablen som en bakke, hvor vi ønsker at komme ned i bunden af bakken til minimum. Det kan vi gøre på følgende måde:
Vælg en tilfældig \(x\)-værdi (\(x_{start}\)) og udregn den tilhørende \(y\)-værdi (\(y_{start}\)) – det svarer til, at vi stiller os et tilfældigt sted på bakken.
Det er næppe den rigtige \(x\)-værdi for toppunktet, men vi kan komme tættere på den rigtige værdi ved enten at skrue lidt op for \(x\) eller lidt ned for \(x\) for at gå ned ad bakken mod minimum.
Vi afgør om vi skal skrue op eller ned for \(x\) ved at udregne en \(y\)-værdi (\(y_{ny}\)) for en \(x\)-værdi (\(x_{ny}\)), der er lidt større end den valgte, og sammenligne den med \(y_{start}\).
Får vi en større \(y\)-værdi, så er vi på vej væk fra minimum, og vi skal derfor skrue lidt ned for \(x\). Se figur 6.
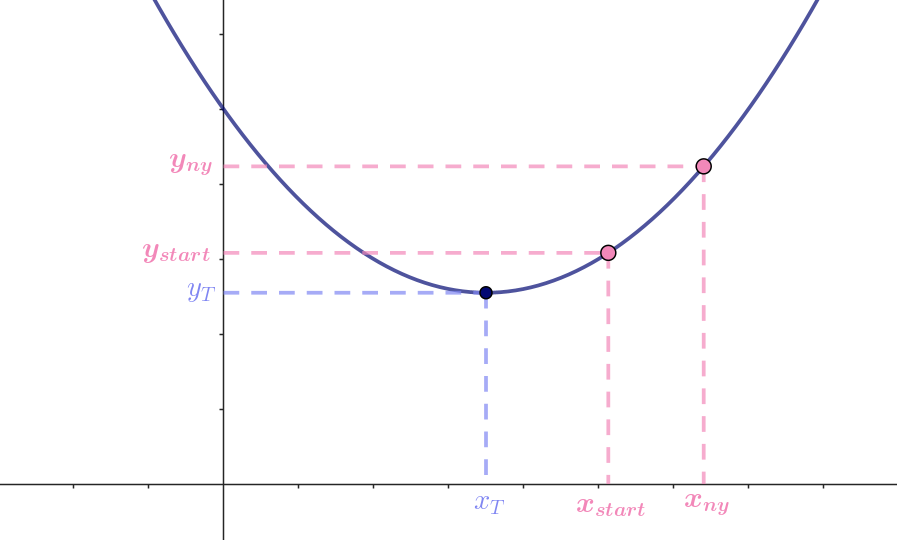
- Får vi en mindre \(y\)-værdi, så er vi på vej hen mod minimum, og vi skal derfor skrue lidt op for \(x\). Se figur 7.
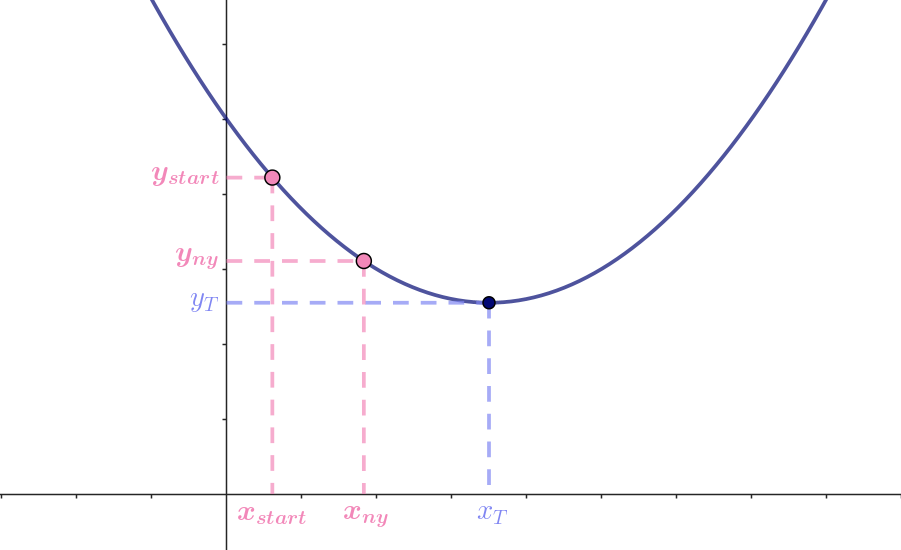
Vi gentager nu processen indtil en tilfredsstillende præcision er opnået. Vi kan vælge at tage mindre skridt, når vi tror, at vi er tæt på toppunktet. Det kan vi se, når de to beregnede \(y\)-værdier er ret ens.
Lad os se på et eksempel.
Eksempel 1: Iterativ bestemmelse af toppunkt
Vi ser på andengradspolynomiet med forskrift
\[ f(x)=2x^2-20x+55 \] Vi starter med at gætte på en \(x\)-værdi på \(4\):
\[ x_{start} = 4 \] Vi skruer lidt op for \(x\)-værdien:
\[ x_{ny} = 4.2 \]
Den størrelse, som vi lader \(x\)-værdien vokse med, kaldes for skridtlængden. Her har vi altså valgt en skridtlængde på \(0.2\).
Vi beregner funktionsværdier:
\[ \begin{aligned} f(4) &= 7 \\ f(4.2) &= 6.28 \end{aligned} \]
Da \(y\)-værdien er blevet mindre ved at skrue op for \(x\), vælger vi at skrue op for \(x\). Vi sætter derfor
\[ \begin{aligned} x_{start} &= 4.2 \\ x_{ny} &= 4.4 \end{aligned} \]
og udregner funktionsværdier
\[ \begin{aligned} f(4.2) &= 6.28 \\ f(4.4) &= 5.72 \\ \end{aligned} \]
Da \(y\)-værdien igen er blevet mindre ved at skrue op for \(x\), vælger vi at skrue op for \(x\).
Sådan fortsætter vi med enten af skrue op eller ned for \(x\), indtil de to beregnede funktionsværdier er ret ens.
Bedste rette linje
I dette eksempel vil vi finde tallene \(a\) og \(b\) for den bedste rette linje \(y=ax+b\). Det er igen her en vigtig pointe, at vi ikke bruger de eksakte formler, der jo faktisk findes. På den måde kan vi igen illustrere den iterative proces i et tilfælde, hvor vi kender den eksakte løsning.
Når vi laver lineær regression, finder vi den rette linje, som "bedst" beskriver en række målepunkter. Vi skal her starte med at se nærmere på, hvad vi egentlig mener med "bedst".
Vi forestiller os en måleserie bestående af fem punkter:
| \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(x_5\) |
|---|---|---|---|---|
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | \(y_5\) |
I figur 8 har vi indtegnet et eksempel på sådanne fem punkter og en ret linje med ligning
\[ y = ax + b \]
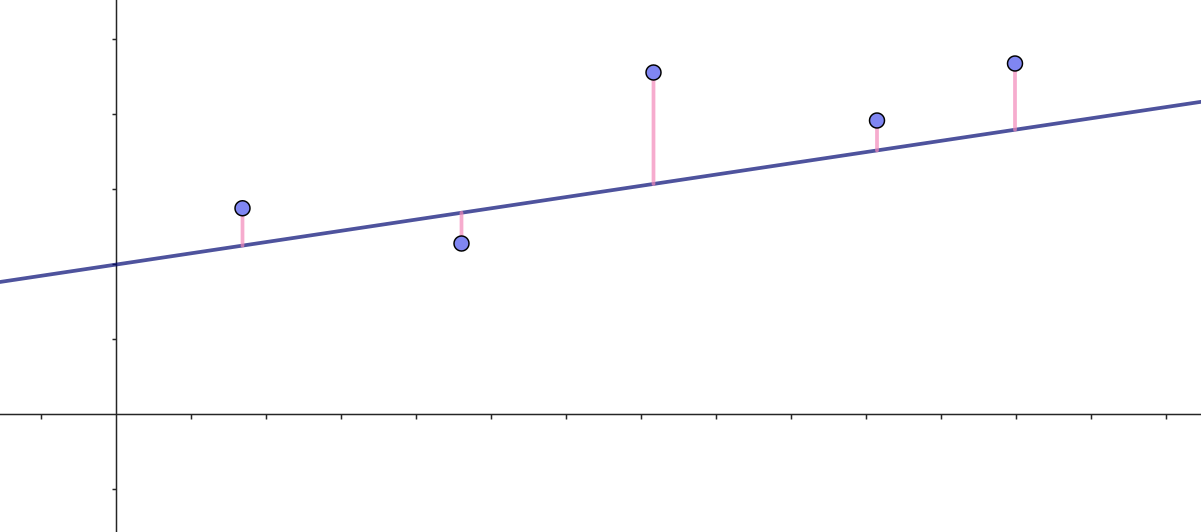
Desuden har vi indtegnet den lodrette afstand fra hvert af de fem punkter ned til linjen. Afstanden \(r_1\) fra det første punkt \((x_1,y_1)\) ned til linjen beregnes sådan her:
\[ r_1 = y_1 - (ax_1+b) \]
På tilsvarende vis beregnes de andre afstande.
I princippet vil vi gerne finde den rette linje, hvor alle disse afstande til sammen er så lille som mulig. Nu vil det bare være sådan, at hvis punktet ligger over linjen, så vil afstanden være positiv, mens hvis punkterne ligger under linjen, så vil afstanden være negativ. Man kan derfor ikke bare lægge alle afstandene sammen, fordi man kan ende på en sum, som er tæt på \(0\) uden, at linjen måske er specielt god. For at slippe af med de negative afstande sætter man alle afstande i anden og ser derfor på den kvadrerede sum:
\[ r_1^2 + r_2^2 + r_3^2 + r_4^2 + r_5^2 \]
På figur 9 er denne kvadratsum illustreret. Hvis man ellers har de samme enheder på akserne, vil hver af de fem kvadrerede afstande svare til arealet af de kvadrater, som er indtegnet på figuren. Den bedste rette linje er så den linje, som minimerer det samlede areal af kvadraterne.
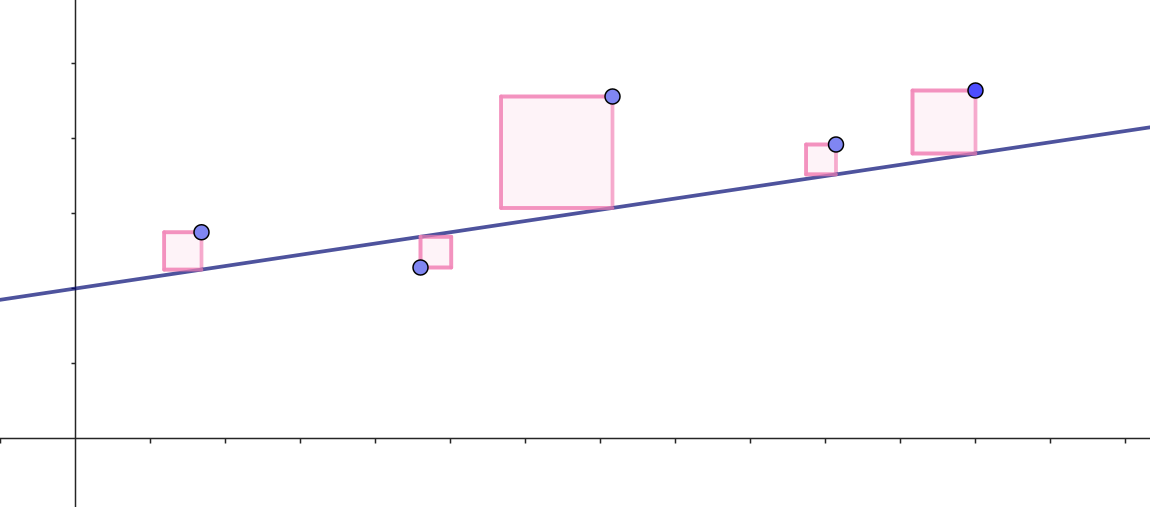
I den interaktive figur herunder kan du selv prøve at ændre på værdien af \(a\) og \(b\) og se, om du kan få kvadratsummen mindre.
Kalder vi summen af arealerne af kvadraterne for fejlen hørende til en given linje, så vil fejlen altså afhænge af tallene \(a\) og \(b\), som du lige har set.
Lad os se på et konkret eksempel:
Eksempel 2: Fejlen hørende til en linje
Vi ser på følgende måleserie med fem punkter:
| \(1\) | \(3\) | \(4\) | \(6\) | \(9\) |
|---|---|---|---|---|
| \(5\) | \(7\) | \(8\) | \(11\) | \(15\) |
I figur 10 er punkterne indtegnet sammen med linjen med ligning \(y=2x+1\).
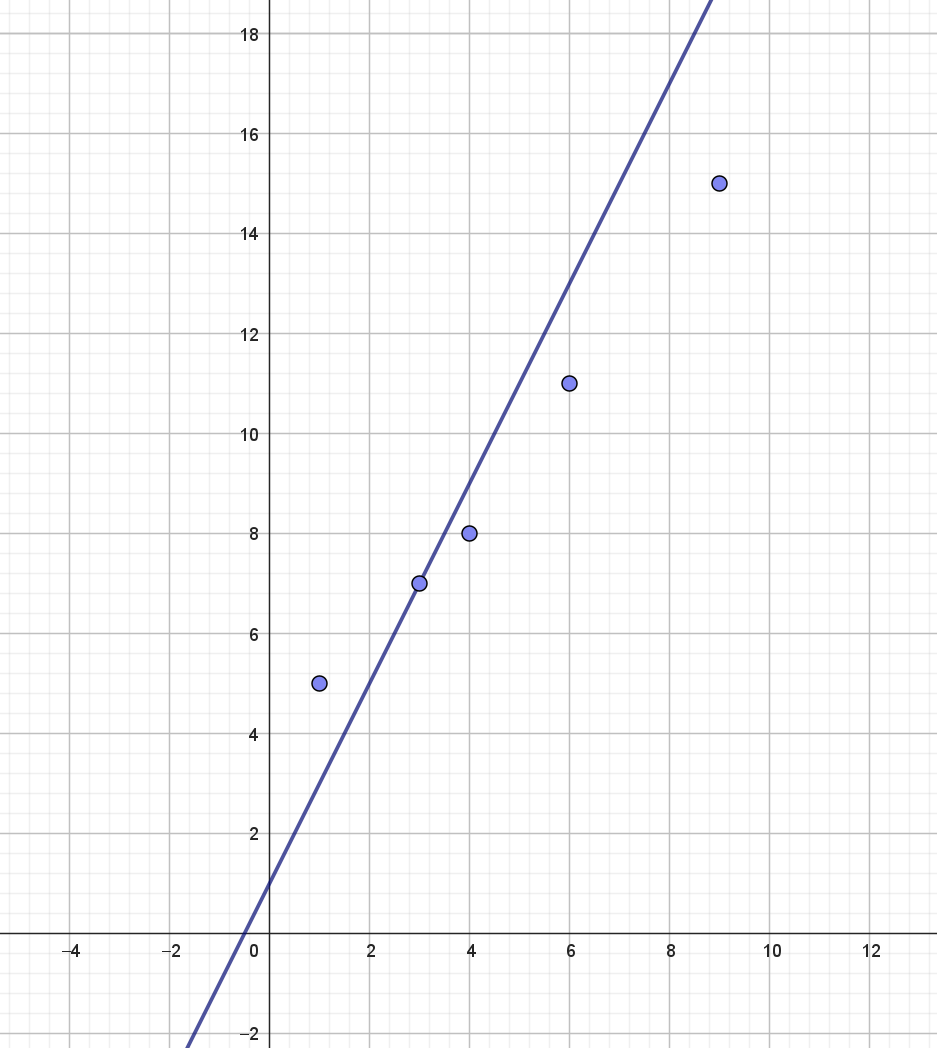
Fejlen hørende til denne linje er
\[ \begin{aligned} &(y_1-(2 \cdot x_1 +1))^2 + (y_2-(2 \cdot x_2+1))^2 + \\ &(y_3-(2 \cdot x_3+1))^2 + (y_4-(2 \cdot x_4+1))^2 + \\ &(y_5-(2 \cdot x_5+1))^2 = 25 \end{aligned} \]
hvor vi har indsat \(x\)- og \(y\)-værdierne for måleserien.
Opskriver vi fejlen helt generelt, fås \[ \begin{aligned} \textrm{fejl}(a,b) = &(y_1-(a \cdot x_1 +b))^2 + \\ &(y_2-(a \cdot x_2+b))^2 + \\ &(y_3-(a \cdot x_3+b))^2 + \\ &(y_4-(a \cdot x_4+b))^2 + \\ &(y_5-(a \cdot x_5+b))^2 \end{aligned} \]
Indsættes \(x\)- og \(y\)-værdierne fra måleserien og reduceres der, får vi:
\[ \textrm{fejl}(a,b) = 143 a^2 + 46 ab + 5b^2 -518a-92b+484 \tag{1}\]
Så kan fejlen hørende til linjen \(y=2x+1\) udtrykkes som funktionsværdien
\[ \textrm{fejl}(2,1) = 25. \]
Vi skal finde minimumspunktet for funktionen \(\textrm{fejl}(a,b)\). Det vil sige, de to tal \(a\) og \(b\), som gør fejlen mindst mulig. Den bedste rette linje er så \(y=ax+b\). Vi finder $a $ og \(b\) med en iterativ procedure som i afsnittet Toppunkt for en parabel.
Vi kan starte således:
Startgæt \(a=2\) og \(b=1\), hvor fejlen er:
\[\textrm{fejl}(2,1) = 25\]
Skrue på \(a\)-værdien
Vi prøver at skrue op for \(a\):
\[\textrm{fejl}(2.2,1) = 50.72\]
Fejlen voksede ved at skrue op for \(a\), så vi vælger i stedet at skrue ned:
\[\textrm{fejl}(1.8,1) = 10.72\]
Vi kan nu se, at det gav en mindre fejl – det vil sige en bedre linje.
Det nye gæt er nu \(a=1.8\) og \(b=1\), hvor fejlen er:
\[\textrm{fejl}(1.8,1) = 10.72\]
Skrue på \(b\)-værdien
Vi prøver at skrue op for \(b\):
\[\textrm{fejl}(1.8,1.2) = 11.08\]
Fejlen voksede ved at skrue op for \(b\), men kun ganske lidt. Vi kan så vælge, at lade \(b\)-værdien være uændret eller bare skrue lidt ned for \(b\):
\[\textrm{fejl}(1.8,0.8) = 10.76\] \[\textrm{fejl}(1.8,0.9) = 10.69\]
Det nye gæt er nu \(a=1.8\) og \(b=0.9\), hvor fejlen er:
\[\textrm{fejl}(1.8,0.9) = 10.69\] På den måde kan man fortsætte.
Det er vigtigt, at man skiftevis justerer \(a\) og \(b\). Man kan ikke gøre den ene færdig først. Man vil ofte se, at den ene måske falder i starten, men når den anden så er justeret nogle gange, så begynder den måske at stige igen.
Træning af neurale net
De to eksempler Toppunkt for en parabel og Bedste rette linje illustrerer, hvordan man med en iterativ proces kan bestemme parametrene \(a\) og \(b\) for den bedste rette linje. Overordnet set er det den samme metode, der bruges til at træne neurale net, blot har man mange flere parametre, så det kræver meget regnekraft.
I afsnittet Neurale net så vi, at alle parametrene knyttet til forbindelserne mellem knudepunkterne i et neuralt net fastlægger den funktion, som beskriver hvordan output afhænger af input. For at få et velfungerende neuralt net skal man forsøge at vælge disse parametre, så man får det ønskede output. Det gøres på følgende måde:
Man skal have adgang til store mængder træningsdata, hvor man kender både input og det ønskede output. Man definerer så en fejlfunktion, som kan beskrive afvigelsen mellem de faktiske output fra det neurale net og de kendte ønskede output. Parametrene vælges, så denne fejl bliver mindst mulig.
Vælg en startværdi for alle parametrene i det neurale net. Herefter justerer man gradvist på alle parametrene ved at forsøge at gøre fejlen lidt mindre ved hver justering. Det fortsætter man med, indtil fejlen forhåbentlig stabiliserer sig.
Til sidst har man brug for noget testdata, som ikke er brugt til træningen af det neurale net, men hvor man også kender både input og det ønskede output. Det bruges til at afprøve, om det neurale net fungerer efter hensigten ved at teste, om det neurale net kan forudsige output i testedata.
Anvendelse: Lever du bæredygtigt?
Vi vil lave en primitiv test baseret på kunstig intelligens og et neuralt netværk, men først skal vi have indsamlet noget træningsdata og testdata.
 Udgangspunktet er et spørgeskema med fire spørgsmål omhandlende aspekter af bæredygtighed, hver med fem svarmuligheder. Vi tildeler hver svarmulighed et pointtal, for eksempel -2, -1, 0, 1 og 2.
Udgangspunktet er et spørgeskema med fire spørgsmål omhandlende aspekter af bæredygtighed, hver med fem svarmuligheder. Vi tildeler hver svarmulighed et pointtal, for eksempel -2, -1, 0, 1 og 2.
Et eksempel på et spørgsmål kunne være:
"Hvor ofte cykler du?"
med følgende valgmuligheder (sæt et kryds):
| Aldrig | Få gange om året | Få gange om måneden | Få gange om ugen | Dagligt |
|---|---|---|---|---|
| X |
Den, der besvarer spørgeskemaet, ser det ikke, men vi oversætter svarene til pointtal:
| Aldrig | Få gange om året | Få gange om måneden | Få gange om ugen | Dagligt |
|---|---|---|---|---|
| -2 | -1 | 0 | 1 | 2 |
En besvarelse af spørgeskemaet giver et tal knyttet til svaret på hvert spørgsmål.
Som træningsdata lader vi et antal personer, som vi på forhånd ved enten prøver at leve bæredygtigt eller er ligeglade, besvare spørgeskemaet. Hvis man prøver at leve bæredygtigt, tildeles man resultatet 1, og ellers tildeles man resultatet 0.
Herunder er et eksempel på et opnået sæt træningsdata skrevet ind i Excel (du kan hente Excel-filen her):
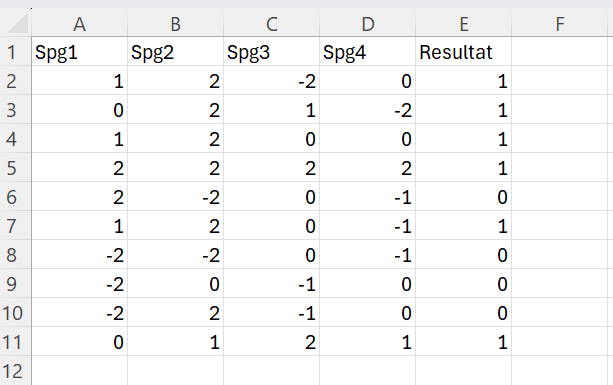
Vi vil nu bruge ovenstående træningsdata til at træne et neuralt net til at afgøre ud fra svarene på spørgeskemaet, om man lever bæredygtigt eller ej.
Gå ind på Kunstig neuron app’en, hvor du kan uploade Excel-filen med træningsdata, træne et neuralt net og til sidst få oplyst de opnåede vægte, som er de parametre, der skal bruges i forbindelserne mellem knudepunkterne.
Gør følgende:
Klik i "Browse…" under fanen "Data" og find Excel-filen med træningsdata og indlæs den. Tryk på "Næste".
Vælg under fanen "Variable", at target-variablen er "Resultat" og sæt target-værdien til 1, som blot betyder, at vi kalder det at leve bæredygtigt for succes.
Vælg herefter de fire spørgsmål som feature-variable. Tryk på "Næste".
Under fanen "Træning" sættes "Antal iterationer" til 20000, mens der ikke ændres på resten. Tryk på "Kør modellen". Med vores eksempel på træningsdata giver det følgende resultat:
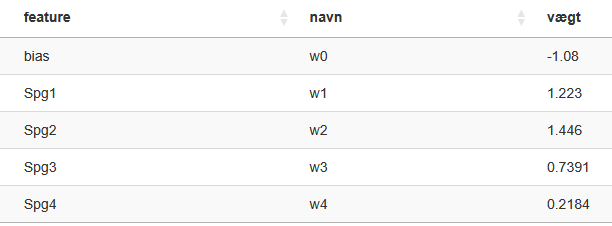
Grafen her (som findes til højre i app’en):
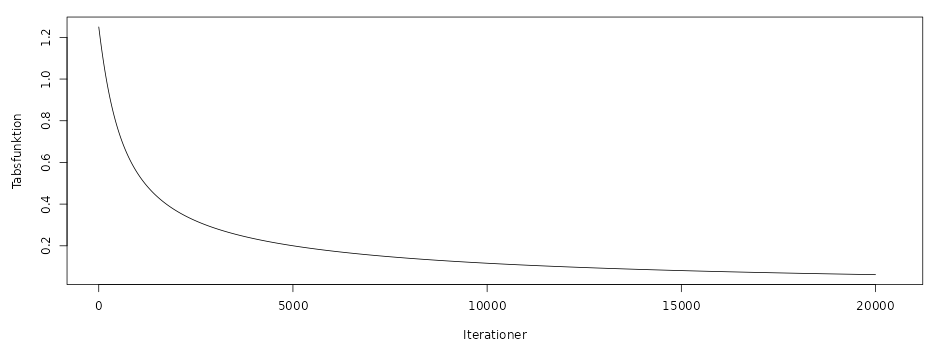
viser hvordan værdien af fejl-funktionen2 har ændret sig efter hver justering af vægtene. Vi kan her se, at fejl-funktionen har stabiliseret sig, som ønsket.
2 Fejl-funktionen kaldes også ofte for en "tabsfunktion" eller "loss function".
Med disse parametre kan vi nu lave en funktion, der ud fra svarene på spørgsmålene giver outputtet af det neurale net i form af enten tallet \(1\), hvis man lever bæredygtigt, eller tallet \(0\), hvis man ikke gør.
Funktionen kan illustreres således:
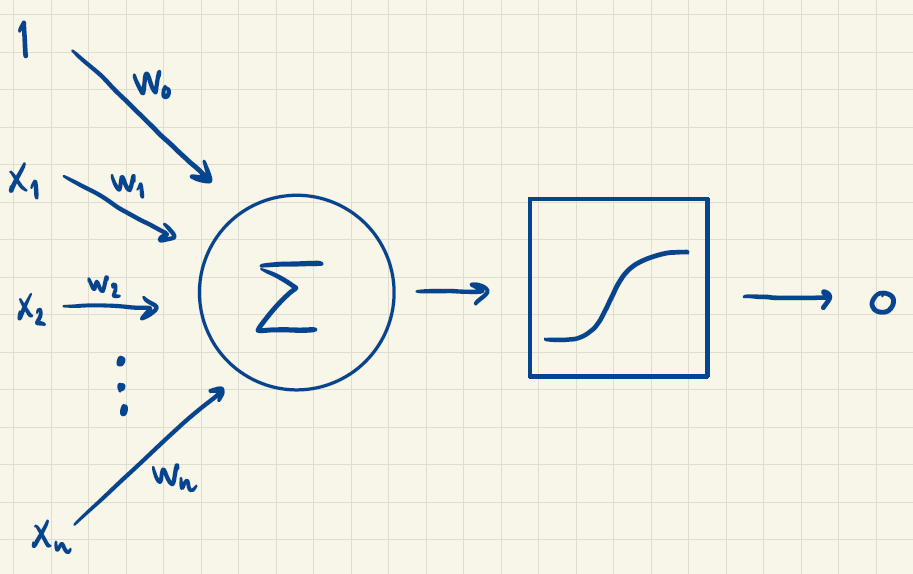
Her lader vi \(x_1\) være talværdien fra svaret på spørgsmål 1, \(x_2\) være talværdien fra svaret på spørgsmål 2 og så videre. Dem ganger man med vægtene \(W_1,\ldots,w_4\) fra det trænede neurale net og lægger sammen (og lægger vægten \(w_0\) til):
\[ w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 + w_4 \cdot x_4 \]
Til sidst konverterer man dette tal ved at bruge sigmoid-funktionen
\[ \sigma(x) = \frac{1}{1 + \mathrm{e}^{-x}} \] som ender med at give et tal mellem \(0\) og \(1\). Dette tal kan man tænke på som sandsynligheden for, om man er bæredygtig eller ej. Derfor vil man se på, om resultatet er større end \(0.5\). Hvis det er det, vil man sige at output er \(1\) (svarende til at være bæredygtig), mens man vil sætte output til \(0\), hvis resultatet er mindre end \(0.5\).
I eksemplet ovenfor er outputtet dermed givet ved en funktion af fire variable - fordi der var fire spørgsmål:
\[ \begin{aligned} f(x_1, x_2, x_3, x_4) = \sigma (w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 + w_4 \cdot x_4 ) = \\ \sigma (-1.08 + 1.223 \cdot x_1 + 1.446 \cdot x_2 + 0.7391 \cdot x_3 + 0.2184 \cdot x_4 ) \end{aligned} \]
For at afprøve om det trænede neurale net, og dermed formlen, virker, skal vi indsamle noget testdata på samme måde som træningsdata.
Som testdata lader vi altså et antal personer som vi på forhånd ved enten prøver at leve bæredygtigt eller er ligeglade besvare spørgeskemaet. Hvis man prøver at leve bæredygtigt, tildeles man resultatet \(1\), og ellers tildeles man resultatet \(0\).
Her er et eksempel på testdata indtastet i Excel:
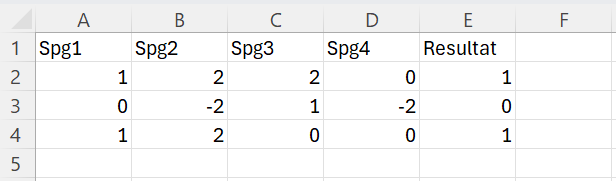
Vi kan nu se, om vi får det rigtige output:
\[ \begin{aligned} & f(1,2,2,0) \approx 0.989 > 0.5 \\\\ & f(0,-2,1,-2) \approx 0.025 < 0.5 \\\\ & f(1,2,0,0) \approx 0.954 > 0.5 \\\\ \end{aligned} \]
Outputtet bliver rigtigt i alle tre tilfælde.
Det ser altså ud til, at det trænede neurale net og dermed formlen kan bruges til at afgøre, om man lever bæredygtigt eller ej ud fra svarene på spørgsmålene i spørgeskemaet.
Du kan læse mere om kunstige neuroner her.
Brug af kunstig intelligens
Ulempen ved at bruge kunstig intelligens er, at fortolkningen af, hvad der foregår ved træningen af et neuralt net, og dermed også fortolkningen af svarene, er mere uklar i forhold til en simpel beregning.
Fordelen er, at man eventuelt kan løse problemer, der ikke kan løses på anden vis, blandt andet fordi man kan modellere mere komplicerede funktioner end de lineære. Det kræver dog, når man har adgang til store mængder træningsdata af en god kvalitet.