Opdatering af vægte i et simpelt neuralt netværk med to skjulte lag
Formål
Formålet med dette forløb er gennem detaljerede beregninger at forstå, hvordan vægtene i et simpelt neuralt netværk til klassifikation med to skjulte lag opdateres med brug af sigmoid som aktiveringsfunktion og gradientnedstigning med squared error som tabsfunktion.
Dette kan ses som et skridt på vejen til at forstå, hvordan vægtene opdateres i et generelt neuralt netværk.
Et meget lille datasæt
I neurale netværk er der ofte rigtige mange inputvariable (features), rigtigt mange vægte og rigtig mange træningsdata.
For bedre at forstå, hvordan vægtene opdateres i et neuralt netværk, vil vi her se på et meget lille eksempel, så det manuelt er muligt at lave opdateringen af vægtene.
Vi vil lave et netværk med 2 inputvariable (\(x_1\) og \(x_2\)), 1 neuron i det første skjulte lag (\(y\)), 1 neuron i det andet skjulte lag (\(z\)) og 1 neuron i outputlaget (\(o\)). Netværket er illustreret i figur 1.
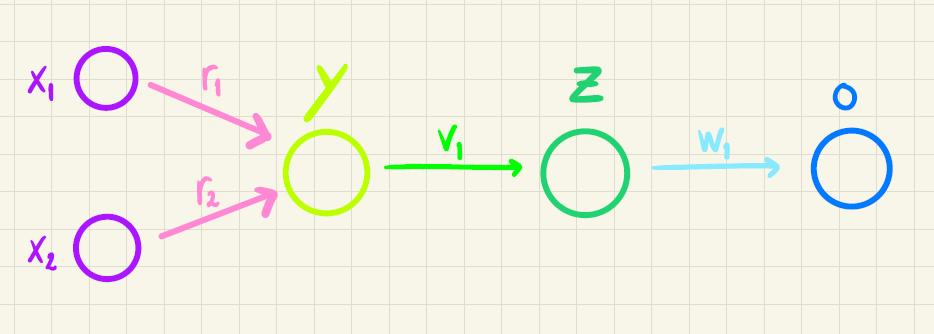
Konkret vil vi se på to features \(x_1\) og \(x_2\) og en targetværdi \(t\) ud fra følgende træningsdatasæt:
| \(x_1\) | \(x_2\) | \(t\) |
|---|---|---|
| 1 | 2 | 0 |
| 2 | 3 | 1 |
| 3 | 5 | 0 |
Vi vælger en learning rate på
\[\eta = 0.1,\]
sigmoid-funktionen som aktiveringsfunktion mellem lagene
\[\sigma(x)=\frac{1}{1+\mathrm{e}^{-x}}\] og squared error som tabsfunktion
\[E = \frac{1}{2} \sum_{m=1}^{M} \left (t^{(m)}-o^{(m)} \right)^2\]
Endeligt vælger vi alle startvægtene til at være \(0.5\), så \[ r_0=0.5 \textrm{ (bias)},\qquad r_1=0.5,\qquad r_2=0.5 \]
\[ v_0=0.5 \textrm{ (bias)}, \qquad v_1=0.5\]
\[ w_0=0.5 \textrm{ (bias)}, \qquad w_1=0.5 \]
Opdateringsregler
Fra noten om simple neurale netværk har vi opdateringsreglerne, som vi nu skal til at anvende på det konkrete træningsdatasæt.
Først udregnes feedforward-udtrykkene: \[ \begin{aligned} y^{(m)} &= \sigma (r_0 + r_1 \cdot x_1^{(m)} + r_2 \cdot x_2^{(m)} + \cdots + r_n \cdot x_n^{(m)}) \\ z^{(m)} &= \sigma (v_0 + v_1 \cdot y^{(m)}) \\ o^{(m)} &= \sigma(w_0 + w_1 \cdot z^{(m)}) \end{aligned} \] Herefter beregnes:
\[ \begin{aligned} \delta_w^{(m)} &= (t^{(m)}-o^{(m)} ) \cdot o^{(m)} \cdot (1-o^{(m)}) \\ \delta_v^{(m)} &= \delta_w^{(m)}\cdot w_1 \cdot z^{(m)} \cdot (1-z^{(m)}) \\ \delta_r^{(m)} &= \delta_v^{(m)} \cdot v_1 \cdot y^{(m)} \cdot (1-y^{(m)}) \end{aligned} \] Vægtene kan nu opdateres:
\(w\)-vægtene: \[ \begin{aligned} w_0^{\textrm{(ny)}} & \leftarrow w_0 + \eta \cdot \sum_{m=1}^{M} \delta_w^{(m)} \cdot 1\\ w_1^{\textrm{(ny)}} & \leftarrow w_1 + \eta \cdot \sum_{m=1}^{M} \delta_w^{(m)} \cdot z^{(m)}\\ \end{aligned} \]
\(v\)-vægtene: \[ \begin{aligned} v_0^{\textrm{(ny)}} & \leftarrow v_0 + \eta \cdot \sum_{m=1}^{M} \delta_v^{(m)}\cdot 1\\ v_1^{\textrm{(ny)}} & \leftarrow v_1 + \eta \cdot \sum_{m=1}^{M} \delta_v^{(m)}\cdot y^{(m)}\\ \end{aligned} \]
\(r\)-vægtene: \[ \begin{aligned} r_0^{\textrm{(ny)}} & \leftarrow r_0 + \eta \cdot \sum_{m=1}^M \delta_r^{(m)} \cdot 1 \\ r_1^{\textrm{(ny)}} & \leftarrow r_1 + \eta \cdot \sum_{m=1}^M \delta_r^{(m)} \cdot x_1^{(m)} \\ & \ \ \vdots & \\ r_n^{\textrm{(ny)}} & \leftarrow r_n + \eta \cdot \sum_{m=1}^M \delta_r^{(m)} \cdot x_n^{(m)} \end{aligned} \]
Beregninger
Et større datasæt
Det giver naturligvis ikke så meget mening med så lille et datasæt, og da slet ikke med blot én opdatering af vægtene. Lad os derfor se på et større datasæt, hvor vi laver mange iterationer med opdateringer, så vi kan se, om det neurale netværk reelt kan noget.
Lad os se, om vi kan få et neuralt netværk til at "opdage" følgende sammenhæng ud fra en lidt større mængde træningsdata.
Hvis \(4 < x_1 + x_2 < 7\) er targetværdien er \(1\), ellers er targetværdien \(0\). Det stemmer med det meget lille datasæt, vi indtil nu har anvendt.
I denne Excel-fil er der 200 linjer med træningsdata, som vi vil bruge til at træne et neutralt netværk med 2 skjulte lag. Men vi vil helt sikkert ikke selv lave opdateringerne af vægtene manuelt. I stedet vil vi bruge denne app.
Hvis du har lavet forløbet Skibidi toilet om vurdering af værdien af tabsfunktionen er for stor, kan du lave opgave 8. Ellers fortsæt med opgave 9.