Del 6: Maximum likelihood estimation

Forventet tid ca. 120 min.

Aktivitet 1

Start med at se denne video (eller læs afsnittet maksimum likelihood estimation):

Aktivitet 2

Fra afsnittet Maksimum likelihood estimation fandt vi frem til, at log-likelihoodfunktionen kan skrives på denne måde:

\[ \begin{aligned} l(a,b) =\sum_{i=1}^n\big( {y_i}\cdot \ln(p(x_i))+(1-y_i)\cdot \ln(1-p(x_i)) \big), \end{aligned} \tag{1}\]

hvor

\[ p(x_i) = \frac{ 1}{1 + e^{-(ax_i + b)}}=\frac{e^{ax_i + b}}{1+e^{ax_i +b}}. \tag{2}\]

Bestemmelse af $a$ og $b$ med Excels problemløser-værktøj

Vi vil nu finde estimater for $a$ og $b$ ved hjælp af Excel. Først og fremmest skal man sørge for, at man har aktiveret problemløser-værktøjet. Det gøres på følgende måde:

Gå op under filer og vælg indstillinger.
Vælg derefter tilføjelsesprogrammer.
Nederst vælges Excel-tilføjelsesprogrammer. Tryk på udfør.
Vælg til sidst tilføjelsesprogrammet problemløser fra en liste.

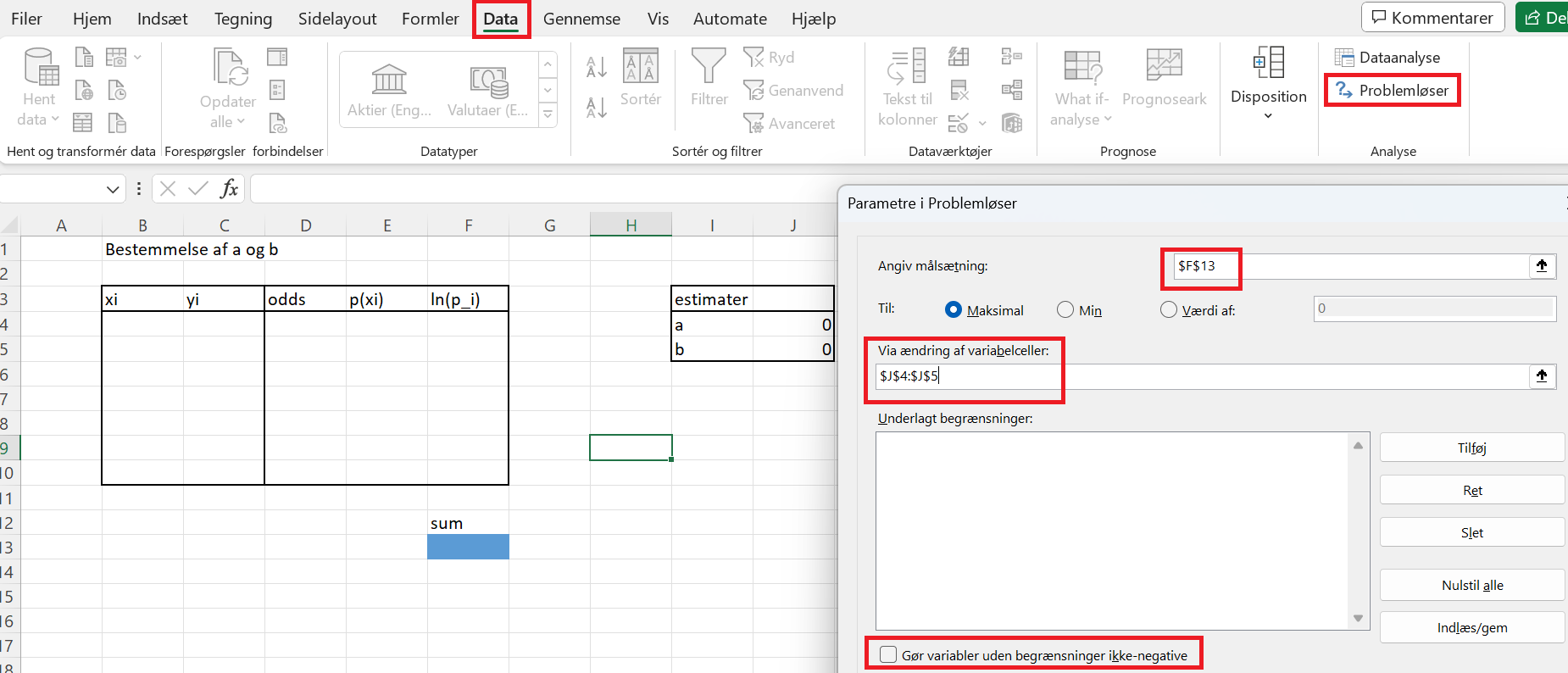
Illustration af Excel ark til bestemmelse af a og b samt brug af problemløser.

På billedet ses, hvordan man kan lave et lille regneark til at beregne de relevante størrelser. Der er lavet et par celler til de ukendte parametre $a$ og $b$, som med fordel kan sættes til 0 fra starten for at undgå numeriske problemer i Excel. Det oprindelige datasæt indsættes i søjlerne $x_i$ og $y_i$. I de næste søjler beregnes odds, $p(x_i)$ og $\ln(p_i)$ med formlerne¹ \[\begin{align*} odds &= e^{ax_i + b}\\ p(x_i) &= \frac{e^{ax_i + b}}{1+e^{ax_i +b}} = \frac{odds}{1+odds}\\ \ln(p_i)&= {y_i}\cdot \ln(p(x_i))+(1-y_i)\cdot \ln(1-p(x_i)). \end{align*}\]

¹ I Excel på dansk fås eksponentialfunktionen ved at skrive EKSP (og EXP i den engelske version). For at få den naturlige logaritmen skriver man LN i begge tilfælde.

Her er det vigtigt, at cellerne, der indeholder værdien af $a$ og $b$, benyttes når oddsene beregnes (det vil være smart med fastlåsning af referencerne, hvor man har $ foran både tal og bogstav ved reference). Til sidst finder man $l(a,b)$ i det blå felt ved at beregne summen af alle $\ln(p_i)$, som i formlen (1).

Nu mangler man bare at benytte problemløseren til at finde de værdier af $a$ og $b$, der gør værdien i det blå felt maksimal. På billedet er der vist med rød, hvor man finder problemløseren, og hvad der skal justeres. Målsætningen er den blå celle, der indeholder summen. Variabelcellerne er de to, der indeholder $a$ og $b$. Sørg for ikke at sætte flueben i boksen "Gør variabler uden begrænsninger ikke-negative". Tryk på løs.

Opgave 1

Antag, at vi har tre observationer nedenfor.

Opskriv et udtryk for likelihoodfunktionen $L(a,b)$.

$x$	1	2	3
$y$	1	1	0

En nyhedshjemmeside ønsker at målrette en biografreklame til brugerne. De har derfor registreret om 10 af hjemmesidens brugere har klikket på reklamen ($y=1$ hvis de har klikket, $y=0$ ellers) og hvor mange gange $x$, de har læst kulturnyheder den sidste måned. Datasættet er givet i nedenstående tabel. Firmaet bag hjemmesiden ønsker at modellere sandsynligheden $p(x)$ for at klikke på reklamen som funktion af $x$, så de kan målrette reklamen mod de brugere, der har størst sandsynlighed for at klikke på den.

Brug Excel til at finde $a$ og $b$.
Tegn grafen for $p(x)$.
Skal firmaet vælge at vise reklamen til brugere, der ofte eller sjældent læser kulturnyheder?

x	0	1	2	3	4	5	6	7	8	9
y	0	0	1	0	0	1	1	1	1	1

Opgave 2

Brug datasættet med de 2000 datapunkter og benyt problemløsning i Excel til at vise, at $a=0{,}022$ og $b=-3{,}9$ optimerer løsningen.

Aktivitet 1

Aktivitet 2

Bestemmelse af \(a\) og \(b\) med Excels problemløser-værktøj